计算几何——扫描线算法

计算几何——扫描线算法

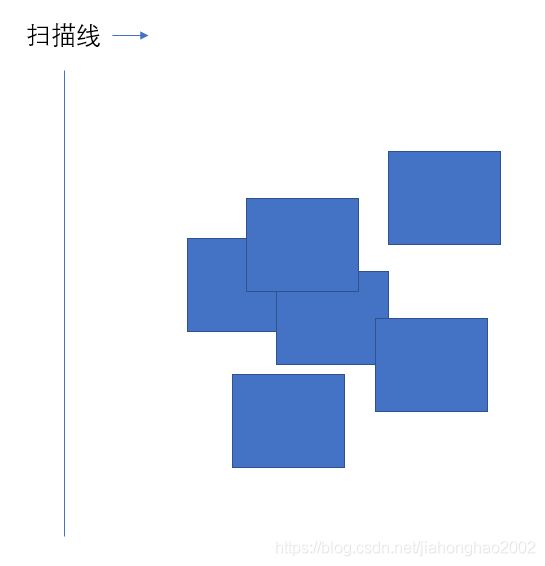
面对一个几何图形，计算机通过向某一个方向进行单线扫描，进行图形处理的方式叫做扫描线算法。

事件和事件处理程序

扫除线算法中最重要的就是对事件（Event）的处理。一个事件定义为当扫除线碰到点、边界、线等产生的进入或退出事件。

例如下图：

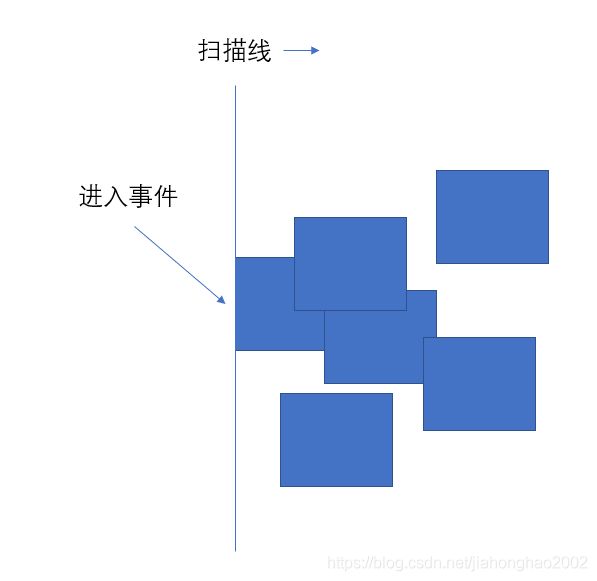
当扫描线碰到某一个矩形的左边界时将会产生一个进入事件，之后处理程序将对这个进入事件进行处理。

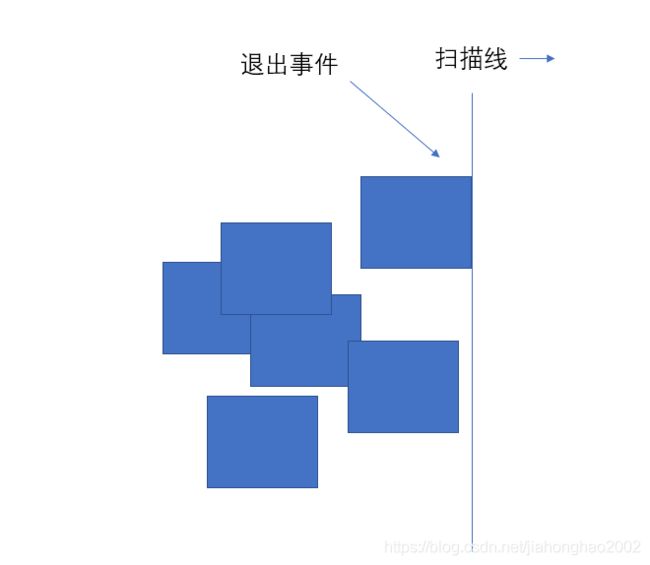
又或者当扫描线碰到某一个矩形的右边界时将会产生一个退出事件，之后处理程序将对这个退出事件进行处理。

一般的，我们将整个事件列表中的事件进行按照扫除线的扫描顺序进行排序，之后处理程序将会依次处理所有事件，而事件处理程序才是扫描线算法的核心。

天际线问题

LeetCode 218

the-skyline-problem

#include 

#define FR freopen("in.txt", "r", stdin)

typedef long long ll;
using namespace std;

struct Event
{
    int x;
    int height;
    bool start;
    bool operator<(const Event &o) const
    {
        if (x == o.x)
        {
            return height < o.height;
        }
        else
        {
            return x < o.x;
        }
    }
};

class Solution
{
public:
    vector<vector<int>> getSkyline(vector<vector<int>> &buildings)
    {
        // 构建事件列表
        vector<Event> events;

        for (vector<int> item : buildings)
        {
            events.push_back({item[0], item[2], true});
            events.push_back({item[1], item[2], false});
        }
        vector<vector<int>> ans;
        // 排序事件
        sort(events.begin(), events.end());
        multiset<int> heights;
        heights.insert(0);
        int maxHeight = 0;
        for (Event event : events)
        {
            if (event.start) // 如果是一个开始事件
            {
                heights.insert(event.height);
                if (event.height > maxHeight)
                {
                    maxHeight = event.height;
                    if (!ans.empty() && ans.back()[0] == event.x)
                        ans.pop_back();
                    vector<int> point;
                    point.push_back(event.x);
                    point.push_back(event.height);
                    ans.push_back(point);
                }
            }
            else // 否则为结束事件
            {
                heights.erase(heights.find(event.height));
                if (maxHeight == event.height)
                {
                    if (heights.count(event.height))
                    {
                        continue;
                    }
                    if (!ans.empty() && ans.back()[0] == event.x)
                        ans.pop_back();
                    maxHeight = *heights.rbegin();
                    vector<int> point;
                    point.push_back(event.x);
                    point.push_back(maxHeight);
                    ans.push_back(point);
                }
            }
        }

        return ans;
    }
};

相交面积问题

LeetCode 391

求出三个面积：

1. 极小包围矩形的面积
2. 所有矩形的面积和
3. 所有矩形组成的平面图形的面积

如果这三个面积相等返回True。

1和2是好处理的，3需要使用扫面线和线段树求解。

using ll = long long;

int LT(int x)
{
    return x << 1;
}
int RT(int x)
{
    return (x << 1) | 1;
}

struct Node
{
    ll len;
    int cnt;
    ll rlen;
};
struct Event
{
    ll x;
    int l;
    int r;
    bool enter;
};

vector<int> decre;

struct SegmentTree
{
    vector<Node> t;

    void buildTree(int i, int l, int r)
    {
        t[i].cnt = 0;
        t[i].len = 0;
        t[i].rlen = decre[r] - decre[l];
        if (l != r - 1)
        {
            int mid = (l + r) / 2;
            buildTree(LT(i), l, mid);
            buildTree(RT(i), mid, r);
        }
    }

    void cover(int i, int l, int r, int L, int R)
    {
        if (l >= R || r <= L)
            return;
        if (l >= L && r <= R)
        {
            t[i].cnt++;
            t[i].len = t[i].rlen;
            return;
        }
        int mid = (l + r) / 2;
        cover(LT(i), l, mid, L, R);
        cover(RT(i), mid, r, L, R);
        if (!t[i].cnt)
            t[i].len = t[LT(i)].len + t[RT(i)].len;
    }

    void uncover(int i, int l, int r, int L, int R)
    {
        if (l >= R || r <= L)
            return;
        if (l >= L && r <= R)
        {
            t[i].cnt--;
            if (!t[i].cnt)
                t[i].len = l == r - 1 ? 0 : t[LT(i)].len + t[RT(i)].len;
            return;
        }
        int mid = (l + r) / 2;
        uncover(LT(i), l, mid, L, R);
        uncover(RT(i), mid, r, L, R);
        if (!t[i].cnt)
            t[i].len = t[LT(i)].len + t[RT(i)].len;
    }

    ll getLen()
    {
        return t[1].len;
    }
};

class Solution
{
public:
    ll comb_area(vector<vector<int>> &rectangles)
    {
        for (vector<int> &r : rectangles)
        {
            decre.push_back(r[1]);
            decre.push_back(r[3]);
        }

        sort(decre.begin(), decre.end());
        decre.erase(unique(decre.begin(), decre.end()), decre.end());
        auto find_id = [&](int y) -> int
        {
            return lower_bound(decre.begin(), decre.end(), y) - decre.begin();
        };
        vector<Event> vec;

        for (vector<int> &r : rectangles)
        {
            vec.push_back((Event){r[0],
                                  find_id(r[1]),
                                  find_id(r[3]),
                                  true});
            vec.push_back((Event){r[2],
                                  find_id(r[1]),
                                  find_id(r[3]),
                                  false});
        }

        sort(vec.begin(), vec.end(), [](Event a, Event b)
             { return a.x < b.x; });

        SegmentTree st;
        st.t.resize(decre.size() * 4);
        int R = decre.size() - 1;
        st.buildTree(1, 0, R);
        ll lasx = vec[0].x;
        ll ans = 0;
        for (Event e : vec)
        {
            int x = e.x;
            int l = e.l;
            int r = e.r;
            bool enter = e.enter;
            if (x != lasx)
            {
                ans += st.getLen() * (x - lasx);
                lasx = x;
            }
            if (enter)
                st.cover(1, 0, R, l, r);
            else
                st.uncover(1, 0, R, l, r);
        }

        return ans;
    }
    bool isRectangleCover(vector<vector<int>> &rectangles)
    {
        vector<ll> bound(4);
        for (int i = 0; i < 4; i++)
        {
            bound[i] = (*min_element(rectangles.begin(), rectangles.end(), [&](const vector<int> &a, const vector<int> &b)
                                     {
                                         if (i <= 1)
                                             return a[i] < b[i];
                                         else
                                             return a[i] > b[i];
                                     }))[i];
        }

        ll area = abs(bound[0] - bound[2]) * abs(bound[1] - bound[3]);

        // 统计面积
        ll rarea = 0;
        for (vector<int> &r : rectangles)
            rarea += abs(0ll + r[0] - r[2]) * abs(0ll + r[1] - r[3]);

        ll carea = comb_area(rectangles);
        return area == rarea && area == carea;
    }
};