python之scipy.signal重采样
前言
在复现LiftingNet过程中,了解到作者对于不同转速设备的机械信号进行重采样来矫正转速,也就是固定长度的样本包含了相同旋转周期的设备信息,而非相同时间长度。po一下原文:

这里其实用到了阶次分析的原理,该样本长度对应的设备转过同样的角度,当然这里是针对不同稳定转速下的,阶比分析针对的是转速连续变化的信号,详情可参考大佬博客.
本文是探究python包中scipy.signal.resample的效果的,确切滴说是记录。
resample
这里是python关于resample函数的官方解释:https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.resample.html
该函数简单粗暴,也很适合我的需求,直接将原信号重采样到指定长度,scipy.signal.resample(x, num, t=None, axis=0, window=None, domain='time'),下面看一下代码和效果
import numpy as np
from scipy.signal import resample, resample_poly
import matplotlib.pyplot as plt
import scipy.fft as fft
x = np.linspace(0, 10, 600, endpoint=False)
y = np.cos(x**2/6.0*5)+np.cos(x*6.28*5)+np.sin(x**2*6.28*5)+np.random.normal(0, 1)*2
f = resample(y, len(x)//4)
xnew = np.linspace(0, 10, len(f), endpoint=False)
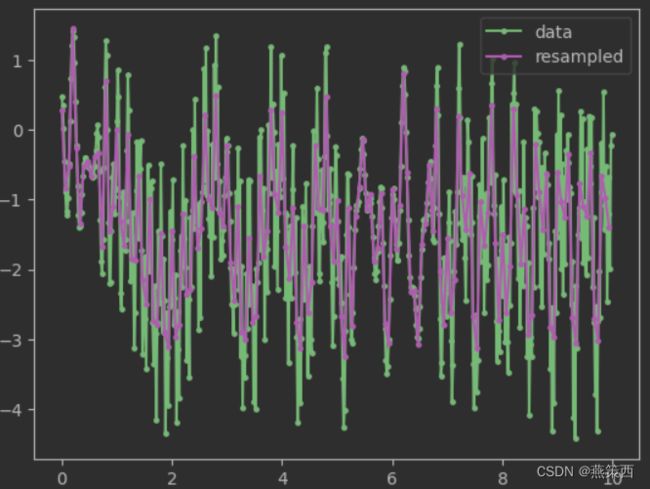
plt.plot(x, y, 'g.-', xnew, f, 'm.-', markersize=5)
plt.legend(['data', 'resampled'], loc='best')
plt.show()
fs = int(len(x) / (max(x)-min(x)))
wx = np.linspace(0, fs/2, len(x)//2+1)
fx = fft.fft(y).real[0:len(y) // 2 + 1]
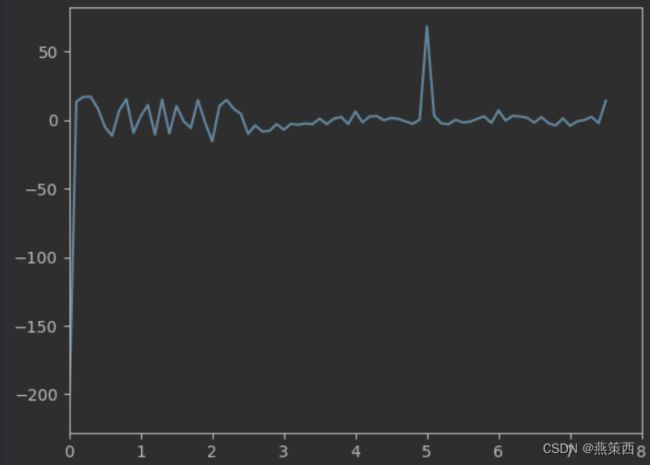
plt.plot(wx, fx)
plt.xlim([0, 8])
plt.figure()
fs = fs / 4
wx = np.linspace(0, fs/2, len(xnew)//2+1)
fx = fft.fft(f).real[0:len(f) // 2 + 1]
plt.plot(wx, fx)
plt.xlim([0, 8])
可以看到,该函数在对信号进行时域重采样的同时,保留了频域特征,没毛病。
resample_poly
这个函数的效果也跟上面一样,只是使用的方法原理有差异,官网介绍在:https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.resample_poly.html,它解释说比上面的操作略快,我没有实际测试,效果差不多。代码放这里,效果就不展示了,频域特征也保留了。scipy.signal.resample_poly(x, up, down, axis=0, window=('kaiser', 5.0), padtype='constant', cval=None)里面的up以及down分别填写目标采样率和当前信号采样率,或者采样点,都行。原论文里提到用的是MATLAB里面的resample函数,我也就使用了这个python里面对应的resample_poly了。
import matplotlib.pyplot as plt
import scipy.fft as fft
x = np.linspace(0, 10, 600, endpoint=False)
y = np.cos(x**2/6.0*5)+np.cos(x*6.28*5)+np.sin(x**2*6.28*5)+np.random.normal(0, 1)*2
f = resample_poly(y, len(x)//4, len(x))
xnew = np.linspace(0, 10, len(f), endpoint=False)
plt.plot(x, y, 'g.-', xnew, f, 'm.-', markersize=5)
plt.legend(['data', 'resampled'], loc='best')
plt.show()
fs = int(len(x) / (max(x)-min(x)))
wx = np.linspace(0, fs/2, len(x)//2+1)
fx = fft.fft(y).real[0:len(y) // 2 + 1]
plt.plot(wx, fx)
plt.xlim([0, 8])
plt.figure()
fs = fs / 4
wx = np.linspace(0, fs/2, len(xnew)//2+1)
fx = fft.fft(f).real[0:len(f) // 2 + 1]
plt.plot(wx, fx)
plt.xlim([0, 8])