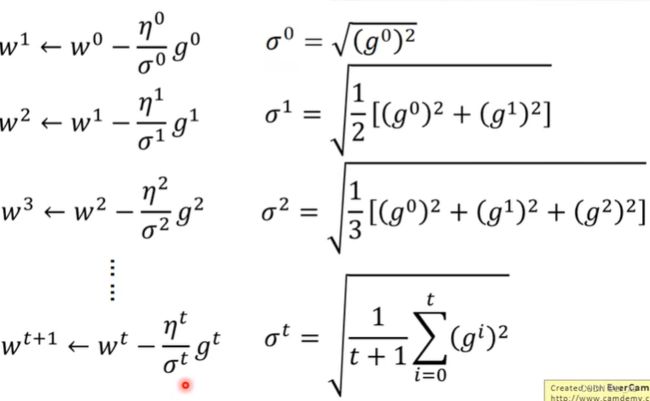NLP-机器学习-监督学习-回归

一个好的总结：机器学习知识点全面总结_GoAI的博客-CSDN博客_机器学习笔记

监督学习和无监督学习很好区分：是否有监督（supervised），就看输入数据是否有标签（label），输入数据有标签，则为有监督学习，没标签则为无监督学习。 

1.监督学习又分为“回归”和“分类”问题

        回归：是针对于连续的数据进行数据拟合，得到一个函数用于预测。

        分类：是针对于离散的数据进行数据分类，预测数据分属于不同的类别。5

2.假设你经营着一家公司，你想开发学习算法来处理这两个问题：

1. 你有一大批同样的货物，想象一下，你有上千件一模一样的货物等待出售，这时你想预测接下来的三个月能卖多少件？
2. 你有许多客户，这时你想写一个软件来检验每一个用户的账户。对于每一个账户，你要判断它们是否曾经被盗过？

那这两个问题，它们属于分类问题、还是回归问题?

问题一是一个回归问题，因为你知道，如果我有数千件货物，我会把它看成一个实数，一个连续的值。因此卖出的物品数，也是一个连续的值。

问题二是一个分类问题，因为我会把预测的值，用 0 来表示账户未被盗，用 1 表示账户曾经被盗过。所以我们根据账号是否被盗过，把它们定为0 或 1，然后用算法推测一个账号是 0 还是 1，因为只有少数的离散值，所以我把它归为分类问题。

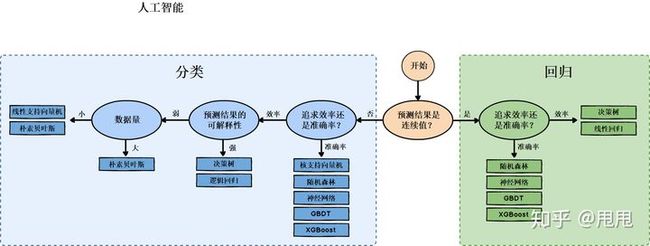
3.监督学习算法的选择

4.回归算法和相应实例：【机器学习】9种回归算法及实例总结，建议学习收藏_我爱Python数据挖掘的博客-CSDN博客_机器学习回归

4.回归问题之 是否净化宝可梦  李宏毅机器学习中文课程 - 网易云课堂

属于线性回归中：单变量线性回归和多变量线性回归：

        1求.宝可梦进化后战斗力 f（x)=ycp 这个函数f（xcp战斗力（xs，xhp，xh，.....) ) = ycp        

        2.假设f（x)= ycp=bi+wi *xcp;求具体b，w

        3.给出训练集[xi,yi]

        4.衡量w，b参数好坏，L(fi)=L(wi,bi)=误差= 这里用方差（方差越小，代表误差越小）

        5.找L（wi，bi）最小

        6.这里用到梯度概念 ：梯度（gradient），我去复习复习

7.假设只有一个 参数W情形

...........

8.结果：

 9.用测试集 test data去测试

 10. 多项式回归

考虑到上述model的误差较大，换一个model。对于多项式回归，一些自变量的幂大于 1。例如，我们可能会提出如下二次模型：

 

           训练集：   测试集：误差：

 当是2次：15.4       18.4

 当是3次：15.3       18.1

 当是4次：14.9       28.8

 当是5次：12.8       238.1

显然不是训练集误差越小，意味着model越好。  还要看测试集

11.过拟合

overfitting则通常是说训练习得的model对于测试集性能很差，而对训练集性能很好，也就是对训练集是overfitting，有很差的generalization（泛化能力），测试集的数据是我们的模型不曾见过的（参数无法基于此来训练）。训练集的不完备性是导致出现拟合问题的主要原因，而数据的不完备是不可避免的（如果我们的训练集是完备的，具有所有pattern下的数据，那么整个问题就不是learning problem，而是test problem，我们其实是验证而不是学习），因此出现拟合问题也是不可避免的。

12.

 误差来源  偏差（bias）和方差（variance）

与过拟合与欠拟合

偏差是你射击的平均值和中心点的差距，方差描述的是每一次射中的点和偏差的差距

复杂的模型造成了过拟合

因为训练数据过少导致高阶模型容易把数据噪声“当真”

model越复杂，需要的数据越多。

模型越简单，过拟合风险小，但是模型本身固有偏差大。模型越复杂，模型越无偏，但是方差大，过拟合风险大

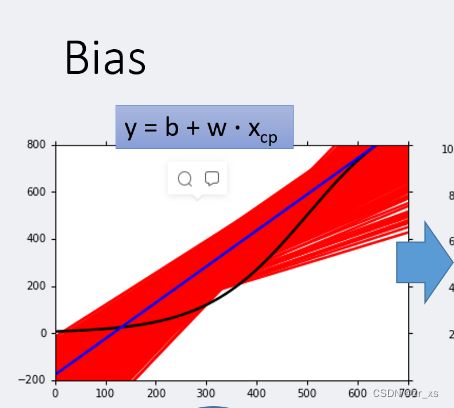
左边：一次                                                          右边：3次

 

回归中，复杂的模型包含简单的模型（令高次项系数为0）。

模型在拟合数据时，越简单的模型，受到特殊的取样数据点的影响越小，所以方差越小。

一般来说，

简单的模型（左侧）有大的bias和小的variance【喵的本来不准，但误差小-瞄错位置了】(欠拟合)
复杂的模型（右侧）有小的bias和大的variance【瞄得越来越准，但误差越来越大】（过拟合）

核心：找到一个平衡在考虑 bias和variance时候， 误差是最小的

解决方法：

（1）当在 训练集 误差小，测试集误差大：过拟合，variance大。

要增加测试集数据 。 或者   regularization平滑化，在现有Features不变情况下，降低部分不重要Features的影响力。笔记 | 什么是Regularization - 知乎，但是可能会影响到bias。

（2）当在 训练集 误差大                         ：欠拟合，bias大，瞄错位置了。
重写model，考虑更多因素。

测试集应尽可能符合部署真实场景的分布，否则交叉验证再高也是徒劳，最好的数据集应该设为测试集；也就是公开的测试集和私有的测试集（即验证集）的数据分布是有出入的，因此各自的偏差bias是不一样的，从而导致最终的测试误差更大

待学习：

训练集、验证集、测试集的划分

当训练有监督的机器学习模型时，通常我们需要将原数据集分割为两部分：训练集和测试集。

（1）从而使用训练集的数据来训练模型；

（2）模型在测试集上测试后，再用测试集上的误差近似模型在现实场景中的泛化误差。

（3）我们为什么还需要验证集？在机器学习中，我们不仅需要作模型与模型之间类的比较，对于某一类模型内部，也要不断进行筛选，涉及到模型自身的评估以及超参数的调整，我们就需要从训练集中再次划分出验证集。

可以get到几个点：

（1）验证集和测试集不同。

（2）验证集来自训练集的再划分。

（3）验证集的划分是为了模型选择和调参

（4）测试集是用来测试学习器对新样本的判别能力，用测试误差作为泛化误差的近似值。

交叉验证

(1) 将数据集分为训练集和测试集，测试集放在一边。
(2) 将训练集分为 k 份，每次使用 k 份中的1 份作为验证集，其他全部作为训练集。
(3) 通过 k 次训练后，得到了 k 个不同的模型。
(4) 评估 k 个模型的效果，从中挑选效果最好的超参数。
(5) 使用最优的超参数，然后将 k 份数据全部作为训练集重新训练模型，得到最终所需模型，最后再到测试集上测试。

==================================================================================================================================梯度下降

1.推荐：梯度下降算法原理讲解——机器学习_zhangpaopao0609的博客-CSDN博客_梯度下降

这里model 函数有2个参数，上标0代表初始值， 代表学习率。倒三角代表梯度向量

 2.如何调学习率 learnling rate

对于学习率：

在参数1维，2维度

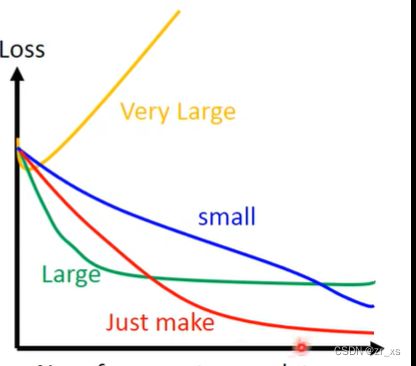
红色：刚刚好可以走到最低点，速度刚刚好

蓝色：学习率太小，速度太慢

绿色，黄色：学习率太大，走不到最低点

对于多维度：可以根据loss 观察学习率的大小

 

 tensorflow迭代可以选择显示loss和精确度甚至是你自定义的函数。c的话就要靠自己编程了。

梯度下降过程中，固定学习率并不合理。学习率太大，可能导致loss不减小反而增大；学习率太小，loss会减小得很慢。

如何自动的调整 learnling rate：

基本原则是随着参数迭代更新，学习率应该越来越小，比如（学习率），最开始学习率大，可能会快速的到达目标附近，到达附近后，减小学习率进行微调。

更好的方法：

方法1：

每个参数有各自的学习率，比如Adagrad：

对某一个参数 w，用Adagrad 学习率每次除以过去对该参数所有 微分值的 均方根

g0是一个数，不是一个向量，因为这里的w只代表一个参数，一个参数求出来的微分就是一个数，而之前讲的是多个参数求偏微分最后会得到一个梯度即向量。这里的Adagrad是对每一个 参数都有自己的学习率，g0是该参数对损失函数的偏微分，是一个数值。

结合上面 （学习率）：

 学习率 = 上一个学习率/根号下（所有微分的平方和）

作用：

起到的效果是在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。

在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度

​

缺点：

由于是累积平方梯度，导致学习率过快接近0

用adam就完美解决了，融合momentum和adagrad

​

方法2：

（SGD）使训练更快，，随机梯度下降，普通梯度下降中需要计算所有样本的Loss，而SGD只计算一个样本的Loss，然后进行梯度下降。

方法3：

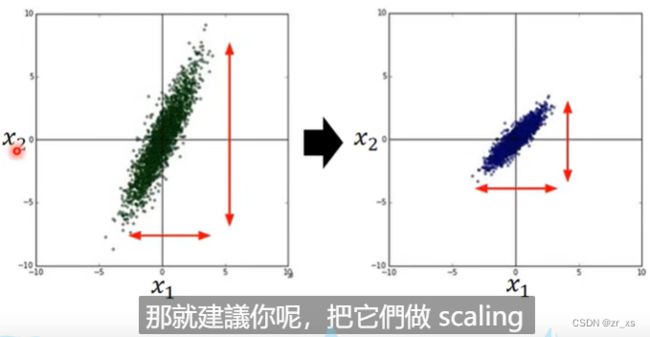
特征放缩（Feature Scaling）归一化参数

数据特征缩放（Feature Scaling）是一种将数据的不同变量或特征的方位进行标准化的方法。在数据处理中较为常用，也被称之为数据标准化（Data Normalization）

让 计算量变小，更好计算。这就是特征缩放，通过求对数或者指数等使数据分布范围近似。从优化上讲，就是目标函数条件数比较差，导致梯度下降很慢

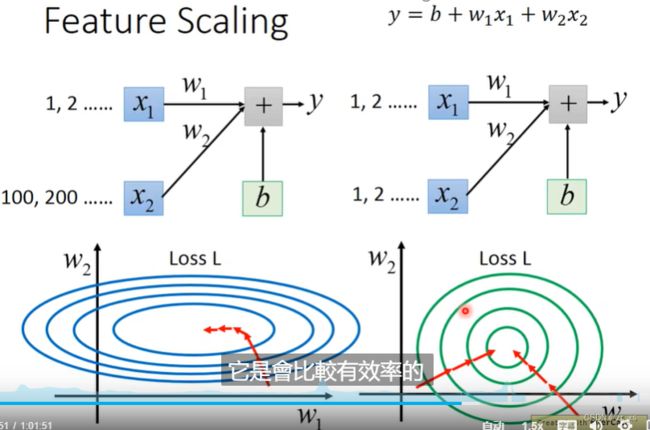
 对左图： w1*x1+w2*x2,因为输入x2大太。在loss中w2对损失函数影响也大。更新参数w的时候导致梯度下降很慢。

特征缩放的几种方法：特征缩放（Feature Scaling） - HuZihu - 博客园

        最大最小值归一化、均值归一化、标准化 / z值归一化。

 例如上图：对第i列(组)参数，求其平均和标准差，更新参数：x[i][j] = (x[i][j] - mean_x[j]) / std_x[j] #(x=x-mean_x)/std_x;

在实际应用中，通过梯度下降法求解的模型一般都是需要归一化的，比如线性回归、logistic回归、KNN、SVM、神经网络等模型。 但树形模型不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率，如决策树、随机森林(Random Forest)。 归一化和标准化主要是为了使计算更方便 比如两个变量的量纲不同 可能一个的数值远大于另一个那么他们同时作为变量的时候 可能会造成数值计算的问题，比如说求矩阵的逆可能很不精确 或者梯度下降法的收敛比较困难。​

机器学习 · 监督学习篇 I 监督学习是什么 - 知乎

这里推荐一个:李宏毅2020机器学习课程笔记（一）_iteapoy的博客-CSDN博客