2023.04.30 学习周报

---

摘要

This week, I read a computer science about time series prediction. This paper proposes a new traffic speed prediction model, LC-RNN, which realizes more accurate traffic speed prediction than existing solutions. In addition, due to the influence of local road constraints, a network embedded convolution structure is proposed to capture topological sensing features. Fusing it with other information, such as periodic and contextual factors, can further improve accuracy. Through a large number of experiments on two datasets, LC-RNN is proved to be superior to seven existing popular methods. In addition, I learn about ISOMAP algorithm, data preprocessing and metric tensor. For ISOMAP algorithm, I understand the basic idea of algorithm and implement it with code; simultaneously, I use the code to realize data cleaning, feature extraction and feature selection; Finally, expansion introduces an understanding of the metric tensor, namely coordinate transformation.

本周，我阅读了一篇与时间序列预测相关的文章。文章提出了一种新的交通速度预测模型LC-RNN，它实现了比现有解决方案更精确的交通速度预测。此外，由于受到局部道路限制的影响，提出了一种网络嵌入卷积结构来捕获拓扑感知特征。将其与周期性和上下文因素等其他信息融合，可以进一步提高准确性。通过在两个数据集上的大量实验，证明了 LC-RNN 优于七个现有的热门方法。 此外，我学习了ISOMAP降维算法、数据预处理和度规张量的相关内容。对于ISOMAP算法，我理解了算法的基本思想并用代码去实现它；同时，我用代码实现了数据清洗、特征提取和特征选择；最后，展开介绍度规张量的一个理解，即坐标变换。

---

文献阅读

1.题目

文献链接：LC-RNN A Deep Learning Model for Traffic Speed Prediction

2.摘要

Traffic speed prediction is known as an important but challenging problem. In this paper, we propose a novel model, called LC-RNN, to achieve more accurate traffic speed prediction than existing solutions. It takes advantage of both RNN and CNN models by a rational integration of them, so as to learn more meaningful time-series patterns that can adapt to the traffic dynamics of surrounding areas. Furthermore, since traffic evolution is restricted by the underlying road network, a network embedded convolution structure is proposed to capture topology aware features. The fusion with other information, including periodicity and context factors, is also considered to further improve accuracy. Extensive experiments on two real datasets demonstrate that our proposed LC-RNN outperforms seven well-known existing methods.

3.介绍

简介：
1）交通速度预测是指在历史观测的基础上，对未来各路段的速度进行预测；
2）提出了一个更有效的模型 LC-RNN，以支持精确的路段粒度交通速度预测；
3）LC-RNN 无缝集成了 CNN 和 RNN，以学习可以参考周围区域动态的速度波动模式，并采用嵌入卷积的道路网络来解决底层道路网络的约束；
4）通过自适应地与包括周期性和上下文因素在内的其他信息融合，进一步提高了准确性。

分析：
1）问题：预测接下来几个时间间隔内，在某条道路上车辆行驶的平均速度。
2）关键点：提出了用 look - up 来构造由每条道路及其相连道路所形成的速度矩阵，接着用 CNN 来提取相邻“道路速度”的空间依赖关系，然后进一步采用 LSTM 从时间序列的角度来提取特征，最后融合天气和周期信息得到整个网络的输出。

4.本文贡献

1）LC-RNN 采用道路网络嵌入卷积的方法，来学习更多有意义的空间特征。基于一组拓扑感知查找操作，卷积层能够捕获受底层道路网络限制的复杂交通演变模式。
2）LC-RNN 以合理的方式将 RNN 和 CNN 无缝集成，充分发挥各自的优势。基本思路是将 CNN 提取的周边区域特征馈送到 RNN 中学习时间序列模式，从而通过参考周边区域动态实现更准确的速度预测。
3）LC-RNN 考虑了周期性和环境因素，通过可学习的参数矩阵自适应地将结果与这些信息融合，从而获得更准确的预测结果。
4）使用北京的出租车轨迹和上海的小型道路网络来评估 LC-RNN 模型，结果表明，与七个基准测试相比，LC-RNN 模型具有明显的优势。

5.数据处理

在实际情况中，道路的连接是丛横交错的，并且存在对于某两个地点来说是单向通行的。于是，采用有向图来描绘道路结构：

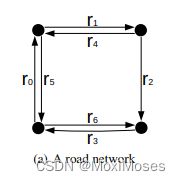
对于每条路上，在某个时间间隔 t 内的平均速度：

总的来说，要解决的问题就是给定历史数据 Xi，即历史速度向量，来预测 Xt+1, Xt+2, … 时刻的速度向量，即下一个或几个时刻每条道路可能的速度。

6.模型

网络模型的结构图如下所示：

1）LC-RNN 由多个查找卷积层、循环层、周期性提取层和上下文提取层组成，分别对局部空间演化、长时间依赖、周期性和上下文因素进行建模；
2）在输入中，蓝色块和红色块就是速度向量；
3）从上往下，第一层是卷积捕捉局部空间演化信息，下面那层是 LSTM 处理捕捉过来的空间信息；
4）Periodicity Learning 表示模拟周期信息，Context Learning 表示模拟天气、假期等信息。

6.1 look - up操作

"look-up"操作指如何构造每条道路对应的速度矩阵，即由多个相邻时刻的速度向量构成。

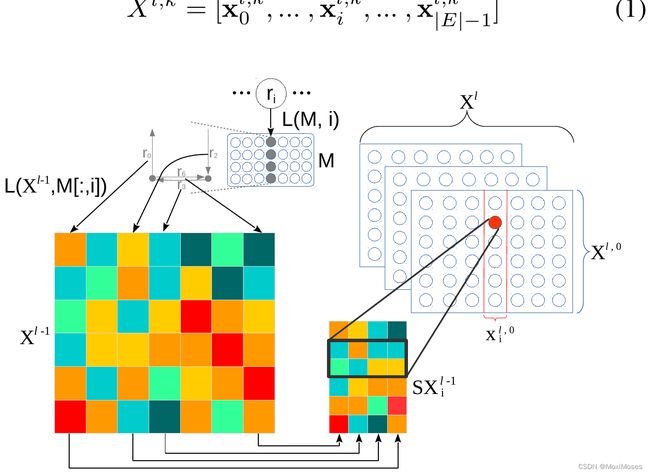
1）设计了一个查找卷积层，将道路网络拓扑嵌入到卷积中，以捕获更多有意义的空间特征；
2）用 t 时刻的前4个时间构成的速度矩阵根据 M 来索引得到每条道路相邻的所有道路的速度，并构成一个矩阵；
3）对得到的矩阵分别进行卷积操作，并且对用同一个卷积核作用得到每一列构成一个通道 X(l,k)。

6.2 LSTM

经过 look-up 操作后得到的输出 X^N 有三个维度，分别代表了时间间隔数，道路总数，卷积后的通道数。假设输出得到的 X 形状为 [4, 5, 2]，即一共有 4 个时刻，5 条道路，2 个通道。然后，这个输出进入 LSTM 需要通过 reshape 后才能作为输入，公式如下所示：

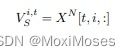
由此可知，当time_step=4，dim=2，batch_size=5时，只需要将 X 变为 [5, 4, 2] 即可，接着就是对 LSTM 的最后一个时刻的输出结果做非线性变换。

6.3 周期模拟及额外因素

1）对于这种时空数据，一般都会受到周期模拟和额外因素这两方面的影响；
2）文章中采用了两个全连接来分别模拟近几天和近几周的周期规律；
3）对于天气和节假日等额外因素，也采用了两个全连接来进行处理；
4）融合方式是基于权重的融合方式。

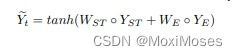
7.实验

7.1 数据集

文章使用来自北京和上海的两个数据集来测试 LC-RNN 模型：
1）北京：
采集时间为2016年3月1日至7月31日，主要提取了一个超过1万个主要路段的图，每天有超过200万个轨道覆盖着道路网络。前4个月的数据作为训练集，剩下1个月的数据作为测试集。
2）上海：
采集时间为2015年3月1日至4月31日，主要提取了一个大约1500条主要道路的小路网。最后15天的数据为测试集，其余的数据为训练集。

7.2 基线

1）SVR：SVR是一种功能强大的回归方法，具有更强的泛化能力。
2）H-ARIMA：H-ARIMA是一种结合ARIMA和HA来预测未来价值的方法。
3）SAE：SAE是一种深度学习模型，用于学习通用的流量特征并预测未来值。
4）LSTM：LSTM可以有效处理长时间依赖性，减少梯度消失，适合用于速度预测。
5）GC：GC使用图卷积、池化和全连接来预测未来的速度。
6）DCNN：DCNN使用卷积、池化和全连接的深度卷积神经网络进行速度预测。
7）ST-ResNet：ST-ResNet利用残差网络对三个时间属性进行建模来进行预测。

7.3 实验表现

1）在北京数据集上不同方法的比较：

根据实验结果，可以发现LC-3-RNN-E-BN将误差降低到5.274，显著提高了准确率。

2）在北京数据集上的预测性能：

当时间间隔变长时，预测性能会变得更好一些，这是由于随着时间间隔的增大，交通速度变得更加平稳。结果表明，该模型可以有效地预测路网上的交通速度。但随着数量的增加，性能会变得更差，这是因为被预测的时间间隔与当前时刻之间的交通速度相关性降低。

3）在上海数据集上不同方法的比较：

实验结果表明模型在不同规模的路网上具有良好的泛化性能，并且改变时间区间大小和预测区间数的结果也与北京的结果相似。

8.结论

1）提出了一种新的基于深度学习的 LC-RNN 模型来预测交通速度；
2）将 CNN 和 RNN 无缝集成，学习可以参考的周边区域动态的速度波动模式，并采用路网嵌入卷积来表示底层路网的约束条件；
3）通过自适应地融合其他信息，如周期性和上下文因素，进一步提高了预测的准确性；
4）在两个实际数据集上的实验结果证明了 LC-RNN 模型对 TSP 问题的有效性。

ISOMAP

1.基本思想

ISOMAP（等距特征映射）与前面学习的 MDS 降维算法是差不多的，差别在于ISOMAP 使用一个更合适的距离度量dij，使得该降维算法更适用于流形的数据。

2.欧氏距离

一般来说，考虑用欧氏距离作为距离的度量，但这一度量对非线性的流形数据并不是很适用。如下图所示，嵌入二维流形中的三维数据点分布：

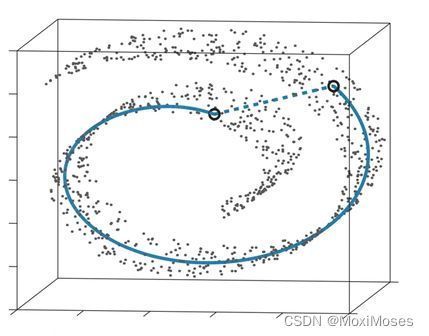
对于这张图而言，虽然数据是三维的，但从分布上来看，它是嵌入到了一个扭曲的二次曲面中。在数学上，这个二次曲面是一个流形。现在想要从数据中学习出这一流形，这种任务被称为流形学习。但是如果使用的是欧氏距离的话，就不能很好地反映两点间的真实远近关系。

3.折线近似曲线

因此，想要对任意两个数据点，都用一条曲线的长度来表示它们之间的距离。但曲线的长度是比较难计算的，即便知道曲线的解析方程，我们也要用到积分。因此我们考虑用一批折线来对其进行近似：

将二维曲面展开成一个二维平面，可以更加直观地看出折线与曲线的关系：

4.计算折线长度

当流形数据中的两个样本点有一定距离时，欧氏距离不能很好地反映它们之间的真实距离。但是当两个样本的欧氏距离足够小的时候，这两个样本的真实情况会比较接近。此时，可以使用欧氏距离去反映两个样本的距离情况。

考虑对每个样本选取它的 k 个最近的样本，将该样本与这 k 个邻居的欧氏距离计算出来，加入到原始的距离矩阵中。而该样本与其它点的初始距离设定为无穷大，此时会把原本对称的距离矩阵变得不对称，因此可以将其看做一张有向图的邻接矩阵，进而考虑用有向图的最短路径算法来迭代求解。

5.Floyd-Warshall算法

算法思想：若存在k，使得dij > dik + dkj，则dij = dik + dkj。即只要 i 到 j 有更短的路，那么就用走这条路，时间复杂度为O(n^3)。

Floyd算法的python实现：

import numpy as np


# D为欧氏距离阵，n_neighbors为k近邻中的k
def Floyd(D, n_neighbors=15):
    # 正无穷大
    Max = np.max(D) * 1000

    # n1是矩阵的维数
    n1, n2 = D.shape
    k = n_neighbors

    # 构造一个元素全是正无穷大的矩阵D1
    D1 = np.ones((n1, n1)) * Max

    # axis=1表示对行排序，然后返回排序后元素原来的索引
    D_arg = np.argsort(D, axis=1)

    # 循环填充k近邻的欧氏距离进入D1
    for i in range(n1):
        D1[i, D_arg[i, 0:k + 1]] = D[i, D_arg[i, 0:k + 1]]

        # 三层暴力循环求解最短路径
        for k in range(n1):
            for i in range(n1):
                for j in range(n1):
                    if D1[i, k] + D1[k, j] < D1[i, j]:
                        D1[i, j] = D1[i, k] + D1[k, j]
    return D1


# 生成7*7的随机矩阵作为距离阵
D = np.random.randint(1, 10, (7, 7))
print(D)

# 设对角线元素为0
for i in range(7):
    D[i, i] = 0

# 将上三角部分复制到下三角部分
D = np.triu(D)
D += D.T - np.diag(D.diagonal())

print(D)
# 调用floyd函数
D1 = Floyd(D, n_neighbors=2)
print(D1)

输出结果：

[[7 4 3 5 3 6 5]
 [8 1 7 2 5 4 1]
 [7 2 2 2 6 6 7]
 [3 1 9 7 2 4 6]
 [3 5 9 5 1 3 1]
 [1 7 2 9 2 4 4]
 [8 7 5 6 2 9 2]]
 
[[0 4 3 5 3 6 5]
 [4 0 7 2 5 4 1]
 [3 7 0 2 6 6 7]
 [5 2 2 0 2 4 6]
 [3 5 6 2 0 3 1]
 [6 4 6 4 3 0 4]
 [5 1 7 6 1 4 0]]
 
[[0. 5. 3. 5. 3. 6. 4.]
 [4. 0. 4. 2. 2. 4. 1.]
 [3. 4. 0. 2. 4. 6. 5.]
 [5. 2. 2. 0. 2. 4. 3.]
 [3. 2. 4. 2. 0. 3. 1.]
 [6. 4. 6. 4. 3. 0. 4.]
 [4. 1. 5. 3. 1. 4. 0.]]

其中：np.argsort函数的作用是对一个向量[1,3,5,2,4]，它先将其进行排序后得到[1,2,3,4,5]，然后返回这些数在原向量中对应的索引[0,3,1,4,2]。

6.ISOMAP算法

1）根据给定的欧氏距离阵，利用最短路径算法得到调整后的距离阵；
2）将调整后的距离阵代入MDS算法框架中。

ISOMAP算法的python实现：

import numpy as np
from sklearn.datasets import make_s_curve
import matplotlib.pyplot as plt
from sklearn.manifold import Isomap
from mpl_toolkits.mplot3d import Axes3D


# 1.floyd算法
def floyd(D, n_neighbors=15):
    Max = np.max(D) * 1000
    n1, n2 = D.shape
    k = n_neighbors
    D1 = np.ones((n1, n1)) * Max
    D_arg = np.argsort(D, axis=1)
    for i in range(n1):
        D1[i, D_arg[i, 0:k + 1]] = D[i, D_arg[i, 0:k + 1]]
    for k in range(n1):
        for i in range(n1):
            for j in range(n1):
                if D1[i, k] + D1[k, j] < D1[i, j]:
                    D1[i, j] = D1[i, k] + D1[k, j]
    return D1


# 2.计算两点间的距离
def cal_pairwise_dist(x):
    sum_x = np.sum(np.square(x), 1)
    dist = np.add(np.add(-2 * np.dot(x, x.T), sum_x).T, sum_x)
    return dist


# 3.MDS算法
def my_mds(dist, n_dims):

    dist = dist ** 2
    n = dist.shape[0]
    T1 = np.ones((n, n)) * np.sum(dist) / n ** 2
    T2 = np.sum(dist, axis=1) / n
    T3 = np.sum(dist, axis=0) / n

    B = -(T1 - T2 - T3 + dist) / 2

    eig_val, eig_vector = np.linalg.eig(B)
    index_ = np.argsort(-eig_val)[:n_dims]
    picked_eig_val = eig_val[index_].real
    picked_eig_vector = eig_vector[:, index_]

    return picked_eig_vector * picked_eig_val ** 0.5


# 4.ISOMAP算法(使用更合适的距离度量，调用MDS算法实现)
def my_Isomap(data, n=2, n_neighbors=30):
    D = cal_pairwise_dist(data)
    D[D < 0] = 0
    D = D ** 0.5
    D_floyd = floyd(D, n_neighbors)
    data_n = my_mds(D_floyd, n_dims=n)
    return data_n


# 5.画图
def scatter_3d(X, y):
    fig = plt.figure(figsize=(6, 5))
    ax = fig.add_subplot(111, projection='3d')
    ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.hot)
    ax.view_init(10, -70)
    ax.set_xlabel("$x_1$", fontsize=18)
    ax.set_ylabel("$x_2$", fontsize=18)
    ax.set_zlabel("$x_3$", fontsize=18)
    plt.show()


if __name__ == '__main__':
    X, Y = make_s_curve(n_samples=500,
                        noise=0.1,
                        random_state=42)

    data_1 = my_Isomap(X, 2, 10)

    data_2 = Isomap(n_neighbors=10, n_components=2).fit_transform(X)

    plt.figure(figsize=(8, 4))
    plt.subplot(121)
    plt.title("my_Isomap")
    plt.scatter(data_1[:, 0], data_1[:, 1], c=Y)

    plt.subplot(122)
    plt.title("sklearn_Isomap")
    plt.scatter(data_2[:, 0], data_2[:, 1], c=Y)
    plt.savefig("Isomap1.png")
    plt.show()

与sklearn实现的效果进行对比：

7.总结

高维空间中的数据大多数都具有相同的特点，因此会嵌入到一个流形中，而不是随机分散在高维空间中。高维数据相同特征的数目就是流形的维度，也就是我们降维的目标空间维数，这个维度需要一定的人为主观判断。其中Isomap算法使用一个更合适的距离度量，能够保留数据点之间的非线性关系。

数学建模

1.数据预处理

数据预处理一般分为三步：
1）数据清洗：去除缺失数据或异常数据，确保数据的质量。
2）特征提取：提取与模型预测目标相关的特征，并对特征进行缩放和归一化处理。
3）特征选择：选择对模型预测结果影响最大的特征，并剔除不重要的特征。

python代码实现：

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

root = "../data2"
city = "河池市"
station = "市环保站"
excel = f"{root}/{city}/{station}.xlsx"

# 1.数据清洗
data = pd.read_excel(excel, index_col=0).drop(["城市", "站点名称"], axis=1)
# 删除缺失值
data.dropna(inplace=True)
print("--------第1步 数据清洗--------")
print(data)

# 2.特征提取
scaler = StandardScaler()
data = scaler.fit_transform(data)
print("--------第2步 特征提取--------")
print(data)

# 3.特征选择
pca = PCA(n_components=4)
data = pca.fit_transform(data)
print("--------第3步 特征选择--------")
print(data)

输出结果：

--------第1步 数据清洗--------
       SO2  PM2.5   PM10  NO2    O3   CO
0     49.0  107.0  162.0   50  48.0  2.4
1     23.0   87.0  137.0   54  78.0  1.1
2     87.0  131.0  160.0   62  60.0  2.8
3     27.0  133.0  123.0   53  35.0  1.4
4     14.0   90.0  109.0   39  16.0  1.3
...    ...    ...    ...  ...   ...  ...
2552   8.0   16.0   25.0   10  46.0  0.7
2553   6.0   23.0   28.0   15  44.0  0.6
2554   6.0   20.0   27.0   14  64.0  0.7
2555   7.0   23.0   35.0   16  61.0  0.7
2556   6.0   33.0   42.0   20  44.0  0.7

[2551 rows x 6 columns]
--------第2步 特征提取--------
[[ 3.12825117  3.64514849  3.58325382  3.45908494 -0.85751051  4.37635623]
 [ 1.02009849  2.71021311  2.79334019  3.91618103  0.07718938  0.59132854]
 [ 6.20939741  4.76707095  3.52006073  4.8303732  -0.48363056  5.54098014]
 ...
 [-0.35830904 -0.42182041 -0.68227977 -0.65477984 -0.3590039  -0.57329536]
 [-0.27722624 -0.28158011 -0.42950741 -0.4262318  -0.45247389 -0.57329536]
 [-0.35830904  0.18588758 -0.20833159  0.03086429 -0.98213717 -0.57329536]]
--------第3步 特征选择--------
[[ 7.89567068  2.30188317  0.27631445 -0.20156858]
 [ 5.20028853 -0.6475203  -1.28192882  0.3453239 ]
 [10.53266579  3.01947861  2.50209532 -0.22513272]
 ...
 [-1.24028878  0.1365169  -0.08941     0.24074614]
 [-0.91672032  0.15121242 -0.20543904  0.35219222]
 [-0.43006831  0.43288169 -0.7459986   0.58712856]]

2.数据归一化

python实现数据归一化：

import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA


root = "../data2"
city = "河池市"
station = "市环保站"
excel = f"{root}/{city}/{station}.xlsx"
data = pd.read_excel(excel, index_col=0).drop(["城市", "站点名称"], axis=1)

# 1.Min-Max Scaling
# 将数据缩放到某一范围内
scaler = MinMaxScaler()
data = scaler.fit_transform(data)
print("--------第1种 Min-Max Scaling--------")
print(data)

# 2.Z-Score Normalization
# 将数据标准化为均值为0，标准差为1的正态分布
scaler = StandardScaler()
data = scaler.fit_transform(data)
print("--------第2种 Z-Score Normalization--------")
print(data)

# 3.Decimal Scaling
# 将数据缩放到某一位数
data = data / 10**np.ceil(np.log10(np.abs(data).max()))
print("--------第3种 Decimal Scaling--------")
print(data)

输出结果：

--------第1种 Min-Max Scaling--------
[[0.26857143 0.42063492 0.31854839 0.65671642 0.10591133 0.51282051]
 [0.12       0.34126984 0.26814516 0.71641791 0.17980296 0.17948718]
 [0.48571429 0.51587302 0.31451613 0.8358209  0.13546798 0.61538462]
 ...
 [0.02285714 0.07539683 0.04637097 0.11940299 0.1453202  0.07692308]
 [0.02857143 0.08730159 0.0625     0.14925373 0.13793103 0.07692308]
 [0.02285714 0.12698413 0.0766129  0.20895522 0.09605911 0.07692308]]
--------第2种 Z-Score Normalization--------
[[ 3.13156729  3.64692207  3.58575117  3.4621439  -0.85667693  4.38039061]
 [ 1.0216526   2.71175282  2.79555408  3.91942928  0.07849172  0.59264376]
 [ 6.21528876  4.76912518  3.52253541  4.83400003 -0.48260947  5.54585117]
 ...
 [-0.35790701 -0.42106417 -0.68131313 -0.6534245  -0.35792031 -0.5728168 ]
 [-0.27675645 -0.28078878 -0.42845006 -0.42478181 -0.45143718 -0.5728168 ]
 [-0.35790701  0.18679585 -0.20719487  0.03250357 -0.98136608 -0.5728168 ]]

3.特征提取

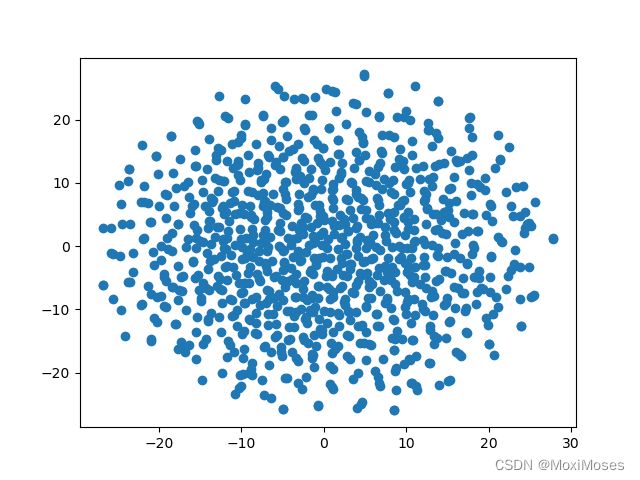
1）t-SNE：通过计算数据点之间的邻近关系，将高维数据转换为低维数据，即通过将高维数据嵌入到二维平面或三维空间中来可视化数据。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE

# 1.生成数据
np.random.seed(0)
data = np.random.randn(1000, 30)

# 2.使用t-SNE算法
tsne = TSNE(n_components=2)
tsne_data = tsne.fit_transform(data)

# 3.画图
plt.scatter(tsne_data[:, 0], tsne_data[:, 1])
plt.show()

输出结果：

2）PCA：通过对数据进行线性变换，使得数据变成最大方差的方向，即通过找到数据的主要方向并将数据投影到这些方向上来减少数据的维度。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA


# 1.生成数据
np.random.seed(0)
data = np.random.randn(1000, 30)

# 2.使用PCA算法
pca = PCA(n_components=2)
pca_data = pca.fit_transform(data)

# 3.画图
plt.scatter(pca_data[:, 0], pca_data[:, 1])
plt.show()

输出结果：

度规张量

1.点乘、内积

为了得到向量在基向量坐标轴上的分量，需要引入点乘和对偶坐标系。两个向量的点乘 u dot v = |u| cos(u, v) |v|，其几何含义为将向量v投影到u上面，再与u的长度相乘，得到的是一个矩形的面积。

定义两个向量，u的长度=4，v的长度=3。分别讨论在u, v夹角是锐角、直角、钝角、 180度的情况下，用图形来表明点乘的定义。
1）u, v夹角是锐角，u dot v = 8.65

2）u, v夹角是直角，u dot v = 0，即在垂直的情况下，不论u, v长度是多少，点乘结果都是0。

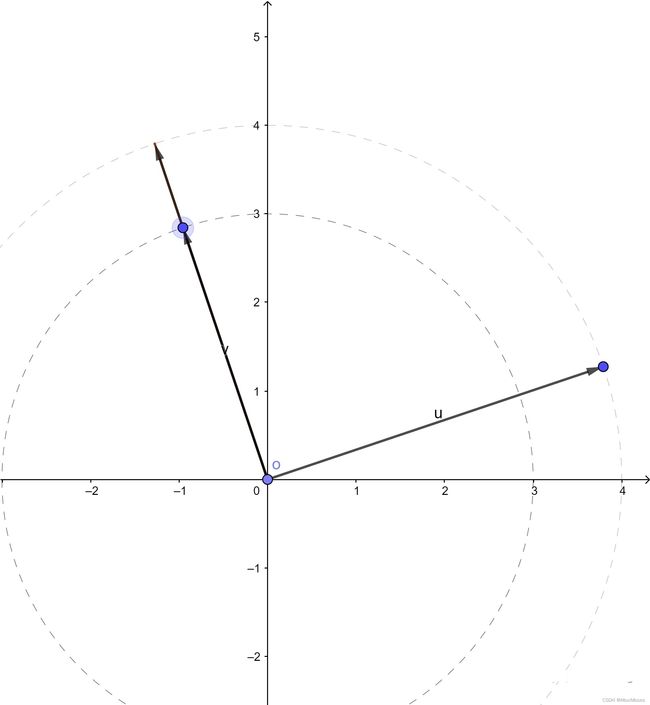
3）u, v夹角是180度，u dot v = -12

2.对偶坐标系

如果知道了一个坐标系g1, g2，那么通过下面方式定义其对偶坐标系g^1, g^2：
1）g1 dot g^1 = 1
2）g2 dot g^2 = 1
3）g1 dot g^2 = 0
4）g2 dot g^1 = 0
几何意义： g1 对偶基矢量垂直于除 g1 之外的矢量，而且它的长度与 g1 的长度有约束关系，即它的长度是 g1 长度的倒数。对偶基矢量的定义可以写成：

P dot gi = pi的证明：

计算一个向量在基向量 g1 上的分量：

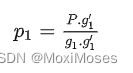
这个算式的几何含义：

从图中可以看出，P dot g1’ 是大矩形，而g1 dot g1’是小矩形。不难看出，大矩形面积是小矩形面积的多少倍，就是 P 在 g1’ 上的投影长度是 g1 在 g1’ 上的投影长度的多少倍。

需要注意的是，P在 g1’ 上的投影的绝对长度与 g1, g1’ 的长度无关。可以用三角函数来表达 P 在 g1’ 上的投影：

3.度量张量的一个理解：坐标变换

度量张量是将一个矢量在任意坐标系中的读数，转换到对偶坐标系上的读数的变换矩阵。其实这个过程可以和直角坐标系无关，因为我们有时也无法知道一个向量 P 以及这个坐标系的基向量 g1, g2 在直角坐标系上的读数。

假设基向量 g1 在对偶坐标系的读数是 g1 = a dot g^1 + b dot g^2，g2 在对偶坐标系的读数是 g2 = c dot g^1 + d dot g^2，则一个向量在坐标系 g1, g2 的读数到 g^1, g^2 的读数的转换关系为（不是直角坐标系的读数）：

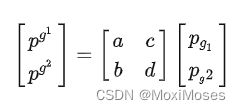
其中：a, b是基矢量 g1 在其对偶坐标系中相对 g^1, g^2 的分量；c, d是基矢量 g2 在其对偶坐标系中相对 g^1, g^2 的分量；而它们组成的矩阵就是度量张量。

---

总结

本周，我学习了Isomap降维算法，学完之后不难发现， Isomap算法是在MDS算法的基础上，使用一个更合适的距离度量，这是因为用欧氏距离作为距离的度量，这并不适用于非线性的流形数据，这也是Isomap算法更适用于流形数据的原因。在代码实现上，我们可以发现有对距离开平方和平方的操作，这是因为MDS算法为了计算方便，用距离的平方作为优化目标，而Floyd算法只会用到距离，而非距离的平方。此外，我学习数据预处理操作，步骤主要分为数据清洗、数据归一化和特征提取；以及继续学习了度规张量的相关内容，了解到度量张量可以被理解为坐标变化。下周，我将继续学习度规张量，去了解度规张量的本质。