深度学习笔记——神经网络(ANN)搭建过程+python代码
目录
1.多维数组的运算
(1)多维数组
(2)矩阵乘法
(3)神经网络的内积
2.3层神经网络的实现
(1)第一层加权和
(2)输入层到第1层的信号传递
(3)第1层到第2层的信号传递
(4)完整代码
1.多维数组的运算
(1)多维数组
多维数组的维数可以通过np.ndim()函数获得。此外,数组的形状可以通过实例变量shape获得。
二维数组也称为矩阵,数组的横向排列称为行(row),纵向排列称为列(column)
代码:
import numpy as np
A=np.array([1,2,3,4])
print("一维数组A的维数、形状、第一维度形状:")
print(A)
print(np.ndim(A))
print(A.shape)
print(A.shape[0])
B=np.array([[1,2],[3,4],[5,6]])
print("二维数组B的维数、形状、第一维度形状:")
print(B)
print(np.ndim(B))
print(B.shape)
print(B.shape[0])运行结果:
(2)矩阵乘法
矩阵乘积的计算方法如下图所示
矩阵的乘积可以通过NumPy的np.dot()函数计算(乘积也称为点积)
代码:
(2*2矩阵点积计算)
A = np.array([[1,2],[3,4]])
print(A.shape)
B = np.array([[5,6],[7,8]])
print(B.shape)
print(np.dot(A,B))运行结果:
(2*3矩阵和3*2矩阵点积运算)
A = np.array([[1,2,3],[4,5,6]])
print(A.shape)
B = np.array([[1,2],[3,4],[5,6]])
print(B.shape)
print(np.dot(A,B))运行结果:
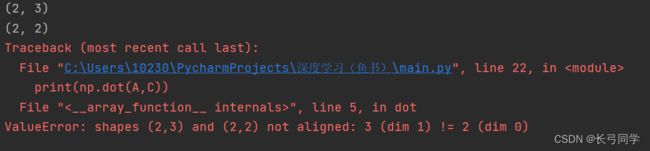
(2*3和2*2矩阵进行点积运算)
A = np.array([[1,2,3],[4,5,6]])
print(A.shape)
B = np.array([[1,2],[3,4],[5,6]])
C = np.array([[1,2],[3,4]])
print(C.shape)
print(np.dot(A,C))运行结果:
出现报错“ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)”,这是因为在多维数组运算中,两个进行点积运算的矩阵中的对应维度个数必须相同。
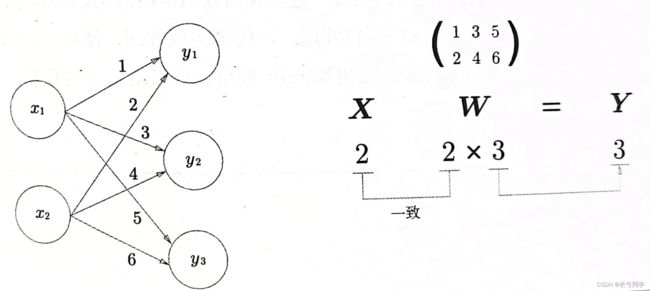
(3)神经网络的内积
使用numpy矩阵实现一个简单神经网络(省略了偏置和激活函数,只有权重)
下图为该简单神经网络的结构
代码:
X = np.array([1,2])
print(X.shape)
W = np.array([[1,3,5],[2,4,6]])
print(W)
print(W.shape)
Y = np.dot(X,W)
print(Y)
运行结果:
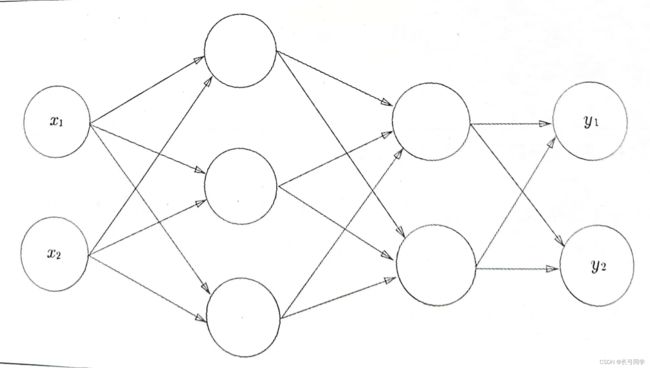
2.3层神经网络的实现
3层神经网络结构如下:
其中,该神经网络:输入层(第0层)有2个神经元,第1个隐藏层(第1层)有3个神经元,第2个隐藏层(第2层)有2个神经元,输出层(第3层)有2个神经元
增加表示偏置的神经元“1”,如下图所示:
(1)第一层加权和
使用矩阵的乘法运算,可以将第一层的加权和表示成下面的式子:
![]()
代码实现(这里将输入信号、权重、偏置设置为任意值)
X = np.array([1.0,0.5])
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])
A1 = np.dot(X,W1) + B1使用激活函数sigmoid后:
def sigmoid(x):
return 1 / (1 + np.exp(-x))
X = np.array([1.0,0.5])
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])
A1 = np.dot(X,W1) + B1
Z1 = sigmoid(A1)(2)输入层到第1层的信号传递
代码:
W2 = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
B2 = np.array([0.1,0.2])
A2 = np.dot(Z1,W2) + B2
Z2 = sigmoid(A2)
(3)第1层到第2层的信号传递
在这里我们定义了identity_function()函数(恒等函数),并将其作为输出层的激活函数。
(说明:输出层所用的激活函数,要根据求解问题的性质决定。一般地,回归问题可以使用恒等函数,二分类问题使用sigmoid函数,多元分类问题可以使用softmax函数)
def identity_function(x):
return x
W3 = np.array([[0.1,0.3],[0.2,0.4]])
B3 = np.array([0.1,0.2])
A3 = np.dot(Z2,W3) + B3
Y = identity_function(A3) (4)完整代码
def init_network():
network = {}
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1'] = np.array([0.1,0.2,0.3])
network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['b2'] = np.array([0.1,0.2])
network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
network['b3'] = np.array([0.1,0.2])
return network
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def identity_function(x):
return x
import numpy as np
def forward(network, x):
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'],network['b2'],network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
if __name__ == '__main__':
network = init_network()
x = np.array([1.0,0.5])
y = forward(network,x)
print(y)