蓝桥杯-15年，16年国赛 Python题解

目录

15年

方格填数

四阶幻方

穿越雷区

切开字符串

16年

随意组合

路径之谜

---

15年

方格填数

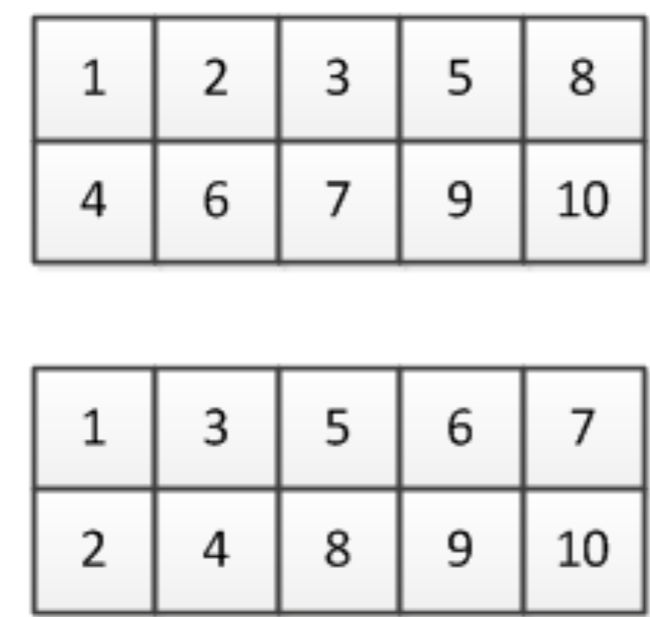
在2行5列的格子中填入1到10的数字。

要求：

相邻的格子中的数，右边的大于左边的，下边的大于上边的。

如图所示的2种，就是合格的填法。

请你计算一共有多少种可能的方案。

请提交该整数，不要填写任何多余的内容（例如：说明性文字）。

# 方案数
ans = 0
# 方格，多申请防止填充时越界
grid = [[0] * 10 for i in range(3)]
# 访问状态标记
# 下标从1开始
visit = [False for i in range(12)]


# 判断grid[x][y]位置的数字是否满足规则
def judge(x, y):
    # 只有一行的时候
    if x == 0:
        # 有多列和只有一列的时候
        if grid[x][y] > grid[x][y - 1] or y == 0:
            return True

    # 有两行的时候
    # 有多列和只有一列的时候
    if (grid[x][y] > grid[x][y - 1] and grid[x][y] > grid[x - 1][y]) or (y == 0 and grid[x][y] > grid[x - 1][y]):
        return True

    return False


# 深度搜索进行方格填充
def dfs(x, y):
    global ans
    # 搜索边界,已经填充完方格
    if x == 2:
        ans += 1
        return

    # 搜索过程
    for i in range(1, 11):
        # 如果当前数字没有被访问
        if not visit[i]:
            grid[x][y] = i
            #剪枝
            if juage(x, y):
                #状态标记
                visit[i] = True
                #填完一行了
                if y == 4:
                    dfs(x + 1, 0)
                else:
                    dfs(x, y + 1)
                #清除状态标记
                visit[i] = False


dfs(0, 0)
print(ans)

四阶幻方

把1~16的数字填入4x4的方格中，使得行、列以及两个对角线的和都相等，满足这样的特征时称为：四阶幻方。

四阶幻方可能有很多方案。如果固定左上角为1，请计算一共有多少种方案。

比如：

1 2 15 16

12 14 3 5

13 7 10 4

8 11 6 9

以及：

1 12 13 8

2 14 7 11

15 3 10 6

16 5 4 9

就可以算为两种不同的方案。

请提交左上角固定为1时的所有方案数字，不要填写任何多余内容或说明文字。

# 幻方每行，列，对角线的和
sum_value = 34
# 种类数
ans = 0
# 幻方,多申请防止越界
matrix = [[0] * 5 for i in range(5)]
# 每个数字的访问状态标记
visited = [0 for j in range(17)]


# 按照规则进行判断
def judge():
    now_sum = 0

    # 检查主对角线是否满足规则
    now_sum = sum(matrix[i][i] for i in range(4))
    if now_sum != sum_value:
        return False

    # 检测副对角线
    now_sum = sum(matrix[i][3 - i] for i in range(4))
    if now_sum != sum_value:
        return False

    # 检查每一行
    for i in range(4):
        if sum(matrix[i]) != sum_value:
            return False

    # 检查每一列
    for j in zip(*matrix):
        if sum(j) != sum_value:
            return False

    # 其余情况一律返回True
    return True


# 深度搜索进行幻方填充
def dfs(n):
    """

    :param n: 当前幻方已经填充的数字数量
    :return:
    """
    # 边界,16个数字都已填充完毕
    if n == 16:
        if judge():
            ans += 1
        return

    # 剪枝
    # 每完整的填完一行进行一下判断
    # 如果不满足规则不继续进行数字填充
    if n % 4 == 0:
        # 注意下标少1
        if sum(matrix[n // 4 - 1]) != sum_value:
            return

    # 深度搜索
    for i in range(2, 17):
        # 如果当前所要填充的数字没有被使用
        if visited[i] == 0:
            visited[i] = 1
            matrix[n // 4][n % 4] = i
            dfs(n + 1)

            # 回退
            visited[i] = 0


# 第一个数字填1
matrix[0][0] = 1
# 深度搜索
dfs(1)
print(ans)

穿越雷区

X星的坦克战车很奇怪，它必须交替地穿越正能量辐射区和负能量辐射区才能保持正常运转，否则将报废。

某坦克需要从A区到B区去（A，B区本身是安全区，没有正能量或负能量特征），怎样走才能路径最短？

已知的地图是一个方阵，上面用字母标出了A，B区，其它区都标了正号或负号分别表示正负能量辐射区。

例如：

A + - + -

- + - - +

- + + + -

+ - + - +

B + - + -

坦克车只能水平或垂直方向上移动到相邻的区。

数据格式要求：

输入第一行是一个整数n，表示方阵的大小， 4<=n<100

接下来是n行，每行有n个数据，可能是A，B，+，-中的某一个，中间用空格分开。

A，B都只出现一次。

要求输出一个整数，表示坦克从A区到B区的最少移动步数。

如果没有方案，则输出-1

例如：

用户输入：

5

A + - + -

- + - - +

- + + + -

+ - + - +

B + - + -

则程序应该输出：

10

import sys

# 方阵大小
n = int(input())
# 起点，终点坐标
Ax, Ay = 0, 0
Bx, By = 0, 0
# 移动方向上，右，下，左
direction = [[-1, 0], [0, 1], [1, 0], [0, -1]]
# 最小步数，初始为一个最大值
step = sys.maxsize
# 存储地雷地图,多申请
map_list = [[''] * (100 + 5) for i in range((100 + 5) + 1)]
# 地图上每个点的访问状态
map_visit = [[False] * (100 + 5) for j in range((100 + 5) + 1)]


# 判断
def judge(x, y, new_x, new_y):
    # 如果越界了
    if new_x < 1 or new_x > n or new_y < 1 or new_y > n:
        return False
    # 如果新移动的点与上一个点的取值相同
    if map_list[x][y] == map_list[new_x][new_y]:
        return False
    # 其余情况
    return True


# 深度搜索
def dfs(x, y, cnt):
    """

    :param x: 当前所在点的x坐标
    :param y: 当前所在点的y坐标
    :param cnt: 当前所走的步数
    :return:
    """
    global step
    # 边界
    # 到达终点
    if map_list[x][y] == 'B':
        # 更新最小步数
        step = min(step, cnt)
        return

    # 向上，右，下，左四个方向进行试探
    for i in range(4):
        new_x = x + direction[i][0]
        new_y = y + direction[i][1]
        # 深度搜索
        if not map_visit[new_x][new_y]:
            if judge(x, y, new_x, new_y):
                map_visit[new_x][new_y] = True
                dfs(new_x, new_y, cnt + 1)

                # 回退
                map_visit[new_x][new_y] = False


# 读入地图
for i in range(1, n + 1):
    temp_s = input().split()
    for j in range(1, len(temp_s) + 1):
        map_list[i][j] = temp_s[j - 1]
        # 起点
        if temp_s[j - 1] == 'A':
            Ax = i
            Ay = j
            map_visit[Ax][Ay] = 1

dfs(Ax, Ay, 0)
if step != sys.maxsize:
    print(step)
else:
    print(-1)

切开字符串

Pear有一个字符串，不过他希望把它切成两段。

这是一个长度为N（<=10^5）的字符串。

Pear希望选择一个位置，把字符串不重复不遗漏地切成两段，长度分别是t和N-t（这两段都必须非空）。

Pear用如下方式评估切割的方案：

定义“正回文子串”为：长度为奇数的回文子串。

设切成的两段字符串中，前一段中有A个不相同的正回文子串，后一段中有B个不相同的非正回文子串，则该方案的得分为A*B。

注意，后一段中的B表示的是：“...非正回文...”，而不是: “...正回文...”。

那么所有的切割方案中，A*B的最大值是多少呢？

【输入数据】

输入第一行一个正整数N（<=10^5）

接下来一行一个字符串，长度为N。该字符串仅包含小写英文字母。

【输出数据】

一行一个正整数，表示所求的A*B的最大值。

【样例输入】

10

bbaaabcaba

【样例输出】

38

【数据范围】

对于20%的数据，N<=100

对于40%的数据，N<=1000

对于100%的数据，N<=10^5

# 判断一个字符串string是否是回文序列
def is_cycle(string):
    # 字符串长度
    string_length = len(string)
    if string_length == 0:
        return False
    # 注意Python的除法
    n = string_length // 2
    # 判断是否是回文
    # 即判断以n为对称点的另一个位置上的字符
    # 是否和当前的相同
    # 不同即不是回文
    for i in range(n):
        if string[i] != string[string_length - i - 1]:
            return False
    # 其余情况就是回文字符串
    return True


# 寻找字符串string的所有子串的个数
def find_sub_string(string):
    # 用集合保证找到的子串的唯一性
    sub_string_set = set()
    # 子串的长度
    # 注意，字符串string自身也算作一个子串
    for sub_string_length in range(1, len(string) + 1):
        # 子串的起始位置
        for sub_string_index in range(0, len(string) - sub_string_length + 1):
            sub_string_set.add(string[sub_string_index:sub_string_index + sub_string_length])
    return len(sub_string_set)


# 寻找正回文子串
def find_positive_sub_string(string):
    # 保证唯一性
    positive_sub_string_set = set()
    # 正子串的长度
    # 注意，是奇数
    for positive_sub_string_length in range(1, len(string) + 1, 2):
        # 正子串起始位置
        for start in range(len(string) - positive_sub_string_length + 1):
            temp_string = string[start:start + positive_sub_string_length]
            if is_cycle(temp_string):
                positive_sub_string_set.add(temp_string)
    return len(positive_sub_string_set)


# 字符串长度
n = int(input())
# 字符串
string = input()
# 切割方案数
ans = 0
for i in range(1, n - 1):
    # 正回文子串数量
    A = find_positive_sub_string(string[:i])
    # 非正回文子串数量
    B = find_sub_string(string[i:]) - find_positive_sub_string(string[i:])
    ans = max(ans, A * B)

print(ans)

16年

随意组合

小明被绑架到X星球的巫师W那里。

其时，W正在玩弄两组数据 (2 3 5 8) 和 (1 4 6 7)

他命令小明从一组数据中分别取数与另一组中的数配对，共配成4对（组中的每个数必被用到）。

小明的配法是：{(8,7),(5,6),(3,4),(2,1)}

巫师凝视片刻，突然说这个配法太棒了！

因为：

每个配对中的数字组成两位数，求平方和，无论正倒，居然相等：

87^2 + 56^2 + 34^2 + 21^2 = 12302

78^2 + 65^2 + 43^2 + 12^2 = 12302

小明想了想说：“这有什么奇怪呢，我们地球人都知道，随便配配也可以啊！”

{(8,6),(5,4),(3,1),(2,7)}

86^2 + 54^2 + 31^2 + 27^2 = 12002

68^2 + 45^2 + 13^2 + 72^2 = 12002

巫师顿时凌乱了。。。。。

请你计算一下，包括上边给出的两种配法，巫师的两组数据一共有多少种配对方案具有该特征。

配对方案计数时，不考虑配对的出现次序。

就是说：

{(8,7),(5,6),(3,4),(2,1)}

与

{(5,6),(8,7),(3,4),(2,1)}

是同一种方案。

注意：需要提交的是一个整数，不要填写任何多余内容（比如，解释说明文字等）

import itertools
# 序列1
sequence_1 = [2, 3, 5, 8]
# 序列2
sequence_2 = [1, 4, 6, 7]
ans = 0


for item in itertools.permutations(sequence_2):
    r1 = (sequence_1[0] * 10 + item[0]) ** 2 + (sequence_1[1] * 10 + item[1]) ** 2 + (
                sequence_1[2] * 10 + item[2]) ** 2 + (sequence_1[3] * 10 + item[3]) ** 2
    r2 = (sequence_1[0] + item[0] * 10) ** 2 + (sequence_1[1] + item[1] * 10) ** 2 + (
                sequence_1[2] + item[2] * 10) ** 2 + (sequence_1[3] + item[3] * 10) ** 2
    if r1 == r2:
        ans += 1
print(ans)

路径之谜

小明冒充X星球的骑士，进入了一个奇怪的城堡。

城堡里边什么都没有，只有方形石头铺成的地面。

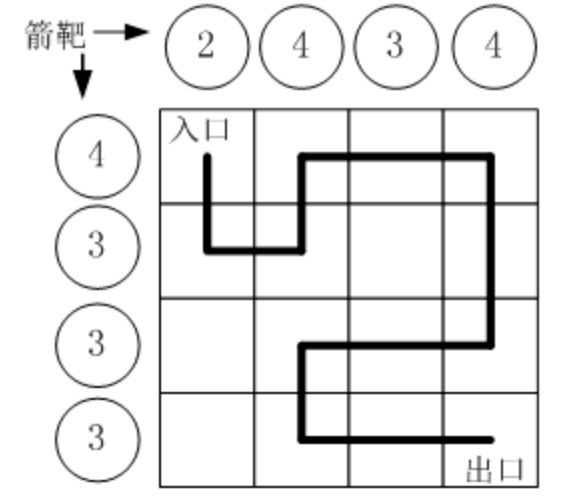
假设城堡地面是 n x n 个方格。如图所示。

按习俗，骑士要从西北角走到东南角。

可以横向或纵向移动，但不能斜着走，也不能跳跃。

每走到一个新方格，就要向正北方和正西方各射一箭。

（城堡的西墙和北墙内各有 n 个靶子）

同一个方格只允许经过一次。但不必走完所有的方格。

如果只给出靶子上箭的数目，你能推断出骑士的行走路线吗？

有时是可以的，比如图中的例子。

本题的要求就是已知箭靶数字，求骑士的行走路径（测试数据保证路径唯一）

输入：

第一行一个整数N(0

第二行N个整数，空格分开，表示北边的箭靶上的数字（自西向东）

第三行N个整数，空格分开，表示西边的箭靶上的数字（自北向南）

输出：

一行若干个整数，表示骑士路径。

为了方便表示，我们约定每个小格子用一个数字代表，从西北角开始编号: 0,1,2,3....

比如，图中的方块编号为：

0 1 2 3

4 5 6 7

8 9 10 11

12 13 14 15

示例：

用户输入：

4

2 4 3 4

4 3 3 3

程序应该输出：

0 4 5 1 2 3 7 11 10 9 13 14 15

# 北方箭数
north_number = [0 for i in range(25)]
# 西方箭数
west_number = [0 for i in range(25)]
# 地图上每个点的访问状态
visit = [[False] * 25 for i in range(26)]
# 箭靶上的箭是否已经拔完
flag = 0
# 路径坐标
ans = []
# 方向上，右，下，左
direction = [(-1, 0), (0, 1), (1, 0), (0, -1)]
# 地图
n = int(input())


# 深度搜索
def dfs(i, j):
    """

    :param i: 当前点横坐标
    :param j: 当前点纵坐标
    :return:
    """
    global n
    global flag
    # 如果当前点已经访问过
    # 或者北，西方向的箭靶上的箭已经被拔完
    # 或者已经到达终点
    if visit[i][j] or north_number[i] == 0 or west_number[j] == 0 or flag == 1:
        return
    visit[i][j] = True
    # 拔箭
    north_number[i] -= 1
    west_number[j] -= 1
    # 向四个方向试探
    if i != n - 1 or j != n - 1:
        if i < n - 1:
            dfs(i + 1, j)
        if i > 0:
            dfs(i - 1, j)
        if j < n - 1:
            dfs(i, j + 1)
        if j > 0:
            dfs(i, j - 1)
    else:
        k = 0
        for k in range(n):
            if north_number[k] != 0 or west_number[k] != 0:
                break
        if k == n:
            flag = 1
    if flag == 1:
        ans.append(i + n * j)
    # 回溯
    north_number[i] += 1
    west_number[j] += 1
    visit[i][j] = 0


s = input().split()
for i in range(len(s)):
    north_number[i] = int(s[i])
s = input().split()
for j in range(len(s)):
    west_number[j] = int(s[j])
dfs(0, 0)
print(ans)