八种排序算法(c++模板实现)------详细注释版
八种排序算法(c++模板实现)------详细注释版
前言
排序算法基本上学过数据结构都是有所学习的,本篇博客不再详细介绍每种算法的基础思想,会直接通过代码及注释的方式展示出算法,方便自己及已经入门同学日常回顾!
概述
| 排序 | 种类 |
|---|---|
| 内部排序 | 使用内存 |
| 外部排序 | 内存不够使用需要访问外存,常见算法有:多路归并排序、外分配排序等 |
内部排序算法种类
| 排序方式 | 排序种类 |
|---|---|
| 插入排序 | 直接插入排序、希尔排序 |
| 选择排序 | 简单选择排序、堆排序 |
| 交换排序 | 冒泡排序、快速排序 |
| 归并排序 | |
| 基数排序 |
算法基本概念
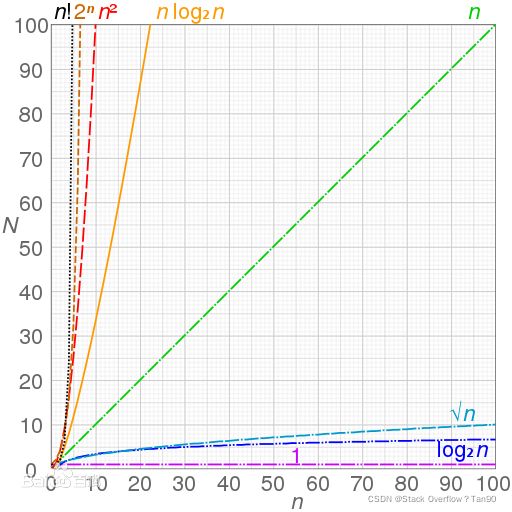
时间复杂度
空间复杂度
- 空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度,时间复杂度常用大O符号表述。
稳定性
- 两个及以上相同的元素在排序的过程中的相对位置不发生改变,那么就称之为稳定的排序!例如:待排序列(5, 2, 2)排序后变成(2, 2, 5),加粗的2和未加粗的2相对位置发生了改变,那么这就是不稳定的排序。
算法实现
直接插入排序
版本1
从头到尾将每一个元素,通过和其它元素比较放到相应的位置
template <typename T>
void insertSort(T arr[], int len)
{
int i, j;
for (i = 1; i < len; ++i)
{
if (arr[i] < arr[i - 1]) // 找到需要插入的元素
{
T tmp = arr[i]; // 保存需要插入的元素
j = i - 1;
while (tmp < arr[j] && j >= 0) // 将待排序的元素找到合适的位置
{
arr[j + 1] = arr[j]; // 依次将比tmp元素大的向后移动
--j;
}
arr[j + 1] = tmp;
}
}
}
版本2:折半插入排序
直接插入排序每次都是插入到一个已经排好的序列中,所以主要耗费时间就是查找待插入位置,所以可以使用二分法来查找插入位置,减少比对次数,提高效率。
template <typename T>
void insertSort2(T arr[], int len)
{
int i, j, low, high, mid;
for (i = 1; i < len; ++i)
{
T tmp = arr[i]; // 保存需要插入的元素
low = 0;
high = i - 1; // 设置查找范围
while (low <= high) // 折半查找
{
mid = (low + high) / 2; // 取中间值
if (tmp < arr[mid]) // 插入值比中间值小,那么查找左半表
{
high = mid - 1; // 定位到左子表
}
else
{
low = mid + 1; // 定位到右子表
}
}
// 找到插入位置,将大于插入值的元素后移
for (j = i - 1; j >= high + 1; --j)
{
arr[j + 1] = arr[j];
}
arr[high + 1] = tmp;
}
}
简单选择排序
版本1
在未排序的序列中找到当前的最大(小)值,并放到未排序序列的最后(前)面
template <typename T>
void selectSort(T arr[], int len)
{
int min;
T tmp;
// 每次选择当前未排序的最小的元素
for (int i = 0; i < len; ++i)
{
min = i;
// 在未排序的剩余元素中找到最小的元素
for (int j = i + 1; j < len; ++j)
{
// 如果找到比arr[min]还小的元素,更新最小元素位置
if (arr[min] > arr[j])
{
min = j;
}
}
// 当前待排序的第一个元素不是最小元素,则交换数据,
// 减少交换次数,提高效率
if (min != i)
{
tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
}
版本2 – 提升效率
同时记录当前待排序的最小值及最大值,这样就可以减少排序次数,提高效率
template <typename T>
void selectSort2(T arr[], int len)
{
int min, max;
T tmp;
// 同时记录当前待排序的最小值及最大值,这样就可以减少排序次数,提高效率
for (int i = 0; i < len / 2; ++i)
{
min = max = i;
// 双向减少比对次数
for (int j = i + 1; j < len - i; ++j)
{
// 分别记录当前一趟排序的最大值及最小值
if (arr[min] > arr[j])
{
min = j;
}
if (arr[max] < arr[j])
{
max = j;
}
}
// 如果最小值与最大值不是当前排序的最大值、最小值所在的位置,则交换数据
if (min != i)
{
tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
/* 如果最小值和最大值的位置正好相反,那么经过上面最小值的交换后,最大值
已经被交换到正确的位置,所以下面对最大值的交换则不需要了 */
if (min == len - 1 - i && max == i)
{
continue;
}
/* 如果当前待排序列的第一个元素是最大值,那么由于上面排序最小值时已经将最小值
覆盖到此处,并将之前的最大值换到min位置,所以需要更新最大值的位置 */
if (max == i)
{
max = min;
}
if (max != (len - i - 1))
{
tmp = arr[max];
arr[max] = arr[len - i - 1];
arr[len - i - 1] = tmp;
}
print(arr, len);
}
}
冒泡排序
版本1
依次比较未排序序列的相邻元素,依次将未排序序列的最大值放到末尾。类似于气泡上浮一样
template <typename T>
void bubbleSort1(T arr[], int len)
{
// 每一趟确定一个当前未排序的最大元素
for (int i = 0; i < len - 1; ++i)
{
// 设置flag标志位记录当前遍历有没有发生数据交换,
// 如果没有发生交换说明,数据已经排序好,不需要在排序了。
int flag = false;
for (int j = 0; j < len - i - 1; ++j)
{
// 如果前一个元素比后一个元素大,则交换,
// 这样就确定了当前未排序的最大元素
if (arr[j] > arr[j + 1])
{
T tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = true;
}
}
if (flag == false)
{
return;
}
}
}
版本2 – 提升效率
通过一趟排序分别正向冒泡、反向冒泡来确定一个最大值与最小值,减少排序次数,提高效率
template <typename T>
void bubbleSort2(T arr[], int len)
{
T tmp;
int high = len - 1;
int low = 0;
// 通过一趟排序分别正向冒泡、反向冒泡确定一个最大值与最小值,
// 减少排序次数,提高效率
while (high > low)
{
// 设置flag标志位记录当前遍历有没有发生数据交换,
// 如果没有发生交换说明,数据已经排序好,不需要在排序了。
int flag = false;
// 正向冒泡找到最大值
for (int i = low; i < high; ++i)
{
if (arr[i] > arr[i + 1])
{
tmp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = tmp;
flag = true;
}
}
--high; // 确定一个最大值后,减少排序的次数一次
// 反向冒泡,找到最小值
for (int j = high; j > low; --j)
{
if (arr[j] < arr[j - 1])
{
tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
flag = true;
}
}
++low; // 确定一个最小值后,减少排序次数一次
if (flag == false)
{
return;
}
}
}
快速排序
快排采用了分治的思想,排序的步骤如下:
- 分解:将数组
A[p...r]划分为两个(可能为空)的子数组A[p...q-1]和A[q+1...r],使得A[p...q-1]中的每一个元素都小于等于A[q], 而A[q]也小于等于A[q+1...r]的每一个元素。其中计算下标q也是划分的过程的一部分。 - 解决:通过递归调用快排,对数组
A[p...q-1]和A[q+1...r]进行排序
template <typename T>
int partition(T arr[], int low, int high)
{
T pivotKey = arr[low]; // 取数组第一个元素为枢轴
while (low < high) // 从数组两端向中间扫描
{
// 先从数组的右侧向左扫描
while ((low < high) && (pivotKey <= arr[high]))
--high; // 如果从右侧未找到比枢轴小的元素则左移
swap(arr[low], arr[high]); // 交换比枢轴小的值到左侧
// 从数组的左侧向右扫描
while ((low < high) && (arr[low] <= pivotKey))
++low; // 如果从右侧未找到比枢轴大的元素则右移
swap(arr[low], arr[high]); // 交换比枢轴大的值到右侧
}
arr[low] = pivotKey; // 将枢轴放在low == high的位置,这个位置也是枢轴的最终位置
return low; // 返回分界位置
}
template <typename T>
void quickSort(T arr[], int low, int high)
{
if (low < high)
{
int pivot = partition(arr, low, high); // 对表进行划分
quickSort(arr, low, pivot - 1);
quickSort(arr, pivot + 1, high);
}
}
快排在元素基本有序时会退化为冒泡排序,在有序时效率最低;快排是不稳定的算法。
希尔排序
希尔排序其实就是直接插入排序的升级版,步骤如下:
- 按照某种间隔(步长)首先对序列进行分组
- 对分好的组进行直接插入排序
- 缩小步长再次对序列进行分组,然后继续对新的分组进行直接插入排序,直到最后一次步长为1时,对全体元素进行直接插入排序
**注意:**希尔排序的整体框架基本不变,唯一影响到效率的就是步长了。
-
可以按照希尔本人提出的(1,2,4,8,16,32,64,…,2ⁿ)但是在最坏的情况下,该步长效率并不好!
-
对此有很多科学家提出了更加高效的步长选择方式。如Papernov和Stasevic在1965年提出的增量序列为(1,3,7,15,31,63,…,2ⁿ-1)可以将最坏情况改进至O(n³/²)
-
pratt于1971年提出(1,2,,3,4,6,8,9,12,16 … )各项除2和3外均不含其它素因子。最坏情况时间复杂度O(nlog²n)
-
尽管pratt序列的效率较高,但是其中各项的间距太小,会导致迭代趟数过多,因此Sedgewick综合Papernov-Stasevic序列与pratt序列的有点提出了(1,5,19,41,109,209,505,929,…)
其中各项,均为9 * 4ⁿ - 9 * 2ⁿ + 1或者4ⁿ - 3*2ⁿ + 1的形式,
改 进 之 后 最 坏 情 况 下 时 间 复 杂 度 为 O ( n 4 3 ) , 平 均 复 杂 度 O ( n 7 6 ) 改进之后最坏情况下时间复杂度为O(n^\frac{4}{3}),平均复杂度O(n^\frac{7}{6}) 改进之后最坏情况下时间复杂度为O(n34),平均复杂度O(n67)
在通常的应用环境中,这一增量序列综合效率最佳。
为方便演示代码,初始步长为数组长度/2,之后步长分别为当前步长/2,直到为1
template <typename T>
void shellSort(T arr[], int len)
{
for (int dis = len / 2; dis >= 1; dis /= 2) // 取步长方式
{
cout << "dis = " << dis << endl;
for (int i = dis; i < len; ++i) // 按分组进行直接插入排序
{
int j = i - dis; // 向后移动分组
T tmp = arr[i];
while (j >= 0 && tmp < arr[j])
{
arr[j + dis] = arr[j]; // 按步长向后移动元素
j -= dis;
}
arr[j + dis] = tmp; // 插入正确位置
}
}
}
堆排序
大根堆:所有的根节点大于等于叶子结点
小根堆:所有的根节点小于等于叶子结点
大根堆代码示例:
template <typename T>
void heapAdjust(T arr[], int loc, int len)
{
int child = 2 * loc + 1; // 位置为loc的根节点的左孩子
while (child + 1 < len) // 如果有孩子
{
if (arr[child] < arr[child + 1]) // 从左右孩子中选择最大的一个出来
{
++child;
}
// 将比根节点大的孩子与根节点交换,并更新根节点与孩子结点位置,进行下一次调整
if (arr[child] > arr[loc])
{
swap(arr[child], arr[loc]);
loc = child;
child = child * 2 + 1;
}
else
{
break;
}
}
}
template <typename T>
void heapSort(T arr[], int len)
{
// 初始建立大根堆,从最后一个元素开始向上调整
for (int i = len / 2 - 1; i >= 0; --i)
{
heapAdjust(arr, i, len);
}
// 将当前根节点与当前堆最后一个元素交换,然后重新调整堆(调整范围-1),
// 依次这样,直到全部调整完毕(范围为1)
for (int i = len - 1; i > 0; --i)
{
swap(arr[0], arr[i]);
heapAdjust(arr, 0, i);
}
}
归并排序
将两个或者两个以上的有序表合并为新的有序表。
template <typename T>
void merge(T arr[], int low, int mid, int high)
{
int i = low;
int j = mid + 1;
int k = 0;
// 辅助数组
T tmp[high - low + 1] = {0};
while (i <= mid && j <= high)
{
// 将小的元素元素存放在辅助数组当中
if (arr[i] <= arr[j])
{
tmp[k++] = arr[i++];
}
else
{
tmp[k++] = arr[j++];
}
}
// 如果mid的左边还有元素
while (i <= mid)
{
tmp[k++] = arr[i++];
}
// 如果mid的右边还有元素
while (j <= high)
{
tmp[k++] = arr[j++];
}
// 将辅助数组数据拷贝回原数组
for (int n = 0; n < high - low + 1; ++n)
{
arr[low + n] = tmp[n];
}
}
template <typename T>
void mergeSort(T arr[], int low, int high)
{
if (low < high)
{
// 二路归并
int mid = (high + low) / 2;
// 递归的归并
mergeSort(arr, low, mid);
mergeSort(arr, mid + 1, high);
merge(arr, low, mid, high);
}
}
基数排序
基数排序比较特殊,它不基于比较和移动进行排序,二是基于元素的各位的大小进行排序。通常分为:
- 最高位优先法(MSD):按照元素最高位到最低位依次逐层划分若干子序列,最后将所有子序列连接成一个有序的序列。
- 最低位优先法(LSD):按照元素的最低位到最高位依次进行排序。
最低位优先(LSD)代码:
void radixSort(int arr[], int len)
{
int cnt = 0;
int radix = 1; // 从个位开始排序
// 找到待排序列中的最大元素,然后根据最大元素的位数确定排序次数
int maxVal = arr[0];
for (int i = 1; i < len; ++i)
{
if (maxVal < arr[i])
{
maxVal = arr[i];
}
}
cout << "maxVal = " << maxVal << endl;
// 确定最大元素的位数
while (maxVal)
{
maxVal /= 10;
cnt++;
}
// 辅助数组,容量为10
vector<vector<int>> tmp(10);
cout << "tmp.capecity = " << sizeof(tmp) << endl;
// 由于最大元素位数为cnt,所以排序最多排cnt次
for (int i = 0; i < cnt; ++i)
{
// 清空tmp并分配大小
tmp.clear();
tmp.resize(10);
for (int i = 0; i < len; ++i)
{
int idx = (arr[i] / radix) % 10;
tmp[idx].push_back(arr[i]); // 按位存入数组中
}
// 对按位大小排序的元素重新排列
int k = 0;
for (auto vec : tmp)
{
for (auto elem : vec)
{
arr[k++] = elem;
}
}
// 下一位排序
radix *= 10;
}
}
总结
排序算法的性质
| 算法种类 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 简单选择排序 | 最好O(n²)、平均O(n²)、最坏O(n²) | O(1) | 不稳定 |
| 直接插入排序 | 最好O(n)、平均O(n²)、最坏O(n²) | O(1) | 稳定 |
| 冒泡排序 | 最好O(n)、平均O(n²)、最坏O(n²) | O(1) | 稳定 |
| 希尔排序 | 最好O(n)、平均O(n¹·³)、最坏O(n²) | O(1) | 不稳定 |
| 快速排序 | 最好O(n㏒₂n)、平均O(n㏒₂n)、最坏O(n²) | O(㏒₂n) | 不稳定 |
| 归并排序 | 最好O(n㏒₂n)、平均O(n㏒₂n)、最坏O(n㏒₂n) | O(n) | 稳定 |
| 堆排序 | 最好O(n㏒₂n)、平均O(n㏒₂n)、最坏O(n㏒₂n) | O(1) | 不稳定 |
| 基数排序 | 最好O(d(n+r))、平均O(d(n+r))、最坏O(d(n+r)) r代表关键字的基数,d代表长度,n代表关键字的个数 |
O® | 稳定 |
算法选择适用条件
- 当数据量较小时:可以采用直接插入或者简单选择排序,若要求稳定性可以选择直插,否则建议简单选择排序
- 当数据初始基本有序时:可选择直接插入或者冒泡排序
- 当数据量较大时:可以选择快排、堆排序、归并排序;在无规律数据时,快排的性能是比较好的,但如果不考虑辅助空间且要求稳定可以选择归并排序,可以配合直接插入排序来提高效率。
- 当数据量很大时、且元素位数较少可以分解,可以选择基数排序。