Linux内核数据结构 —— 无锁环形队列 ( kfifo )
1 初次见面
队列是常见的一种数据结构,简单看来就是一段数据缓存区,可以存储一定量的数据,先存进来的数据会被先取出,First In Fist Out,就是FIFO。
FIFO主要用于缓冲速度不匹配的通信。
例如生产者(数据产生者)可能在短时间内生成大量数据,导致消费者(数据使用方)无法立即处理完,那么就需要用到队列。生产者可以突然生成大量数据存到队列中,然后就去休息,消费者再有条不紊地将数据一条条取出解析。
FIFO示意图
再具体点的例子,通信接口驱动接收到通信数据时,需要将其存入队列,然后马上再回去接收或等待新数据,相关的通信解析程序只需要从队列中取数据即可。如果驱动每次接收到数据都要等待解析,则有可能导致新数据没能及时接收而丢失。
除了缓冲速度不匹配的通信外,FIFO也是“多生产者-单消费者”场景的一种解决方案。
2 简单了解
kfifo是linux内核的对队列功能的实现。在内核中,它被称为无锁环形队列。
所谓无锁,就是当只有一个生产者和只有一个消费者时,操作fifo不需要加锁。这是因为kfifo出队和入队时,不会改动到相同的变量。
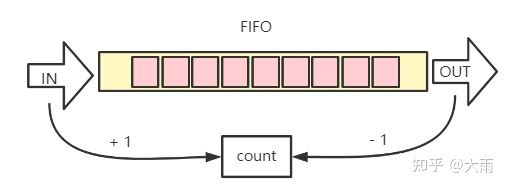
例如,如果让我们自己实现一个fifo,大家容易想到使用一个count来记录fifo中的数据量,入队一个则加一个,出队一个则减一个:
count计数
这种情况肯定是需要对count加锁的。那kfifo是怎么做的呢?
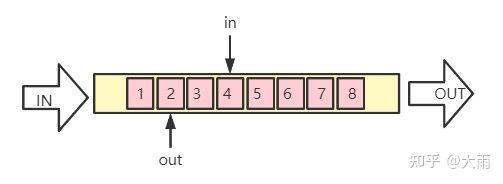
kfifo使用了in和out两个变量分别作为入队和出队的索引:
in&out索引
- 入队n个数据时,in变量就+n
- 出队k个数据时,out变量就+k
- out不允许大于in(out等于in时表示fifo为空)
- in不允许比out大超过fifo空间(比如上图,in最多比out多8,此时表示fifo已满)
如果in和out大于fifo空间了,比如上图中的8,会减去8后重新开始吗?
不,这两个索引会一直往前加,不轻易回头,为出入队操作省下了几个指令周期。
那入队和出队的数据从哪里开始存储/读取呢,我们第一时间会想到,把 in/out 用“%”对fifo大小取余就行了,是吧?
不,取余这种耗费资源的运算,内核开发者怎会轻易采用呢,kfifo的办法是,把 in/out 与上fifo->mask。这个mask等于fifo的空间大小减一(其要求fifo的空间必须是2的次方大小)。这个“与”操作可比取余操作快得多了。
由此,kfifo就实现了“无锁”“环形”队列。
了解了上述原理,我们就能意识到,这个无锁只是针对“单生产者-单消费者”而言的。“多生产者”时,则需要对入队操作进行加锁;同样的,“多消费者”时需要对出队操作进行加锁。
3 快速使用
kfifo主要有以下特点:
① 保证缓冲空间的大小为2的次幂,不是的向上取整为2的次幂。
② 使用无符号整数保存输入(in)和输出(out)的位置,在输入输出时不对in和out的值进行模运算,而让其自然溢出,并能够保证in-out的结果为缓冲区中已存放的数据长度,这也是最能体现kfifo实现技巧的地方;
③ 使用内存屏障(Memory Barrier)技术,实现单消费者和单生产者对kfifo的无锁并发访问,多个消费者、生产者的并发访问还是需要加锁的。
3.1 kfifo 的缓冲区大小必须为 2 的次幂
kfifo 要保证其缓存空间的大小为 2 的次幂,如果不是则向上取整为 2 的次幂。缓冲区大小取 2 的次幂的作用:
① 计算 (in) 和 (out) 的位置时,可以用"与运算"替代"取模运算",提高程序的运行效率。
② 使用无符号整数保存输入 (in) 和输出 (out) 的位置时,在输入输出时不对 (in) 和 (out) 的值进行模运算,而让其自然溢出,并能够保证 (in - out) 的结果为缓冲区中已存放的数据长度。
(1)判断一个数是不是 2 的次幂
kfifo 中对于 2 的次幂的判断方式非常巧妙。如果一个整数 x 是 2 的次幂,则二进制模式必然是 1000... ,而 x-1 的二进制模式则是 0111... ,也就是说 x 和 x-1 的每个二进制位都不相同,例如:8(1000) 和 7(0111); 若 x 不是 2 的次幂,则 x 和 x-1 的二进制必然有相同的位都为 1 的情况,例如:7(0111) 和 6(0110)。这样就可以根据 x & (x-1) 的结果来判断整数 x 是不是 2 的次幂,如下:
/*
判断x是否是2的幂
若x为2的次幂, 则 x & (x-1) == 0,也就是x和x-1的各个位都不相同。例如 8(1000)和7(0111)
若x不是2的次幂, 则 x & (x-1) != 0,也就是x和x-1的各个位肯定有相同的,例如7(0111)和6(0110)
*/
#define is_power_of_2(x) ((x) != 0 && (((x) & ((x) - 1)) == 0))(2) 将数字向上取整为2的次幂
如果设定的缓冲区大小不是 2 的次幂,则向上取整为 2 的次幂,例如:设定为 5,则向上取为 8。上面提到整数 n 是 2 的次幂,则其二进制模式为 100... ,故如果正数 k 不是 n 的次幂,只需找到其最高的有效位 1 所在的位置(从 1 开始计数)pos,然后 1 << pos 即可将 k 向上取整为 2 的次幂。实现如下:
#define roundup_pow_of_two(n) \
( \
__builtin_constant_p(n) ? ( \
(n == 1) ? 1 : \
(1UL << (ilog2((n) - 1) + 1)) \
) : \
__roundup_pow_of_two(n) \
)3.2 动态申请
动态申请步骤如下:
① 包含头文件 #include
② 定义一个 struct kfifo 变量;
③ 使用 kfifo_alloc 申请内存空间;
④ 分别使用 kfifo_in、kfifo_out 执行入队、出队的操作;
⑤ 不再使用kfifo时,使用 kfifo_free 释放申请的内存。
以下为一个最简的demo实现:
#include
//定义demo变量
struct demo_type {
struct kfifo fifo;
};
//定义fifo的元素(使用结构体是为了便于增删内容)
struct demo_element {
char val;
};
//定义fifo最大保存的元素个数
#define DM_FIFO_ELEMENT_MAX 32
//fifo句柄定义在全局,为了在不同的函数中进行出入队操作
static struct demo_type dm;
void demo(void)
{
int ret = 0;
struct demo_element element;
//申请fifo内存空间,一般在模块初始化时调用
ret = kfifo_alloc(dm.fifo, sizeof(struct demo_element)*DM_FIFO_ELEMENT_MAX, GFP_KERNEL);
if (ret) {
printk(KERN_ERR "kfifo_alloc fail ret=%d\n", ret);
return;
}
//入队
element.val = 111;
ret = kfifo_in(dm.fifo, &element, sizeof(struct demo_element));
if (!ret) {
printk(KERN_ERR "kfifo_in fail, fifo is full\n");
}
//出队
element.val = 0; //先清零,便于测试
ret = kfifo_out(dm.fifo, &element, sizeof(struct demo_element));
if (ret) {
printk(KERN_INFO "kfifo_out element.val=%d\n", element.val);
} else {
printk(KERN_ERR "kfifo_out fail, fifo is empty\n");
}
//释放内存空间,一般在模块退出时调用
kfifo_free(dm.fifo);
} 3.3 静态定义
静态定义步骤如下:
① 包含头文件 #include
② 使用宏 DECLARE_KFIFO 静态定义 fifo 变量;
③ 分别使用 kfifo_put、kfifo_get执行入队、出队的操作;
静态定义不需要申请和释放内存的步骤,出入队函数也更精简。
以下为一个最简的demo实现:
#include
//定义fifo的元素(使用结构体是为了便于增删内容)
struct demo_element {
char val;
};
//定义fifo最大保存的元素个数
#define DM_FIFO_ELEMENT_MAX 32
//静态定义已经包含了缓存定义
DECLARE_KFIFO(demo_fifo, struct demo_element, sizeof(struct demo_element)*DM_FIFO_ELEMENT_MAX);
void demo(void)
{
int ret = 0;
struct demo_element element;
//入队
element.val = 111;
ret = kfifo_put(demo_fifo, element); //注意这里的元素参数不是指针
if (!ret) {
printk(KERN_ERR "kfifo_put fail, fifo is full\n");
}
//出队
element.val = 0; //先清零,便于测试
ret = kfifo_get(demo_fifo, element); //注意这里的元素参数不是指针
if (ret) {
printk(KERN_INFO "kfifo_get element.val=%d\n", element.val);
} else {
printk(KERN_ERR "kfifo_get fail, fifo is empty\n");
}
} 3.4 其它常用API
//除上述两种定义方式外,还支持用户自己申请缓存,然后传递给fifo进行初始化:
kfifo_init(fifo, buffer, size)
//带锁的出入队
kfifo_in_locked(fifo, buf, n, lock)
kfifo_out_locked(fifo, buf, n, lock)
//获取队列的已有空间长度
kfifo_len(fifo)
//获取队列的空闲空间长度
kfifo_avail(fifo)
//判断队列是否为空
kfifo_is_empty(fifo)
//判断队列是否为满
kfifo_is_full(fifo)
//清空队列
kfifo_reset(fifo)4 读读源码
kfifo 在源码中的相对路径是:
① lib/kfifo.c
② include/linux/kfifo.h
官网地址(4.14 版本):Linux source code (v4.14) - Bootlin
最后再看看kfifo的几段精华代码。
4.1 结构体
首先看一眼kfifo的结构体:
struct __kfifo {
unsigned int in; /* 入队索引 */
unsigned int out; /* 出队索引 */
unsigned int mask; /* 大小掩码 */
unsigned int esize; /* 单个元素大小 */
void *data; /* 队列缓存指针 */
};4.2 内存申请
这个就是kfifo申请内存顺便初始化的过程。
int __kfifo_alloc(struct __kfifo *fifo, unsigned int size,
size_t esize, gfp_t gfp_mask)
{
/*
* round down to the next power of 2, since our 'let the indices
* wrap' technique works only in this case.
*/
size = roundup_pow_of_two(size);
fifo->in = 0;
fifo->out = 0;
fifo->esize = esize;
if (size < 2) {
fifo->data = NULL;
fifo->mask = 0;
return -EINVAL;
}
fifo->data = kmalloc(size * esize, gfp_mask);
if (!fifo->data) {
fifo->mask = 0;
return -ENOMEM;
}
fifo->mask = size - 1;
return 0;
}
EXPORT_SYMBOL(__kfifo_alloc);我们看第31行,发现kfifo最终申请的内存空间,是调用者要求空间的向上取2的次方。比如想申请7字节,最终是申请8字节;想申请9字节,最终是申请16字节。
这样才能实现用mask大小掩码“与”上in/out索引,实现队列回环(避免取余计算)。
如果使用者不了解这个规则,则可能会踩坑。比如某个程序想申请100字节,但实际申请到的是128字节而不自知。假设这个程序每次入队和出队都是10字节,当fifo存满后,最后一次入队的10字节实际上只保存了8字节,此后每次还是按10字节出队的话,则会永远错位2字节。
4.3 入队操作
unsigned int __kfifo_in(struct __kfifo *fifo,
const void *buf, unsigned int len)
{
unsigned int l;
l = kfifo_unused(fifo);
if (len > l)
len = l;
kfifo_copy_in(fifo, buf, len, fifo->in);
fifo->in += len;
return len;
}
EXPORT_SYMBOL(__kfifo_in);buffer 已用的空间是 in - out,总空间是 mask + 1。入队共3个步骤:
① 查询剩余空间(确认最大可入队的长度)
② 拷贝数据进内存
③ in 索引更新
注意:这里只是用了 fifo->in += len 而未取模,用到了无符号整型变量的溢出性质,当 in 持续增加到溢出时又会被置为 0。参考章节"5 kfifo 处理溢出的方法"。
/*
* internal helper to calculate the unused elements in a fifo
*/
static inline unsigned int kfifo_unused(struct __kfifo *fifo)
{
return (fifo->mask + 1) - (fifo->in - fifo->out);
}拷贝数据函数如下:
static void kfifo_copy_in(struct __kfifo *fifo, const void *src,
unsigned int len, unsigned int off)
{
unsigned int size = fifo->mask + 1;
unsigned int esize = fifo->esize;
unsigned int l;
off &= fifo->mask;
if (esize != 1) {
off *= esize;
size *= esize;
len *= esize;
}
l = min(len, size - off);
memcpy(fifo->data + off, src, l);
memcpy(fifo->data, src + l, len - l);
/*
* make sure that the data in the fifo is up to date before
* incrementing the fifo->in index counter
*/
smp_wmb();
}首先是确定入队的内存地址 off(通过 &mask 获得,前提是size 必须为 2 的次幂),esize是元素大小。其中 (size - off) 表示从插入位置 off 到到 buffer 末尾所剩余的长度,l 取 len 和剩余长度的最小值。
调用 memcpy 函数拷贝 l 字节到 (fifo->data + off) 的位置上,如果 l = len,即拷贝完成,len - l = 0,那么接下来的 memcpy 函数将不会执行;如果 l = size - off,接下来的 memcpy 函数还需要把剩下的 len – l 长度拷贝到 buffer 的头部。最后还有一句写内存屏障 smp_wmb(),确保内存拷贝在in索引更新前完成,避免出现乱序异常。
5 kfifo 处理溢出的方法
(1)队列溢出
① 空的 kfifo
② kfifo_in 一个 buffer 后
③ kfifo_out 一个 buffer 后
④ 当此时put的buffer长度超出in到末尾长度时,则将剩下的移到头部去
前三种情况下从图中可以很清晰的看出 in - out 为缓冲区中的已有的数据长度,但是最后一种发现 in 跑到了 out 的前面,这时候 in - out 不是应该为负的么,怎么能是数据长度?这正是 kfifo 的高明之处,in 和 out 都是无符号整数,那么在 in < out 时 in - out 就是负数,把这个负数当作无符号来看时,其值仍然是缓冲区中的数据长度。这和 in 累加到溢出的情况基本一致,这里放在一起说。
这里使用 8 位无符号整数来保存 in 和 out ,方便溢出。这里假设 out = 100,in = 255,size = 256,如下图:
/*
--------------------------------------
| | | |
--------------------------------------
out = 100 in = 250
这时缓冲区中已有的数据为:in - out = 150,空闲空间为:size - (in - out) = 106
向缓冲区中put10个数据后
--------------------------------------
| | | |
--------------------------------------
in out
这时候 in + 10 = 260 溢出变为in = 4;这是 in - out = 4 - 100 = -96,
仍然溢出-96十六进制为`0xA0`,将其直接转换为有符号数`0xA0 = 160`,
在没put之前的数据为150,put10个后,缓冲区中的数据刚好为160,刚好为溢出计算结果。
*/进行上述运算的前提是,size 必须为 2 的次幂。假如 size = 257,则上述的运行就不会成功。为什么 size 一定要为 2 的次幂才可以进行上述运算?我猜测应该和 in(out) 的类型都是 2 的次幂有关。
( 以上图片引用自:Linux内核数据结构之kfifo )
6 参考
kfifo(linux kernel 无锁队列) - 知乎 (zhihu.com)
(1条消息) 眉目传情之匠心独运的kfifo_chen19870707的博客-CSDN博客
模仿Linux内核kfifo实现的循环缓存_Linux编程_Linux公社-Linux系统门户网站 (linuxidc.com)