机器学习 | 聚类问题

一、K均值聚类

这里我们用鸢尾花数据及进行聚类分析，这种含有标签数据的数据集，只要不调用标签数据，就可以为无监督学习所采用。鸢尾花数据具有4个特征，为了可视化这里选取前两个特征进行聚类分析并指定聚为3类。

#导入库
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
#### 默认设置下matplotlib图片清晰度不够，可以将图设置成矢量格式
%config InlineBackend.figure_format='svg'
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris

#记载数据
data=load_iris()
x=data.data
X=x[:,:2]

#构建模型及预测
model=KMeans(n_clusters=3)  #调用KMeans模型并指定聚为3类
model.fit(X)  #对数据进行学习
y_pred=model.predict(X)  #预测结果
print(y_pred)  #输出标签的预测结果

#画图
fig,ax=plt.subplots(1,2)
plt.subplot(1,2,1)
plt.scatter(X[:,0],X[:,1])  #将构建的数据点画出
plt.xlabel("Sepal Length")  #x轴标签
plt.ylabel("Sepal Width")  #y轴标签

plt.subplot(1,2,2)  #画子图2
plt.scatter(X[:,0],X[:,1],c=y_pred)  #经过聚类后的散点图
plt.scatter(model.cluster_centers_[:,0],model.cluster_centers_[:,1],
           marker='*',c='r',linewidth=7)  #画出中心点
plt.xlabel("Sepal Length")
plt.ylabel("Sepal Width")
#调整子图的间距
plt.subplots_adjust(left=None,bottom=None,right=None,
                  top=None,wspace=0.5,hspace=None)
plt.show()

 尽管都属于超参数，需要人为设置，但K均值聚类中的K与k近邻算法中的k明显不同。

在k近邻算法中，由于是分类问题，这种监督学习的类别数是早已知晓的，其k的含义是选择k个样本点参与“投票”，而K均值聚类中的K则是将数据聚为k类，此时的K决定了结果中的类别数量。

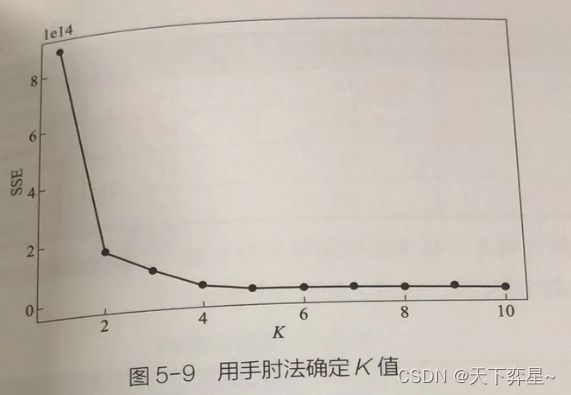
选择聚类问题中的K值，最佳的取值可以利用手肘法进行评估，它是一种用于确定数据集中聚类数量的启发式算法。

import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
#### 默认设置下matplotlib图片清晰度不够，可以将图设置成矢量格式
%config InlineBackend.figure_format='svg'
%matplotlib inline

rd=pd.read_csv('regional data.csv')
X=rd.iloc[:,1]

K=[]  #空列表
Score=[]  #空列表
for k in range(1,11):
    kmeans=KMeans(n_clusters=k)
    kmeans.fit(X)
    score=kmeans.interia_  #整体平方和
    K.append(k)  #空列表追加赋值
    Score.append(score)  #空列表追加赋值
plt.plot(K,Score,marker='o')  #画图
plt.xlabel('K')  #x轴标签
plt.ylabel('SSE')  #y轴标签
plt.show()

图中横轴为K的取值，因为数据集有10个特征，因此取值从1至10。纵轴是 误差平方和，它是所有样本的聚类误差，是衡量聚类效果优劣的一个指标。图中折线下降最快的K值称为手肘部，当K从4开始折线趋于平缓，我们认为进行K均值聚类时，K应该设置为4。

二、系统聚类

系统聚类是聚类分析中最常用的方法之一。它的基本思路是：先将每个样本视为一类，然后计算类与类之间的距离并按照一定的准则将两类合并为新类，依此类推，直到一步步将所有的样本归为一类后聚类终止。

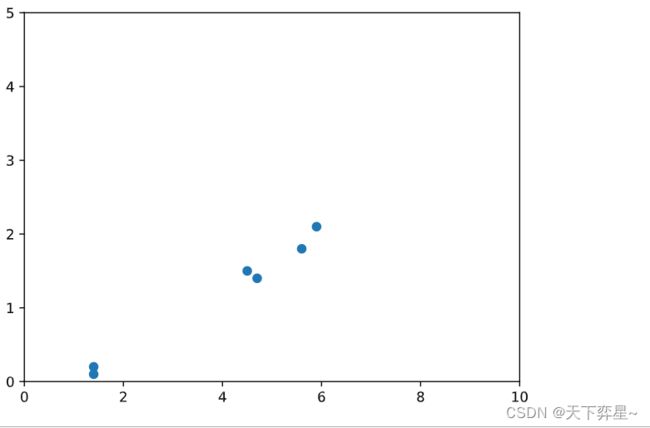
首先输入6个样本点并给出散点图。

import numpy as np
from matplotlib import pyplot as plt
#### 默认设置下matplotlib图片清晰度不够，可以将图设置成矢量格式
%config InlineBackend.figure_format='svg'
from scipy.cluster.hierarchy import dendrogram,linkage
data=np.array([[1.4,0.2],[1.4,0.1],[4.7,1.4],[4.5,1.5],[5.9,2.1],[5.6,1.8]])
plt.scatter(data[:,0],data[:,1])
plt.ylim([0,5])  #设置纵轴数值范围
plt.xlim([0,10])  #设置横轴数值范围
plt.show()

下面的代码中，我们利用参数single（最短距离法）进行距离的计算，根据时间情况的需要，我们还可以选择average（类平均法）、complete（最长距离法）、ward（瓦尔德法）等方法进行系统聚类。

Dist_data=linkage(data,"single")  #用single法计算距离
print(Dist_data)

聚焦第一行：前两个值代表“类”，Python从0开始计数，最初每个数据点各为一类，所以0和1这两个数据点表示为两类，第三个数字0.1就是0和1两个点的距离，这两个点被合并为一个类，第四个数字2表示该类中含有两个子类。

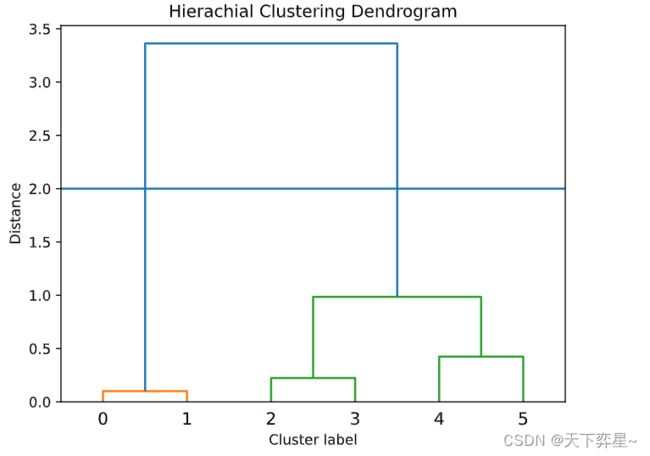
聚类完成后，还可以画出系统聚类树状图进行观察，代码如下：

dendrogram(Dist_data)  #画图
plt.title("Hierachial Clustering Dendrogram")
plt.xlabel("Cluster label")
plt.ylabel("Distance")
plt.axhline(y=2)  #给出指定的分类线
plt.show()

上图中，横轴表示类别标签，纵轴表示并类距离，是之前求得的类间距距离。从上图中很容易看到各成一类的数据是如何一步步汇聚成一个大类的。

综上，系统聚类的全部代码如下：

import numpy as np
from matplotlib import pyplot as plt
#### 默认设置下matplotlib图片清晰度不够，可以将图设置成矢量格式
%config InlineBackend.figure_format='svg'
from scipy.cluster.hierarchy import dendrogram,linkage
data=np.array([[1.4,0.2],[1.4,0.1],[4.7,1.4],[4.5,1.5],[5.9,2.1],[5.6,1.8]])
plt.scatter(data[:,0],data[:,1])
plt.ylim([0,5])  #设置纵轴数值范围
plt.xlim([0,10])  #设置横轴数值范围
plt.show()

#进行系统聚类
Dist_data=linkage(data,"single")  #用single法计算距离
print(Dist_data)

#画出系统聚类树状图
dendrogram(Dist_data)  #画图
plt.title("Hierachial Clustering Dendrogram")
plt.xlabel("Cluster label")
plt.ylabel("Distance")
plt.axhline(y=2)  #给出指定的分类线
plt.show()