算法Day20 | 654.最大二叉树, 617.合并二叉树, 700.二叉搜索树中的搜索, 98.验证二叉搜索树
Day20
-
- 654.最大二叉树
- 617.合并二叉树
- 700.二叉搜索树中的搜索
- 98.验证二叉搜索树
654.最大二叉树
题目链接: 654.最大二叉树
递归终止条件一定要先写出来。 终止条件选好,可以省略很多多余的代码
构造二叉树题目,要用前序遍历。因为先构造中节点,再构造左右节点。
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
if (nums.empty()) return nullptr;//终止条件
int maxValue = nums[0], maxIndex = 0;
for (int i = 0; i < nums.size(); ++i) {
nums[i] > maxValue ? maxValue = nums[i], maxIndex = i : int{};
}
auto root = new TreeNode(maxValue);//中
vector<int> left(nums.begin(), nums.begin() + maxIndex);
root->left = constructMaximumBinaryTree(left);//左
vector<int> right(nums.begin() + maxIndex + 1, nums.end());
root->right = constructMaximumBinaryTree(right);//右
return root;
}
};
用std::max_element()算法。当然,本质和上述代码没区别。
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
if (nums.empty()) return nullptr;
auto maxIter = max_element(nums.begin(), nums.end());
auto root = new TreeNode(*maxIter);
vector<int> left(nums.begin(), maxIter);
root->left = constructMaximumBinaryTree(left);
vector<int> right(maxIter + 1, nums.end());
root->right = constructMaximumBinaryTree(right);
return root;
}
};
上述两部分代码有点消耗资源,每次递归都要重新构建新的数组。可以将递归函数形参改为数组下标,即只对初始数组进行修改。
class Solution {
public:
TreeNode* recursion(vector<int>& nums, int startIndex, int endIndex) {
if (endIndex == startIndex) return nullptr;//终止条件
int maxValue = nums[startIndex], maxIndex = startIndex;
for (int i = startIndex; i < endIndex; ++i) {
nums[i] > maxValue ? maxValue = nums[i], maxIndex = i : int{};
}
auto cur = new TreeNode(maxValue);
cur->left = recursion(nums, startIndex, maxIndex);
cur->right = recursion(nums, maxIndex + 1, endIndex);
return cur;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return recursion(nums, 0, nums.size());
}
};
617.合并二叉树
题目链接: 617.合并二叉树
终止条件的选择,可以减少判断
递归
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (!root1) return root2;
if (!root2) return root1;
auto root = new TreeNode(root1->val + root2->val);
root->left = mergeTrees(root1->left, root2->left);
root->right = mergeTrees(root1->right, root2->right);
return root;
}
};
if (!root1) return root2;
if (!root2) return root1;
if (!root1 && !root2) return nullptr;
前两条if判断,比第三条if判断范围更广。
上述代码,需要重新构建一个新的节点。可以将原有节点最为新的节点来使用。
递归
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (!root1) return root2;
if (!root2) return root1;
root1->val += root2->val;
root1->left = mergeTrees(root1->left, root2->left);
root1->right = mergeTrees(root1->right, root2->right);
return root1;
}
};
迭代 层序遍历
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (!root1) return root2;
if (!root2) return root1;
queue<TreeNode*> que;
que.push(root1);
que.push(root2);
while (!que.empty()) {
auto cur1 = que.front();que.pop();
auto cur2 = que.front();que.pop();
cur1->val += cur2->val;
if (cur1->left && cur2->left) {
que.push(cur1->left);
que.push(cur2->left);
}
if (cur1->right && cur2->right) {
que.push(cur1->right);
que.push(cur2->right);
}
if (!cur1->left && cur2->left) cur1->left = cur2->left;
if (!cur1->right && cur2->right) cur1->right = cur2->right;
}
return root1;
}
};
700.二叉搜索树中的搜索
题目链接: 700.二叉搜索树中的搜索
递归
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if (!root || root->val == val) return root;
return val < root->val ? searchBST(root->left, val) :
searchBST(root->right, val);
}
};
迭代
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
while (root && root->val != val) {
root = root->val > val ? root->left : root->right;
}
return root;
}
};
上述两部分代码,有一个隐形操作,if(!root) return nullptr 改成 if(!root) return root 。
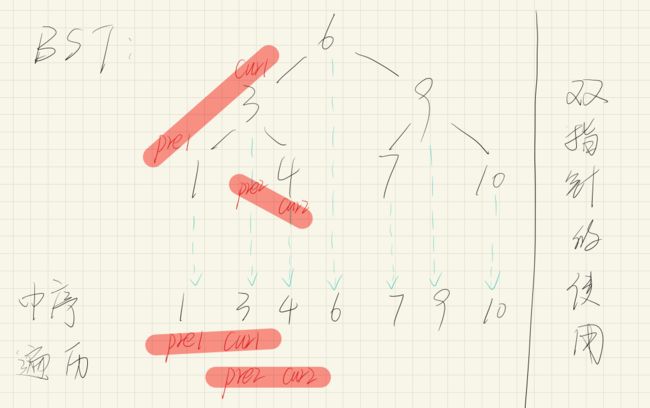
98.验证二叉搜索树
题目链接: 98.验证二叉搜索树
如果是深度遍历,先确定是前中后序遍历哪一个。搜索二叉树,用中序遍历做,用中序遍历才能使用好BST的特性。
class Solution {
public:
long maxValue = LONG_MIN;//按题目要求可得
bool isValidBST(TreeNode* root) {
if (!root) return true;
bool left = isValidBST(root->left);
if (root->val > maxValue) {
maxValue = root->val;
} else return false;
bool right = isValidBST(root->right);
return left && right;
}
};
下述代码不用根据题意来设置最小值。不用是面向测试的编程
class Solution {
public:
TreeNode* pre = nullptr;//root的前一个指针
bool isValidBST(TreeNode* root) {
if (!root) return true;
bool left = isValidBST(root->left);
if (pre && pre->val >= root->val) return false;
pre = root; //pre指针移动
bool right = isValidBST(root->right);
return left && right;
}
};