python——Dijkstra最短路径（以一组具体的数据为例，也可以输入一组数据。有向图）

一、Dijkstra

基本原理：

            按照最短路径递增的次序，逐次搜索出从起点到网络中其余所有点的最短路径。

• 给出从一条起点到终点的初始路径；
• 对这条路径不断的优化，使其距离减小；
• 当不能再被优化时，即为最短路径。

基本思想：设置一个集合S存放已经找到最短路径的顶点，S的初始状态只包含源点v，对vi∈V-S，假设从源点v到vi的有向边为最短路径。  以后每求得一条最短路径v, …, vk，就将vk加入集合S中，并将路径v, …, vk , vi与原来的假设相比较，取路径长度较小者为最短路径。重复上述过程，直到集合V中全部顶点加入到集合S中。

二、以一个实例来助于理解

如图是有向图，我们根据有的数据（顶点号，临接号，权值）画出有向图，然后根据有向图写出图的矩阵表示。

其中A,B,C,D,F,G,H分别用0,1,2,3,4,5,6,7表示。

从以上数据我们可以得到数据中：图的顶点有8个，顶点之间用有向线连接的有15条线段。

三、python代码

'''
顶点 A B C D E F G H
     0 1 2 3 4 5 6 7
A—F表示顶点号，分别用数字0,1,2,3,4,5,6,7代替；
顶点号，临接号，权值
0,1,1
0,2,4
0,3,4
1,2,2
1,4,9
2,4,6
2,5,3
2,6,4
2,3,3
3,6,7
4,7,1
5,4,2
5,7,5
6,5,1
6,7,3

'''
import sys
# 定义不可达距离
max=sys.maxsize

# points点个数，edges边个数,graph路径连通图的矩阵表示,start起点,end终点
def Dijkstra(points, edges, graph, start, end):
    map = [[max for i in range(points )] for j in range(points)]
    pre = [0] * (points)  # 记录前驱
    vis = [0] * (points)  # 记录节点遍历状态
    distance = [max for i in range(points )]  # 保存最短距离
    road = [0] * (points )  # 保存最短路径
    map = graph


    for i in range(points):  # 初始化起点到其他点的距离
        if i == start:
            distance[i] = 0
        else:
            distance[i] = map[start][i]
        if map[start][i] != max:
            pre[i] = start
        else:
            pre[i] = -1
    vis[start] = 1
    for i in range(points):  # 每循环一次确定一条最短路
        min = max
        for j in range(points):  # 寻找当前最短路
            if vis[j] == 0 and distance[j] < min:
                t = j
                min = distance[j]
        vis[t] = 1  # 找到最短的一条路径 ,标记
        for j in range(points ):
            if vis[j] == 0 and distance[j] > distance[t] + map[t][j]:
                distance[j] = distance[t] + map[t][j]#更新最短路径
                pre[j] = t
    #print(distance)
    p = end
    leng = 0
    while p >= 1 and leng < points:
        road[leng] = p
        p = pre[p]
        leng += 1
    leng -= 1
    while leng >= 0:
        road.append(road[leng])
        leng -= 1

    path_1 = list()
    for i in range(len(road)):
        if road[i] != road[i + 1]:
            path_1.append(road[i])
        else:
            path_1.append(road[i])
            break
    path_2 = list()
    for j in range(len(path_1)):
        path_2.append(path_1.pop())



    return distance[end], path_2


# 固定map图
def map():
'''若想给为其它的有向图那么需要将map数组该为你的图的矩阵，将下面的顶点8和边15改为你图的顶点和边数边数就是你数据的个数。'''

    map = [
        [0, 1, 4, 4, max, max,max,max],
        [max, 0, 2,max, 9, max,max, max],
        [max, max, 0, 3, 6,3,4, max],
        [max, max, max, 0,max, max, 7,max],
        [max, max, max, max, 0,max,max,1],
        [max, max, max, max, 2,0,max, 5],
        [max,max,max,max,max,1,0,3],
        [max,max,max,max,max,max,max,0]
        ]

    start, end = input("输入起点和终点：").split()
    distance, road = Dijkstra(8, 15, map, int(start), int(end))
    print("最短距离：", distance)
    print("最短路径(经过的点号)：", road)


#输入边关系构造map图
def createmap():
    a, b = input("输入节点数和边数：").split()
    n = int(a)
    m = int(b)
    map = [[max for i in range(n + 1)] for j in range(n + 1)]
    for i in range(m):
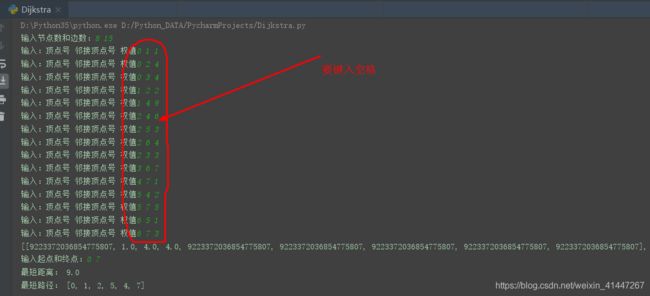
        x, y, z = input("输入：顶点号 邻接顶点号 权值")#.split()#注释split（）为了输入快，若有高位时还是保留split（），这时候输入一个数据需要打入一个空格。
        point = int(x)
        edge = int(y)
        map[point][edge] = float(z)
        map[edge][point] = float(z)
    print(map)
    s, e = input("输入起点和终点：").split()
    start = int(s)
    end = int(e)
    dis, road = Dijkstra(n, m, map, start, end)
    print("最短距离：", dis)
    print("最短路径：", road)


if __name__ == '__main__':
   map()
   #createmap()#这个是输入数据直接建立图的矩阵，从而求最短路径。这个和map要分开执行。

四、运行效果

1、

2.1

这是注释掉split（）后的输入效果。

2.2这是没有注释split()的输入效果

五、总结

Dijkstra算法还是比较不好理解的，完成这个程序还是费了不小的精力。

本程序中固定图是自己键入图的矩阵，这是比较要大的键入过程。

createmap()时是比较有些问题的，如求2到5的最短路径是，给出的路径的第一个点始终是0，那么这是不对的，所以当求出这个路径了，要忽略路径第一个数。这是程序需要优化的地方。

还有的缺点就是，当给的数据量是非常大的时候，固定图是不适合的，你不可能将这个矩阵慢慢的列出来吧。

那么createmap的优势就来了，可以对具有大数据量的顶点的图进行处理，当然像上面的一个一个数据的输入也是不太现实的，一两百个都还算好的，当有一亿或更多的这数据，你也一个个的输入吗。当然是no，所以我们可以改进为读取文本的方式来获得数据，这样就不用一个一个的输入数据了。有兴趣可以试一下，这是很简单的，知道怎么读取文件就行了。

---

                                                                                                                                                              作者：诚长ing

---