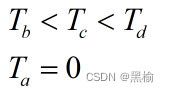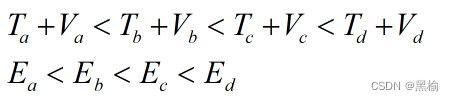通过自由度比较迭代次数
( A, B )---3*30*2---( 1, 0 )( 0, 1 )
让网络的输入只有3个节点,AB训练集各由5张二值化的图片组成,让A中有7个1,B中全是0,让A的5行1的数量为1,1,1,2,2;让A的3列1的数量为2,2,3.排列组合A,比较迭代次数的顺序。
| 差值结构 |
A-B |
迭代次数 |
行 |
列 |
|||||||||||
| d |
1 |
1 |
0 |
6*3*2*1*4-0*0*0*0*0 |
3124.859 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
||
| 0 |
1 |
1 |
6*3*2*1*4-0*0*0*0*0 |
3124.859 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 0 |
1 |
0 |
6*3*2*1*4-0*0*0*0*0 |
3124.859 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 0 |
0 |
1 |
6*3*2*1*4-0*0*0*0*0 |
3124.859 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 1 |
0 |
0 |
6*3*2*1*4-0*0*0*0*0 |
3124.859 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
||||||||
| c |
1 |
1 |
0 |
6*4*3*1*4-0*0*0*0*0 |
7107.332 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
||
| 1 |
0 |
0 |
6*4*3*1*4-0*0*0*0*0 |
7107.332 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 0 |
1 |
1 |
6*4*3*1*4-0*0*0*0*0 |
7107.332 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 0 |
0 |
1 |
6*4*3*1*4-0*0*0*0*0 |
7107.332 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 1 |
0 |
0 |
6*4*3*1*4-0*0*0*0*0 |
7107.332 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
||||||||
| b |
1 |
1 |
0 |
6*6*1*1*2-0*0*0*0*0 |
9197.935 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
||
| 1 |
1 |
0 |
6*6*1*1*2-0*0*0*0*0 |
9197.935 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 0 |
0 |
1 |
6*6*1*1*2-0*0*0*0*0 |
9197.935 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 0 |
0 |
1 |
6*6*1*1*2-0*0*0*0*0 |
9197.935 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 0 |
1 |
0 |
6*6*1*1*2-0*0*0*0*0 |
9197.935 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
||||||||
| a |
1 |
0 |
0 |
4*4*4*3*3-0*0*0*0*0 |
26733.89 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
||
| 1 |
0 |
0 |
4*4*4*3*3-0*0*0*0*0 |
26733.89 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 1 |
0 |
0 |
4*4*4*3*3-0*0*0*0*0 |
26733.89 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 0 |
1 |
1 |
4*4*4*3*3-0*0*0*0*0 |
26733.89 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 0 |
1 |
1 |
4*4*4*3*3-0*0*0*0*0 |
26733.89 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
|||
| 1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
||||||||
| 1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
||||||||
收敛误差7e-4,每组收敛199次。统计平均值。
因为符合上述条件的差值结构的行和列可以自由变换,按照对称性只有4个不同的结构。
迭代次数的大小顺序是a>b>c>d.
这4个结构的平均列都相同,所以这4个结构的势能相同,
但他们的迭代次数并不相同。这意味着还有一个变量导致了总能量的差异。
现在让a保持行分布1,1,1,2,2;列分布2,2,3不变,让a变化1步
| a |
a |
a |
a |
a |
b |
|||||||||||||||||
| 1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|||||
| 1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|||||
| 1 |
0 |
0 |
→ |
1 |
0 |
0 |
→ |
1 |
0 |
0 |
→ |
0 |
1 |
0 |
→ |
0 |
0 |
1 |
→ |
0 |
0 |
1 |
| 0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|||||
| 0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|||||
| a |
c |
c |
c |
c |
c |
|||||||||||||||||
| 1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|||||
| 1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
|||||
| 1 |
0 |
0 |
→ |
1 |
0 |
1 |
→ |
0 |
1 |
0 |
→ |
1 |
0 |
0 |
→ |
1 |
0 |
0 |
→ |
0 |
1 |
1 |
| 0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|||||
| 0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
由于对称性a只有两种可能的变化,一种横着走一步,变成b,或者竖着走一步变成c。但a在一步内不可能变成d。
但是b或c都可以1步变成d
| c |
d |
|||||||||
| 1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
||
| 1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
||
| 0 |
1 |
1 |
→ |
1 |
0 |
0 |
→ |
0 |
1 |
0 |
| 0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
||
| 1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
||
| b |
d | d |
||||||||
| 1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
||
| 1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
||
| 0 |
0 |
1 |
→ |
0 |
1 |
1 |
→ |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
||
| 0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
也就是a距离d至少有两步。比如假设横向移动1步的能量小于纵向移动一步的能量,则由a变化到b,c,d的能量排序b 所以得到总能量 迭代次数与结构的总能量成反比,总能量越低成键越稳定,使键断裂的难度越大,迭代次数越大。