BP推导,普通版加矩阵版
BP推导,普通版加矩阵版
- 普通版
-
- 前向传播过程
- 反向传播过程
- 矩阵版
前向传播用来计算整个卷积过程的输出值以及相应的误差值。反向传播则是想把误差值平摊至每个参数上,使得最终的输出值越来越逼近标签值。
普通版
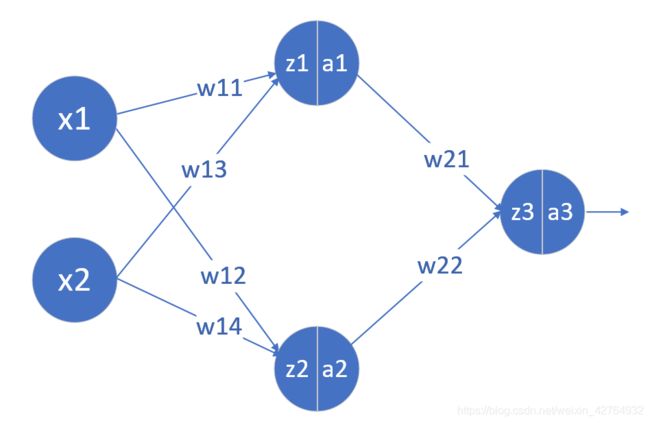
前向传播过程
如下:
激活函数为sigmoid δ ( x ) = 1 1 + e − x \delta(x) = \frac{1}{1+e^{-x}} δ(x)=1+e−x1
第一层
z 1 = w 11 x 1 + w 13 x 2 + b 1 a 1 = δ ( z 1 ) z_1 = w_{11}x_1 + w_{13}x_2 + b_1\\ \\a_1=\delta(z_1) z1=w11x1+w13x2+b1a1=δ(z1)
z 2 = w 12 x 1 + w 14 x 2 + b 2 a 2 = δ ( z 2 ) z_2 = w_{12}x_1 + w_{14}x_2 + b_2\\ \\a_2=\delta(z_2) z2=w12x1+w14x2+b2a2=δ(z2)
第二层
z 3 = w 21 a 1 + w 22 a 2 + b 3 a 3 = δ ( z 3 ) z_3 = w_{21}a_1 + w_{22}a_2 + b_3\\ \\a_3=\delta(z_3) z3=w21a1+w22a2+b3a3=δ(z3)
反向传播过程
已知激活函数为sigmoid δ ( x ) = 1 1 + e − x \delta(x) = \frac{1}{1+e^{-x}} δ(x)=1+e−x1
该激活函数的导函数为 δ ′ ( x ) = δ ( x ) ( 1 − δ ( x ) ) \delta^{'}(x) = \delta(x)(1-\delta(x)) δ′(x)=δ(x)(1−δ(x))
损失函数定义为MSE均方值损失 E = 1 2 ( y − a 3 ) 2 E=\frac{1}{2}(y-a_3)^2 E=21(y−a3)2
根据梯度下降法,令损失函数对参数求导,并更新 w = w − η ⋅ Δ w w = w - \eta \cdot \Delta w w=w−η⋅Δw
具体如下:
第二层参数
Δ w 21 = ∂ E ∂ w 21 = ∂ E ∂ a 3 ⋅ ∂ a 3 ∂ z 3 ⋅ ∂ z 3 ∂ w 21 = − ( y − a 3 ) ⋅ a 3 ( 1 − a 3 ) ⋅ a 1 = g 21 ⋅ a 1 \Delta w_{21} = \frac{\partial E}{\partial w_{21}} =\frac{\partial E}{\partial a_{3}} \cdot \frac{\partial a_{3}}{\partial z_{3}} \cdot \frac{\partial z_{3}}{\partial w_{21}} \\\ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =- ( y - a _ { 3 } ) \cdot a _ { 3 } ( 1 - a _ { 3 } ) \cdot a _ { 1 } \\ \ \\ \ \ \ \ \ \ = g _ { 2 1 } \cdot a _ { 1 } Δw21=∂w21∂E=∂a3∂E⋅∂z3∂a3⋅∂w21∂z3 =−(y−a3)⋅a3(1−a3)⋅a1 =g21⋅a1
Δ w 22 = ∂ E ∂ w 22 = ∂ E ∂ a 3 ⋅ ∂ a 3 ∂ z 3 ⋅ ∂ z 3 ∂ w 22 = g 21 ⋅ a 2 \Delta w_{22} = \frac{\partial E}{\partial w_{22}} = \frac{\partial E}{\partial a_{3}} \cdot \frac{\partial a_{3}}{\partial z_{3}} \cdot \frac{\partial z_{3}}{\partial w_{22}} \\ \ \\ = g _ { 2 1 } \cdot a _ { 2 } Δw22=∂w22∂E=∂a3∂E⋅∂z3∂a3⋅∂w22∂z3 =g21⋅a2
Δ b 3 = ∂ E ∂ b 3 = ∂ E ∂ a 3 ⋅ ∂ a 3 ∂ z 3 ⋅ ∂ z 3 ∂ b 3 = g 21 \Delta b_3 = \frac{\partial E}{\partial b_{3}} = \frac{\partial E}{\partial a_{3}} \cdot \frac{\partial a_{3}}{\partial z_{3}} \cdot \frac{\partial z_{3}}{\partial b_{3}} \\ \ \\ = g_{21} Δb3=∂b3∂E=∂a3∂E⋅∂z3∂a3⋅∂b3∂z3 =g21
记 g 21 = − ( y − a 3 ) ⋅ a 3 ( 1 − a 3 ) g_{21} = - ( y - a _ { 3 } ) \cdot a _ { 3 } ( 1 - a _ { 3 } ) g21=−(y−a3)⋅a3(1−a3)
第一层参数
Δ w 11 = ∂ E ∂ w 11 = ∂ E ∂ a 3 ⋅ ∂ a 3 ∂ z 3 ⋅ ∂ z 3 ∂ a 1 ⋅ ∂ a 1 ∂ z 1 ⋅ ∂ z 1 ∂ w 11 = g 21 ⋅ w 21 a 1 ( 1 − a 1 ) ⋅ x 1 = g 21 ⋅ g 11 ⋅ x 1 \Delta w_{11} = \frac{\partial E}{\partial w_{11}} =\frac{\partial E}{\partial a_{3}} \cdot \frac{\partial a_{3}}{\partial z_{3}} \cdot \frac{\partial z_{3}}{\partial a_{1}}\cdot \frac{\partial a_{1}}{\partial z_{1}}\cdot \frac{\partial z_{1}}{\partial w_{11}} \\\ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =g _ { 21 } \cdot w_{21} a _ { 1 } ( 1 - a _ {1 } ) \cdot x _ { 1 } \\ \ \\ \ \ \ \ \ \ = g _ { 2 1 } \cdot g _ {11} \cdot x _ { 1 } Δw11=∂w11∂E=∂a3∂E⋅∂z3∂a3⋅∂a1∂z3⋅∂z1∂a1⋅∂w11∂z1 =g21⋅w21a1(1−a1)⋅x1 =g21⋅g11⋅x1
记 g 11 = w 21 a 1 ( 1 − a 1 ) g_{11} =w_{21} a _ { 1 } ( 1 - a _ {1 } ) g11=w21a1(1−a1)
Δ w 13 = ∂ E ∂ w 13 = ∂ E ∂ a 3 ⋅ ∂ a 3 ∂ z 3 ⋅ ∂ z 3 ∂ a 1 ⋅ ∂ a 1 ∂ z 1 ⋅ ∂ z 1 ∂ w 13 = g 21 ⋅ w 21 a 1 ( 1 − a 1 ) ⋅ x 2 = g 21 ⋅ g 11 ⋅ x 2 \Delta w_{13} = \frac{\partial E}{\partial w_{13}} =\frac{\partial E}{\partial a_{3}} \cdot \frac{\partial a_{3}}{\partial z_{3}} \cdot \frac{\partial z_{3}}{\partial a_{1}}\cdot \frac{\partial a_{1}}{\partial z_{1}}\cdot \frac{\partial z_{1}}{\partial w_{13}} \\\ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =g _ { 21 } \cdot w_{21} a _ { 1 } ( 1 - a _ {1 } ) \cdot x _ { 2 } \\ \ \\ \ \ \ \ \ \ = g _ { 2 1 } \cdot g _ {11} \cdot x _ { 2} Δw13=∂w13∂E=∂a3∂E⋅∂z3∂a3⋅∂a1∂z3⋅∂z1∂a1⋅∂w13∂z1 =g21⋅w21a1(1−a1)⋅x2 =g21⋅g11⋅x2
Δ b 1 = ∂ E ∂ b 1 = ∂ E ∂ a 3 ⋅ ∂ a 3 ∂ z 3 ⋅ ∂ z 3 ∂ a 1 ⋅ ∂ a 1 ∂ z 1 ⋅ ∂ z 1 ∂ b 1 = g 21 ⋅ g 11 \Delta b_{1} = \frac{\partial E}{\partial b_{1}} =\frac{\partial E}{\partial a_{3}} \cdot \frac{\partial a_{3}}{\partial z_{3}} \cdot \frac{\partial z_{3}}{\partial a_{1}}\cdot \frac{\partial a_{1}}{\partial z_{1}}\cdot \frac{\partial z_{1}}{\partial b_{1}} \\ \ \\ \ \ \ \ \ \ = g _ { 2 1 } \cdot g _ {11} Δb1=∂b1∂E=∂a3∂E⋅∂z3∂a3⋅∂a1∂z3⋅∂z1∂a1⋅∂b1∂z1 =g21⋅g11
Δ w 12 = ∂ E ∂ w 12 = ∂ E ∂ a 3 ⋅ ∂ a 3 ∂ z 3 ⋅ ∂ z 3 ∂ a 2 ⋅ ∂ a 2 ∂ z 2 ⋅ ∂ z 2 ∂ w 12 = g 21 ⋅ w 22 a 2 ( 1 − a 2 ) ⋅ x 1 = g 21 ⋅ g 12 ⋅ x 1 \Delta w_{12} = \frac{\partial E}{\partial w_{12}} =\frac{\partial E}{\partial a_{3}} \cdot \frac{\partial a_{3}}{\partial z_{3}} \cdot \frac{\partial z_{3}}{\partial a_{2}}\cdot \frac{\partial a_{2}}{\partial z_{2}}\cdot \frac{\partial z_{2}}{\partial w_{12}} \\\ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =g _ { 21 } \cdot w_{22} a _ { 2 } ( 1 - a _ {2 } ) \cdot x _ { 1 } \\ \ \\ \ \ \ \ \ \ = g _ { 2 1 } \cdot g _ {12} \cdot x _ { 1 } Δw12=∂w12∂E=∂a3∂E⋅∂z3∂a3⋅∂a2∂z3⋅∂z2∂a2⋅∂w12∂z2 =g21⋅w22a2(1−a2)⋅x1 =g21⋅g12⋅x1
记 g 12 = w 22 a 2 ( 1 − a 2 ) g_{12} =w_{22} a _ { 2 } ( 1 - a _ {2 } ) g12=w22a2(1−a2)
Δ w 14 = ∂ E ∂ w 14 = ∂ E ∂ a 3 ⋅ ∂ a 3 ∂ z 3 ⋅ ∂ z 3 ∂ a 2 ⋅ ∂ a 2 ∂ z 2 ⋅ ∂ z 2 ∂ w 14 = g 21 ⋅ w 22 a 2 ( 1 − a 2 ) ⋅ x 2 = g 21 ⋅ g 12 ⋅ x 2 \Delta w_{14} = \frac{\partial E}{\partial w_{14}} =\frac{\partial E}{\partial a_{3}} \cdot \frac{\partial a_{3}}{\partial z_{3}} \cdot \frac{\partial z_{3}}{\partial a_{2}}\cdot \frac{\partial a_{2}}{\partial z_{2}}\cdot \frac{\partial z_{2}}{\partial w_{14}} \\\ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =g _ { 21 } \cdot w_{22} a _ { 2 } ( 1 - a _ {2 } ) \cdot x _ { 2 } \\ \ \\ \ \ \ \ \ \ = g _ { 2 1 } \cdot g _ {12} \cdot x _ { 2 } Δw14=∂w14∂E=∂a3∂E⋅∂z3∂a3⋅∂a2∂z3⋅∂z2∂a2⋅∂w14∂z2 =g21⋅w22a2(1−a2)⋅x2 =g21⋅g12⋅x2
Δ b 2 = ∂ E ∂ w 12 = ∂ E ∂ a 3 ⋅ ∂ a 3 ∂ z 3 ⋅ ∂ z 3 ∂ a 2 ⋅ ∂ a 2 ∂ z 2 ⋅ ∂ z 2 ∂ b 2 = g 21 ⋅ g 12 \Delta b_{2} = \frac{\partial E}{\partial w_{12}} =\frac{\partial E}{\partial a_{3}} \cdot \frac{\partial a_{3}}{\partial z_{3}} \cdot \frac{\partial z_{3}}{\partial a_{2}}\cdot \frac{\partial a_{2}}{\partial z_{2}}\cdot \frac{\partial z_{2}}{\partial b_{2}} \\ \ \\ \ \ \ \ \ \ = g _ { 2 1 } \cdot g _ {12} Δb2=∂w12∂E=∂a3∂E⋅∂z3∂a3⋅∂a2∂z3⋅∂z2∂a2⋅∂b2∂z2 =g21⋅g12
累死了。。。。。够详细了吧,绝对能看懂。。。敲得咱脑瓜子疼,看懂了三连一下呗。。。。
矩阵版
有时间再写,晚安,希望可以梦到静静,疫情封城可真难熬啊,早点解封吧