单变量线性回归

假设某披萨店的披萨价格和披萨直径之间有下列数据关系：

根据上面的训练数据，我们能否推断(预测)出某个直径的披萨可能的售价呢？

例如：12英寸的披萨可能售卖多少钱？

因为披萨的价格是连续值，所有它是回归问题

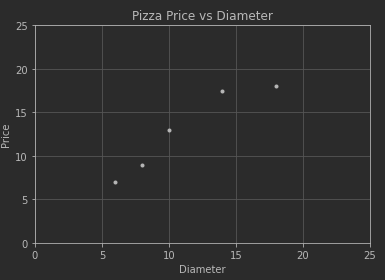
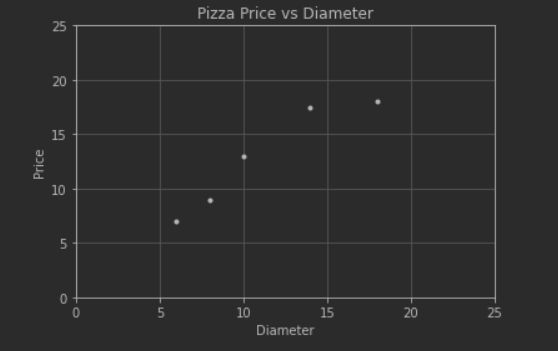
把直径看成自变量(以后也称特征值)，价格看成因变量，可以先通过作图看出二者的关系：

''' 查看样本数据 '''

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

def initPlot():
    plt.figure()
    plt.title('Pizza Price vs Diameter')
    plt.xlabel('Diameter')
    plt.ylabel('Price')
    plt.axis([0, 25, 0, 25])        # 设置x轴和y轴的值域均为0~25
    plt.grid(True)
    return plt

plt = initPlot()
xTrain = np.array([6,8,10,14,18])
yTrain = np.array([7,9,13,17.5,18])
plt.plot(xTrain, yTrain, 'k.')
plt.show()

可以看到：

价格y随着直径x的变化，大致呈现线性变化；

如果根据现有的训练数据能够拟合出一条直线，使之与这些训练数据的各点都比较接近，那么根据该直线，就可以计算出在任意直径披萨的价 格。

计算训练数据的线性相关性

# 计算训练数据的相关性：
import numpy as np
xTrain = np.array([6,8,10,14,18])
yTrain = np.array([7,9,13,17.5,18])
print(np.corrcoef(xTrain.T, yTrain.T))  # 计算训练数据的相关性  0.954

采用Python scikit-learn库中提供的sklearn.linear_model.LinearRegression对象来进行线性拟合 。
拟合出来的直线可以表示为：

表示Intercept Term，一般设置为1即可 。

表示影响计算结果的的第一个因素(或称特征，在本例中就是直径)。在单变量线性回归中，只有

表示截距，表示斜率。这两个参数都是需要通过拟合求出来的。

称为判别函数(Hypothesis Function)或判别式，也就是线性拟合的模型结果函数

解决思路:

构造残差函数（目标函数、成本函数）：

目标： 最小，求得：

• 步骤(引用scikit-learn库）

• 准备训练数据
  xTrain = np.array([6,8,10,14,18])[:, np.newaxis]
  yTrain = np.array([7,9,13,17.5,18])
  LinearRegression支持单变量和多变量回归。对于多变量回归，xTrain显然是矩阵形式。因此，即使只有一个变量，LinearRegression也要求输入的特征值以矩阵形式(列向量)存在。
  在使用LinearRegression时，不需要显式设置Intercept Item；它会自动扩展该列

• 创建模型对象
  model = LinearRegression()

• 执行拟合
  hypothesis = model.fit(xTrain, yTrain)
  判别函数(hypothesis)对象中包含了大量的属性和方法，可用于针对该模型的后续操作

• 获取判别函数的参数(截距和斜率)
  print(“theta0=”, hypothesis.intercept_)
  print(“theta1=”, hypothesis.coef_)

• 预测新的数据
  model.predict(12)
  model.predict([[0],[10],[14],[25]])
  将待预测的数据放置在一个矩阵(或列向量)中，可以批量预测多个数据

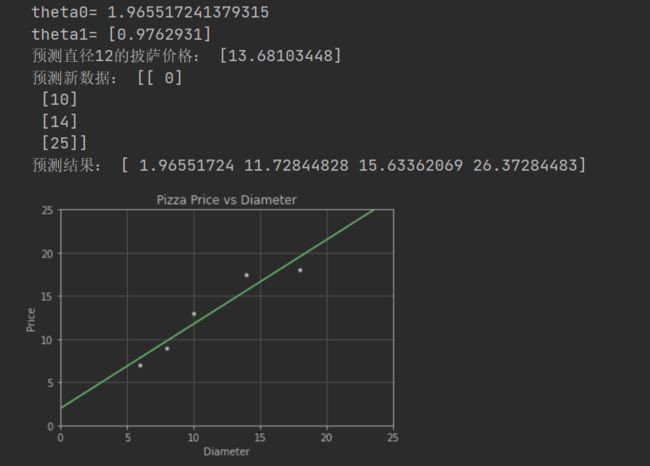
• 结果
  根据判别函数，绘制拟合直线，并同时显示训练数据点。
  拟合的直线较好的穿过训练数据，根据新拟合的直线，可以方便的求出各个直径下对应的价格(预测结果)。

''' 使用LinearRegression进行线性回归、预测，并作图显示结果 '''

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

xTrain = np.array([6,8,10,14,18])[:,np.newaxis]     # 应以矩阵形式表达(对于单变量，矩阵就是列向量形式)
yTrain = np.array([7,9,13,17.5,18])     # 为方便理解，也转换成列向量

model = LinearRegression()                  # 创建模型对象
hypothesis = model.fit(xTrain, yTrain)      # 根据训练数据拟合出直线(以得到假设函数)
print("theta0=", hypothesis.intercept_)     # 截距
print("theta1=", hypothesis.coef_)          # 斜率
        
print("预测直径12的披萨价格：", model.predict([[12]]))    # 预测直径为12的披萨价格
xNew = np.array([0, 10, 14, 25])[:,np.newaxis]            # 也可以批量预测多个直径，注意要以列向量形式表达
yNew = model.predict(xNew)
print("预测新数据：", xNew)
print("预测结果：",yNew)

def initPlot():
    plt.figure()
    plt.title('Pizza Price vs Diameter')
    plt.xlabel('Diameter')
    plt.ylabel('Price')
    plt.axis([0, 25, 0, 25])
    plt.grid(True)
    return plt

plt = initPlot()
plt.plot(xTrain, yTrain, 'k.')
plt.plot(xNew, yNew, 'g-')                  # 画出通过这些点的连续直线
plt.show()

xTrain = np.array([6,8,10,14,18])
print(xTrain)
print(xTrain.shape)
print(xTrain[:,np.newaxis])
print(xTrain[:,np.newaxis].shape)

模型评价

拟合出来的判别函数效果如何：对训练数据的贴合度如何？对新数据的预测准确度如何？

先给出下列定义：

• 残差(residuals)：判别函数计算结果与实际结果之间的差异，如下图中的红色线段部分。一般是计算残差平方和

• R方(r-squared)：又称确定系数(coefficient of determination)。在通过训练数据得出了判别函数后，对于新的数据，如何评估该假设函数的表现呢？可以使用与训练数据不同的另一组数据（称为检验/测试数据）来进行评估。R方就是用来进行评估的一种计算方法。在Pyhton的scikit-learn中，是这样定义R方的（针对给定的测试数据）：

（m倍的方差）
（残差平方和）

• 测试数据集中的数据组数

• 测试数据集中第组数据的值（实际价格）

• 测试数据集中的平均值

• 将代入到判别函数计算的结果，也就是根据模型算出的值（计算价格）

• 针对测试数据计算出来偏差平方和 即m倍的方差

• 针对测试数据计算出来的残差平方和

• 一般来说，R方越大(不会超过1)，说明模型效果越好。如果R方较小或为负，说明效果很差

• 在Python中如何对单变量线性回归模型的效果进行评估 * 手动计算 假设hpyTrain代表针对训练数据的预测值，hpyTest代表针对测试数据的预测值

• 训练数据残差平方和：ssResTrain = sum((hpyTrain - yTrain) ** 2)

• 测试数据残差平方和：ssResTest = sum((hpyTest - yTest) ** 2)

• 测试数据偏差平方和：ssTotTest = sum((yTest - np.mean(yTest)) ** 2) *

• R方：Rsquare = 1 - ssResTest / ssTotTest * R方越大拟合度越好

• 测试数据R方小于训练数据R方

• LinearRegression对象提供的方法 * 训练数据残差平方和：model._residues

• R方：model.score(xTest, yTest)

''' 计算模型的效果 '''

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

xTrain = np.array([6,8,10,14,18])[:,np.newaxis]         # 训练数据(直径)
yTrain = np.array([7,9,13,17.5,18])                     # 训练数据(价格)
xTest = np.array([8,9,11,16,12])[:,np.newaxis]          # 测试数据(直径)
yTest = np.array([11,8.5,15,18,11])                     # 测试数据(价格)

model = LinearRegression()
hypothesis = model.fit(xTrain, yTrain)
hpyTrain = model.predict(xTrain)
hpyTest = model.predict(xTest)                          # 针对测试数据进行预测

ssResTrain = sum((hpyTrain - yTrain)**2)                # 手动计算训练数据集残差
print(ssResTrain)                                       # 8.7478
print(model._residues)                                  # Python计算的训练数据集残差

ssResTest = sum((hpyTest - yTest)**2)                   # 手动计算测试数据集残差
ssTotTest = sum((yTest - np.mean(yTest))**2)            # 手动计算测试数据集y值偏差平方和
Rsquare = 1 - ssResTest / ssTotTest                     # 手动计算R方
print(Rsquare)                                          # 0.662
print('testR2',model.score(xTest, yTest))               # Python计算的测试数据集的R方
print('trainR2',model.score(xTrain, yTrain))            # Python计算的测试数据集的R方       

# corrcoef函数是在各行元素之间计算相关性，所以x和y都应是行向量
print(np.corrcoef(xTrain.T, yTrain.T))            # 计算训练数据的相关性：0.954
print(np.corrcoef(xTest.T, yTest.T))              # 计算测试数据的相关性：0.816

def initPlot():
    plt.figure()
    plt.title('Pizza Price vs Diameter')
    plt.xlabel('Diameter')
    plt.ylabel('Price')
    plt.axis([0, 25, 0, 25])
    plt.grid(True)
    return plt

plt = initPlot()
plt.plot(xTrain, yTrain, 'r.')          # 训练点数据(红色)
plt.plot(xTest, yTest, 'b.')            # 测试点数据(蓝色)
plt.plot(xTrain, hpyTrain, 'g-')        # 假设函数直线(绿色)
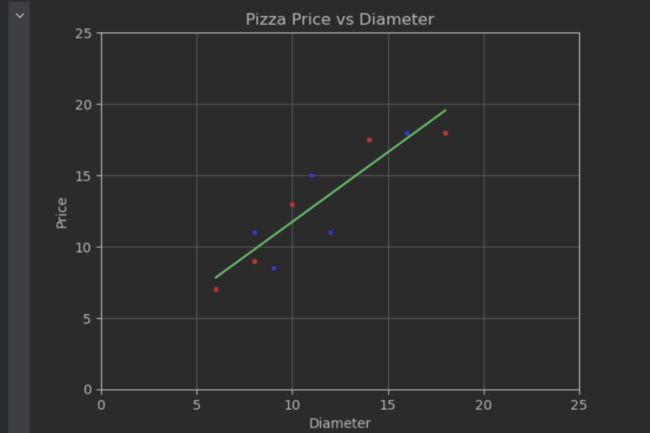
plt.show()

查看上述拟合效果：

• 红色为训练数据点，蓝色为测试数据点，绿色为判别函数(拟合直线)

• 计算出测试集的R方为0.662，效果一般

• 计算出训练数据的相关性为0.954，测试数据的相关性为0.816。可以发现，根据数据集的不同，直径与价格之间的相关性波动较大。这也能解释为何针对测试数据的R方事实上不够理想

• 竞赛经常以残差平方和为评判标准