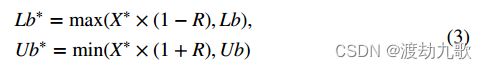蜣螂优化(DBO)算法附MATLAB代码

目录

一、蜣螂优化(DBO)算法灵感来源

二、蜣螂优化(DBO)算法设计

三、蜣螂优化(DBO)算法MATLAB部分代码

四、运行结果

       蜣螂优化(Dung Beetle Optimizer, DBO)算法是2022年11月27日提出的，大家可以算算到今天才提出多久。它是由东华大学的沈波教授团队提出的一种全新的群智能优化算法。或许大家对这个团队不是很了解，但相信大家对麻雀搜索算法一定不陌生，著名的SSA就是由这个团队提出。基于屎壳郎的滚球、跳舞、觅食、偷窃和繁殖行为，提出了一种基于种群的屎壳郎优化算法(DBO)。新提出的DBO算法兼顾了全局探索和局部开发，具有收敛速度快、解精度高的特点。

       在本文中，详细讨论了一种新的基于si的优化技术——DBO算法，包括以下两个方面:灵感和数学模型。

一、蜣螂优化(DBO)算法灵感来源

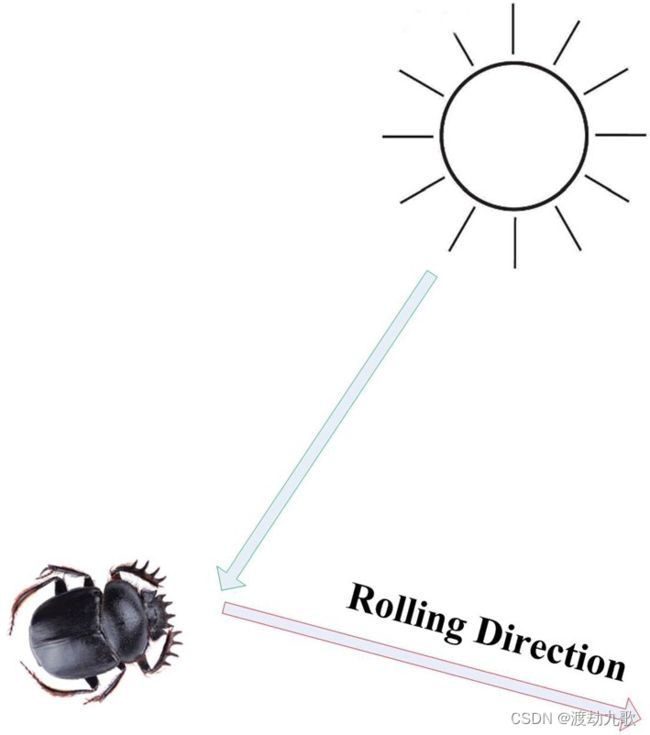
       众所周知，屎壳郎是自然界中一种常见的昆虫，以动物的粪便为食。请注意，蜣螂在世界上大部分地区都有发现，它们在自然界中扮演着分解者的角色，这意味着它们在生态系统中至关重要。研究表明，蜣螂有一个有趣的习惯，就是把粪便揉成一个球，然后把它滚出去，如图1所示。值得一提的是，屎壳郎的目的是为了尽可能快速有效地移动它们的粪球，这可以防止它们与其他蜣螂竞争。

图1

       如图1所示，一只屎壳虫正在向后滚一个比自己还大的粪球。另一方面，屎壳郎有一种奇妙的行为，它可以利用天体的线索(尤其是太阳、月亮和偏振光)来导航，使粪球沿直线滚动。然而，如果根本没有光源(即完全黑暗)，蜣螂的路径就不再是笔直的，而是弯曲的，有时甚至有点圆。注意，许多自然因素(如风和不平整的地面)会导致蜣螂偏离原来的方向。此外，屎壳郎在滚动的过程中很可能会遇到障碍物，无法前进。对此，蜣螂通常会爬到粪球上跳舞(包括一系列的旋转和停顿)，这决定了它们的运动方向.

        从蜣螂的生活方式中观察到的另一个有趣的行为是，获得的粪球有以下两个主要目的:1)一些粪球用来产卵和抚养下一代，2)其余的用作食物。具体来说，蜣螂把粪球埋起来，雌性蜣螂在这些粪球里产卵。需要注意的是，粪球不仅是幼虫发育的场所，也为幼虫提供了生命所必需的食物。因此，粪球对屎壳郎的生存起着不可替代的作用。

        一种新的SI优化算法——DBO技术，主要是受到蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为的启发。

二、蜣螂优化(DBO)算法设计

      根据上面的讨论，我们知道蜣螂在滚动过程中需要通过天体线索来导航，以保持粪球在一条直线上滚动。为了模拟滚球行为，蜣螂需要在整个搜索空间中沿着给定的方向移动。屎壳郎的飞行轨迹如图2所示。在这张图中，我们可以看到蜣螂利用太阳来导航，其中红色箭头表示滚动方向。在本文中，我们假设光源的强度也会影响蜣螂的路径。在滚动过程中，滚球蜣螂的位置被更新，可以表示为

式中，表示当前迭代次数,表示第i只蜣螂在第n次迭代时的位置信息，k∈(0,0.2]表示一个常数，该常数表示缺陷系数，b表示一个属于(0,1)的常数,为自然系数，赋值为-1或1,表示全局最差位置，Δx用于模拟光强的变化。

图2

在(1)中，两个参数(k和b)选择合适的值至关重要。请注意훼意味着许多自然因素(如风和不平整的地面)会使蜣螂偏离原来的方向。其中= 1表示不偏离，=−1表示偏离原方向。为了模拟现实世界的复杂环境，本文采用概率法将设为1或-1(见算法1)。同样，Δx值越高，表示光源越弱。另外，k和b分别设为0.1和0.3。Δx可以促进滚球蜣螂具有以下两个优点:1)在优化过程中尽可能彻底地探索整个问题空间;2)追求更强的搜索性能，减少陷入局部最优的可能性。因此，更适合控制Δx的值来扩展搜索范围。 

         当屎壳郎遇到障碍物无法前进时，它需要通过跳舞来重新定位自己，目的是获得一条新的路线。值得注意的是，舞蹈行为在滚球的蜣螂中起着重要作用。图2屎壳郎飞行轨迹的概念模型。

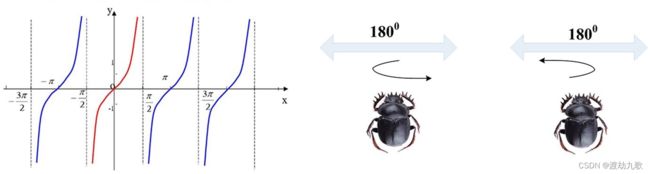图3

为了模拟舞蹈行为，我们使用正切函数来获得新的滚动方向。需要说明的是，我们只需要考虑在区间上定义的切函数的值，如图3所示。一旦蜣螂成功地确定了一个新的方向，它应该继续向后滚动球。因此，将滚球蜣螂的位置更新定义如下: 

式中为属于的倾斜角。 

       式(2)中，∣xi (t)−xi (t−1)∣为第i只屎壳虫在第n次迭代时的位置与第t−1次迭代时的位置之差。因此，滚球蜣螂的位置更新与当前和历史信息密切相关，请注意，如果等于0、/2或，则蜣螂的位置不会更新(参见算法2)。

       在自然界中，蜣螂会把粪球滚到安全的地方并藏起来(见图4)。为了给它们的后代提供一个安全的环境，选择合适的产卵地点对蜣螂来说至关重要。受上述讨论的启发，提出了一种边界选择策略来模拟雌性蜣螂产卵的区域，其定义为

 式中，表示当前局部最优位置，Lb∗和Ub∗分别表示产卵区域的下界和上界，和表示最大迭代次数，Lb和Ub分别表示优化问题的下界和上界。

       如图5所示，当前局部最佳位置用一个大的棕色圆圈表示，而周围的小黑色圆圈表示育雏球。请注意，每个育仔球都包含一枚屎壳虫卵(见图4)。此外，红色小圆圈代表边界的上下限。一旦确定了产卵区域，雌性蜣螂就会选择这个区域的卵球产卵。需要说明的是，对于DBO算法，每只雌性蜣螂在每次迭代中只产生一个卵。此外，由(3)可以清楚地看出，产卵区的边界范围是动态变化的，这主要是由R值决定的。因此，孵化球的位置在迭代过程中也是动态的，定义为

式中，为第i个育雏球在第n次迭代时的位置信息，和表示大小为1 × D的两个独立随机向量，D表示优化问题的维数。注意孵蛋球的位置被严格限制在一定范围内，即产卵区域(见算法3)。

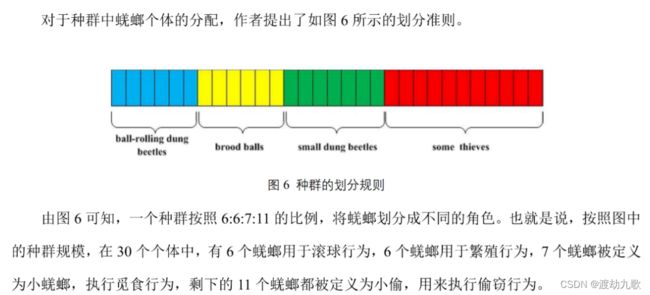
一些已经长大成人的屎壳郎会从地下钻出来寻找食物(见图6)。在本文中，我们称它们为小屎壳郎。此外，我们还需要建立最佳觅食区域来指导甲虫的觅食，并进行模拟这些屎壳郎在自然界的觅食过程。其中，最优觅食区域的边界定义为:

式中,表示全局最佳位置，Lb和Ub分别表示最优觅食区域的下界和上界，其他参数定义如(3)所示。因此，小屎壳郎的位置更新如下:

式中,表示第i只小蜣螂在第n次迭代时的位置信息，表示服从正态分布的随机数，表示属于(0,1)的随机向量。

       另一方面，有些屎壳郎，被称为小偷，会从其他屎壳郎身上偷粪球(见图7)。需要指出的是，这是自然界中很常见的现象。由(5)可知，是最优食物源。因此，我们可以假设周围的表示争夺食物的最佳地点。在迭代过程中，小偷的位置信息更新，可以描述为:

 式中表示第i个贼在第n次迭代时的位置信息，g是大小为1 × D的随机向量，服从正态分布，S表示常数。

图5

图6

图7

       由于DBO算法将种群中的蜣螂划分成了四种不同的角色，因此它的计算流程会相对复杂一些，需要执行滚球、繁殖、觅食和偷窃四种算子。这里我用伪代码给出了它的计算流程： 

 三、蜣螂优化(DBO)算法MATLAB部分代码

function [fMin , bestX, Convergence_curve ] = DBO(pop, M,c,d,dim,fobj)       
P_percent = 0.2;                  % The population size of producers accounts for "P_percent" percent of the total population size       
pNum = round( pop * P_percent );  % The population size of the producers   
lb= c.*ones( 1,dim );    
ub= d.*ones( 1,dim );  
%Initialization
for i = 1 : pop  
    x( i, : ) = lb + (ub - lb) .* rand( 1, dim ); 
    fit( i )  = fobj( x( i, : )) ;                       
end
pFit = fit;                       
pX=x; 
XX=pX;    
[fMin,bestI] = min(fit);      % fMin denotes the global optimum fitness value
bestX = x(bestI,:);           % bestX denotes the global optimum position corresponding to fMin
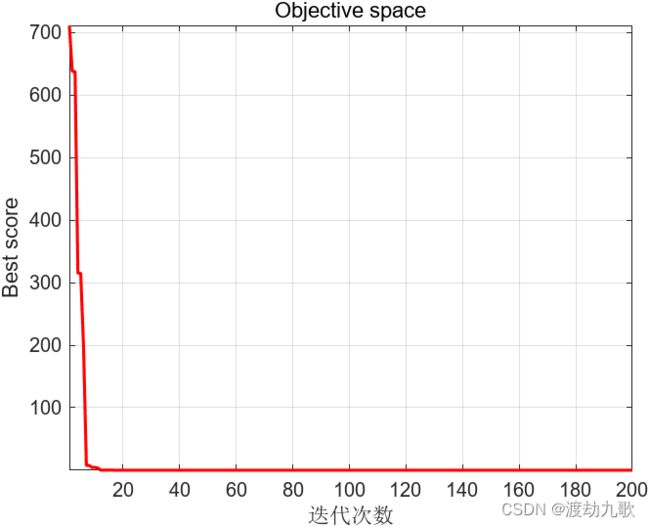
% Start updating the solutions.

 四、运行结果

The best solution obtained by DBO is : 3.2411e-25 -3.4589e-25 1.3799e-24 1.3902e-24 4.566e-26 -2.7352e-25 4.8812e-25 -1.8461e-24 -1.545e-24 -5.3451e-28
The best optimal value of the objective funciton found by DBO is : 1.0172e-47

    可以看出新提出的DBO算法兼顾了全局探索和局部开发，具有收敛速度快、解精度高的特点。