VAE, the principle and the code

VAE

keywords encoder, decoder

Concepts

Variational autoencoder(VAE) is a latent model $p(x,z|\theta )$.​

probabilistic encoder-decoder:

• probabilistic decoder/likelihood/generating proba: $p(x|z,\theta )$​, the distribution of the decoded variable given the encoded one,

• probabilistic encoder/posterior/predicting(discriminant, respondant) proba/encoding: $p(z|x,\theta )$​, the distribution of the encoded variable given the decoded one.

graph: $z\to x(\leftarrow \theta )$​​​​​

Task: to find $q(z)\approx p(z|x)$​​​​​​​​​​, or denoted as $q(z|x)$​​ to emphsize the dependence on $x$. (variational inference)

loss: $D_{KL}(q(z)\Vert p(z|x))$​

likelihood: $l(\theta )={\sum }_x\ln {\int }_{z}p(x|z,\theta )p(z|\theta )dz$

Variational Lower Bound/Evidence Lower Bound(ELBO)
$$\begin{gathered} L_x:=E_{z\sim q}(\log p(x,z)-\log q(z)) \\ =Q(p,q)+H(q)(=F(p,q)) \end{gathered}$$
where $q$ alwayes depends on $x$​.

Remark $L_x$ is also called free energy.

ELBO = expected likelihood + entropy

(EM algo. / MM algo.)

Facts

Identity

variational inequality
$$\log p(x)=D_{KL}(q(z)\Vert p(z|x))+L_x\ge L_x$$

remark likelihood = divergence + ELBO(free energy)

$$L_x=E_{z\sim q}(\log p(x|z))-D_{KL}(q(z)\Vert p_Z(z)),$$

ELBO = Reconstruction loss + Regularization term

Reconstruction loss: $-E_{z\sim q}(\log p(x|z))$​​

Regularization term: $D_{KL}(q\Vert p_Z)$

For samples $D$,
$$L_D=\sum _{x\in D}{E}_{z\sim q}\log p(x|z)-D_{KL}(q\Vert p_Z)$$

remark For fixed $p$​, ${\min }_{p,q}{D}_{KL}⟺{\max }_{p,q}{L}_x$​​​​.

diff. between EM and VAE

• EM algorithm: solve $\max L_x$ by coordinate ascent
• VAE: by SGD

Parameter form
$$\begin{gathered} L_D(\theta ,\varphi )=\sum _{x\in D}(E_{z\sim q_{x,\varphi }}\log p(x|z,\theta )-D_{KL}(q(z|x,\varphi )\Vert p(z|\theta ))) \\ =\sum _{x\in D}(E_{z\sim q_{x,\varphi }}\log p(x|z,\theta )-D_{KL}(q(z|x,\varphi )\Vert p(z)))(if\theta \to x\leftarrow z) \end{gathered}$$
where variational parameters:$\varphi$, generative parameters: $\theta$​.

Assumptions

Gaussian assumption: $p(z),p(x|z)$: Gaussian distr.
$$\begin{gathered} Z\sim N(0,1), \\ X|Z=z\sim N(f(z),c),f\in F,c>0. \end{gathered}$$
It is intractable to compute $p(z|x)$ by Bayesian formula.

variational inference(VI)

VI is a technique to approximate complex distributions

Continue from (4)

We are going to approximate $p(z|x)$​ by a Gaussian distribution $q_x(z)$​​ whose mean and covariance are defined by two functions, $g$​ and $h$​, of the parameter $x$​.
$$q(Z|x)\sim N(g(x),h(x)),g\in G,h\in H,$$
where variational parameter $\varphi =(g,h)\in G\times H$​.

Fixed $f$ (hence $\log p(x)$ is a constant), solve the following optimialization problem,

$$\begin{gathered} \max L_x⟺\underset{g,h}{\min }{D}_{KL}(q_x(z)\Vert p(z|x)) \\ \simeq \underset{g,h}{\min }-E\log p(x|z)+D_{KL}(q_x\Vert p_Z) \\ =\underset{g,h}{\min }\frac{1}{2c}E\Vert x-f(z){\Vert }^2+D_{KL}(q_x\Vert p_Z). \end{gathered}$$

Then find optimal $f$​​​​,
$$\underset{f}{\max }{E}_{z\sim N(g(x),h(x))}\log p(x|z)=\underset{f}{\min }{E}_z\Vert x-f(z){\Vert }^2$$

===>
$$=\frac{1}{2c}\underset{f,g,h}{\min }{E}_z\Vert x-f(z){\Vert }^2+D_{KL}(q_x\Vert p_Z).$$

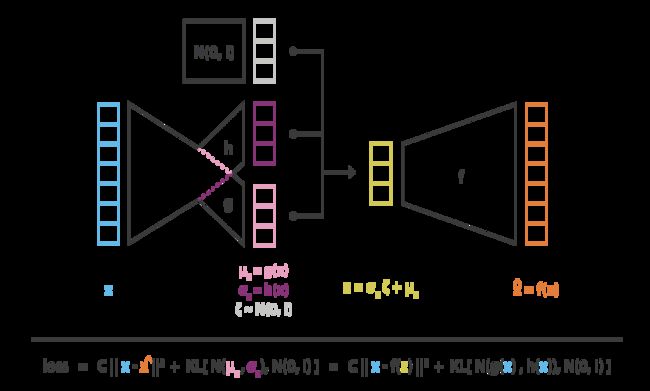
variational autoencoder(AVE) architecture

Based on Gaussian assumption.

architecture

encoder: $x\to z=g(x)+h(x)\zeta \sim N(g(x),h(x))$​​​​​​​​ and $\zeta \sim N(0,1)$​​​​​​ (reparameterization), as an approximation of $p(z|x)$​​

decoder: $z\to x\sim N(f(z),c)$​​

reparametrisation trick
$$L(x)=C{E}_z\Vert x-f(z){\Vert }^2+D_{KL}(N(g(x),h(x))\Vert N(0,1))$$

where $D_{KL}$​ of the diagonal normal distr. and standard normal distr. is $D_{KL}(DN,SN):=\frac{1}{2}{\sum }_{i=1}^k({\sigma }_i^2+{\mu }_i^2-1-\ln {\sigma }_i^2)$​​​​​​​, where ${\mu }_i=g_i(x),{\sigma }_i^2=h_i(x)$.

see Wiki of KL divergence.

Bayes-by-BP

Algo

1. initalize $\varphi \leftarrow {\varphi }_0$
2. loop from i=0 to N
   1. $z\sim q(z|x,\varphi )$;
   2. $\theta$​ maximizes $\log p(x|z,\theta )$;
   3. calculate ELBO $L(\theta ,\varphi )$;
   4. update $\varphi$ by GD;

General form of Algorithm

opt $F(\theta )=E_{z\sim q_{\theta }}f(\theta ,z)$​​​​​​:

1. guess $\theta$, generate $z\sim q_{\theta }$;
2. Do GD for $f(\theta ,z)$​​​​ to update $\theta$​​;

PCA/SVD as a VAE

General form encoder-decoder model
$$\underset{d,e}{\min }|x-d(e(x))|$$

SVD, dim of data space = p, laten space = q
$$\begin{gathered} \underset{V}{\min }|X-X{V}_q{V}_q^{\prime }| \\ V:O(p) \end{gathered}$$

xi ~ N(0,1)
   \
D -- > Z --> X = ZV'

where $Z\sim N(0,D),X=Z{V}^{\prime }$​​​.

stat. model of encoder-decoder

• encoder: $p(x|z)$
• decoder: $p(z|x)$

as the conditional proba. of $p(x,z)$

generating rask: $z\sim N(0,1)\Rightarrow x\sim p(x|z)$

Basic Model

graph: c -> z -> x (<-theta), where $c$: context.

Likelihood: $p(D|\theta )={\prod }_{x\in D}\int p(x|z,\theta )p(z|c,\theta )dz$​​

variational lower bound:
$$L_D=E_{c\sim q_D}(L_{D|c})-D_{KL}(q_D\Vert p_c)$$

Full Model

graph: c -> z1,...,zT -> x (<-theta), where $c$: context.

References

understanding-variational-autoencoders

Ming Ding. The road from MLE to EM to VAE: A brief tutorial,2022.
H Edwards, A. Storkey. Towards a neural statistician,2017.

Codes

code on line:
VAE-keras

my code:

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

"""
VAE
"""

import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers


class Sampling(layers.Layer):
    """Sampling Layer for reparameterization
    Uses (z_mean, z_log_var) to sample z, the vector encoding a digit.
    """

    def call(self, inputs):
        z_mean, z_log_var = inputs
        batch, dim = tf.shape(z_mean)[0], tf.shape(z_mean)[1]
        epsilon = tf.keras.backend.random_normal(shape=(batch, dim))
        return z_mean + tf.exp(0.5 * z_log_var) * epsilon


class VAE(keras.Model):
    # architechture of VAE
    def __init__(self, latent_dim, **kwargs):
        super().__init__(**kwargs)
        self.latent_dim = latent_dim
        self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
        self.reconstruction_loss_tracker = keras.metrics.Mean(name="reconstruction_loss")
        self.kl_loss_tracker = keras.metrics.Mean(name="kl_loss")

    @property
    def metrics(self):
        return [
            self.total_loss_tracker,
            self.reconstruction_loss_tracker,
            self.kl_loss_tracker,
        ]

    def train_step(self, data):
        with tf.GradientTape() as tape:
            z_mean, z_log_var, z = self.encoder(data)
            reconstruction = self.decoder(z)
            reconstruction_loss = tf.reduce_mean(
                tf.reduce_sum(
                    keras.losses.binary_crossentropy(data, reconstruction), axis=(1, 2)
                )
            )  # Hb(x_i, f(z_i)) z_i ~ N(g(x_i),h(x_i))
            kl_loss = 0.5 * tf.reduce_sum(tf.square(z_mean) + tf.exp(z_log_var) - 1 - z_log_var, axis=1)
            kl_loss = tf.reduce_mean(kl_loss)    # KL-div of N and SN
            total_loss = reconstruction_loss + kl_loss
        grads = tape.gradient(total_loss, self.trainable_weights)
        self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
        self.total_loss_tracker.update_state(total_loss)
        self.reconstruction_loss_tracker.update_state(reconstruction_loss)
        self.kl_loss_tracker.update_state(kl_loss)

        return {
            "loss": self.total_loss_tracker.result(),
            "reconstruction_loss": self.reconstruction_loss_tracker.result(),
            "kl_loss": self.kl_loss_tracker.result()}

    @classmethod
    def make_from_data(cls, X, latent_dim, *args, **kwargs):
        shape = X.shape[1:3]
        return cls.make(shape, latent_dim, *args, **kwargs)

    @classmethod
    def make(cls, shape, latent_dim, *args, **kwargs):
        assert len(shape)>=2, "Sorry, this VAE works only for images; the ndim of each sample>=2!"
        model = cls(latent_dim, *args, **kwargs)
        model.encoder = cls.make_encoder(shape, latent_dim)
        model.decoder = cls.make_decoder(shape, latent_dim)
        model.compile(optimizer=keras.optimizers.Adam())
        return model

    @classmethod
    def make_encoder(cls, shape, latent_dim):
        # shape: the shape of input data
        if len(shape)==2:
            height, width = shape
            n_channels = 1
        elif len(shape)==3:
            height, width, n_channels = shape

        encoder_inputs = layers.Input(shape=(height, width, n_channels))
        x = layers.Conv2D(32, 3, activation="relu", strides=2, padding="same")(encoder_inputs)
        x = layers.Conv2D(64, 3, activation="relu", strides=2, padding="same")(x)
        x = layers.Flatten()(x)
        x = layers.Dense(16, activation="relu")(x)
        z_mean = layers.Dense(latent_dim, name="z_mean")(x)       # g(x)
        z_log_var = layers.Dense(latent_dim, name="z_log_var")(x) # h(x)
        z = Sampling()([z_mean, z_log_var])                       # z ~ N(g(x),h(x))
        return keras.Model(encoder_inputs, [z_mean, z_log_var, z], name="encoder")

    @classmethod
    def make_decoder(cls, shape, latent_dim):
        # x = f(z), shape: the shape of the output of the decoder
        if len(shape)==2:
            height, width = shape
            n_channels = 1
        elif len(shape)==3:
            height, width, n_channels = shape
        small_height, small_width = height // 4, width // 4
        decoder = keras.Sequential(name="decoder")     # f(z)
        latent_inputs = keras.Input(shape=(latent_dim,))
        decoder.add(latent_inputs)
        decoder.add(layers.Dense(small_height * small_width * 64, activation="relu"))
        decoder.add(layers.Reshape((small_height, small_width, 64)))
        decoder.add(layers.Conv2DTranspose(64, 3, activation="relu", strides=2, padding="same"))
        decoder.add(layers.Conv2DTranspose(32, 3, activation="relu", strides=2, padding="same"))
        decoder.add(layers.Conv2DTranspose(1, 3, activation="sigmoid", padding="same"))
        return decoder

    def trainsform(self, X):
        M, _, _ = self.encoder(X)
        return M

    def inverse_trainsform(self, Z):
        return self.decoder.predict(Z)


def plot_latent_space(vae, n=11, *args, **kwargs):

    import itertools
    import matplotlib.pyplot as plt

    # display a n*n 2D manifold of digits
    scale = 1.0

    # linearly spaced coordinates corresponding to the 2D plot
    # of digit classes in the latent space
    grid_x = np.linspace(-scale, scale, n)
    grid_y = np.linspace(-scale, scale, n)[::-1]
    z_sample = np.hstack((list(itertools.product(grid_y, grid_x)), np.random.normal(size=(n**2, vae.latent_dim-2))))
    x_decoded = vae.inverse_trainsform(z_sample)

    figure = np.block([[x_decoded[i*n+j].reshape((width, height)) for j in range(n)] for i in range(n)])

    plt.figure(*args, **kwargs)
    start_range_x, start_range_y = width // 2, height // 2
    end_range_x = n * width + start_range_x
    end_range_y = n * height + start_range_y
    pixel_range_x = np.arange(start_range_x, end_range_x, width)
    pixel_range_y = np.arange(start_range_y, end_range_y, height)
    sample_range_x = np.round(grid_x, 1)
    sample_range_y = np.round(grid_y, 1)
    plt.xticks(pixel_range_x, sample_range_x)
    plt.yticks(pixel_range_y, sample_range_y)
    plt.xlabel("$z_0$")
    plt.ylabel("$z_1$")
    plt.imshow(figure, cmap="Greys_r")
    plt.show()

if __name__ == '__main__':
    
    # from get_hanzi import X_train
    # input your data here, images in size of 4m X 4n

    X_train /= 255
    X_train = X_train>0.5  # binarize

    X_train = np.expand_dims(X_train, -1).astype("float32")
    vae = VAE.make_from_data(X_train, latent_dim=15)
    vae.fit(X_train, epochs=200, batch_size=16, verbose=False)
    plot_latent_space(vae)