2023/6/8总结
MySQL必知必会
commit 和 rollback 的差异是commit会提交,而rollback不会,就好像是撤回。
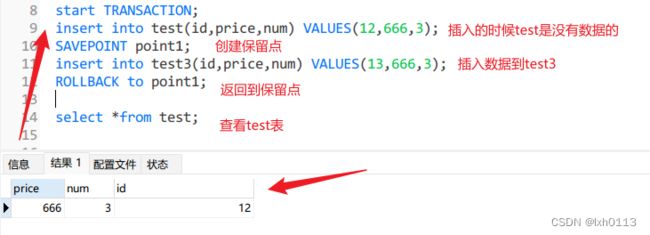
使用保留点:
简单的rollback和commit语句就可以写入或者撤销整个事务处理,但是,只是对简单的事务处理才能这样做,更简单的事务处理可能需要部分提交或回退。
为了支持回退部分事务处理,必须能在事务处理块中合适的位置放置占位符。这样,如果需要回退,可以退回到某个占位符。
这些占位符称为保留点,为了创建占位符,可以使用:
语法:
保留点在事务处理完成,执行一条rollback或者commit后自动释放,也可以用release savepoint明确地释放保留点。
如果需要回退:
回退语法:rollback to 保留点名称
更改默认的提交行为:
MySQL默认行为是自动提交所有更改,如果想要MySQL不自动提交更改,需要使用以下语句。
设置回去是:
字符集和校对顺序:
MySQL需要适应不同的字符集(不同的字母和字符),适应不同的排序和检索数据的方法。
- 字符集为字母和符号的集合
- 编码为某个字符集成员的内部表示
- 校对为规定字符如何比较的指令。
校对的重要性:在数据的排序时,如果想要拿到自己想要的正确顺序,就需要校对
-
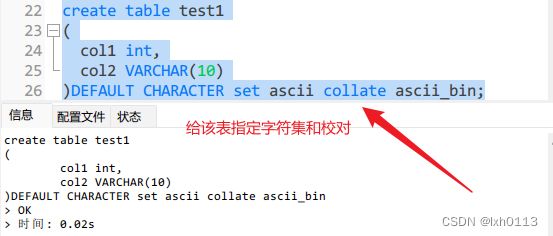
给表指定字符集和校对
-
对列进行指定字符集和校对
如果需要用与创建表时不同的校对顺序排序特定的select语句:
安全管理:
访问控制:
MySQL服务器的安全基础是,用户应该对他们需要的数据具有适当的访问权。
使用访问权的情况:
- 多数用户只需要对表进行读和写,但是少数用户需要能创建表和删除表。
- 某些用户需要读表,但是不需要更新表
- 允许用户添加数据,但是不允许删除数据
- 一些用户需要处理用户账号的权限,但是多数用户不需要。
- 让用户通过存储过程访问数据,但是不能直接访问数据
- 根据用户登录的地点限制对某些功能的访问。
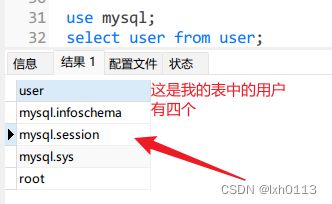
MySQL的数据库的user表里面包含所有的用户账号。
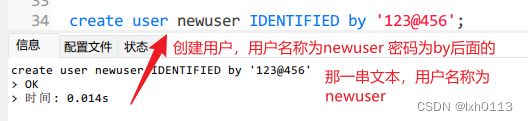
创建用户账号:
identified by 指定的口令为纯文本,MySQL将保存到user表之前对其进行加密,为了作为散列值指定口令,使用identified by password。
使用grant或者insert grant语句也可以创建用户账户,但是一般来说creat user是最清楚和最简单的句子。此外也可以通过插入行列到user表来增加用户,但是为了安全起见,不建议这样做。MySQL用来存储用户账号信息的表极为重要,对它们的任何毁坏都可能严重地伤害到MySQL服务器。
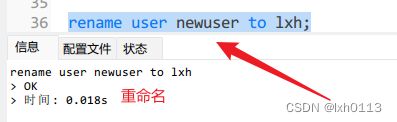
重命名用户账户
rename user只在mysql5之后的版本支持。
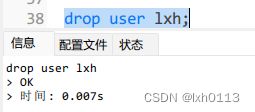
删除用户账号:
设置访问权限:
创建用户账号后,必须接着分配访问权限。新创建的用户账号没有访问权限。能登录MySQL,不能看到数据,不能执行任何数据库操作。
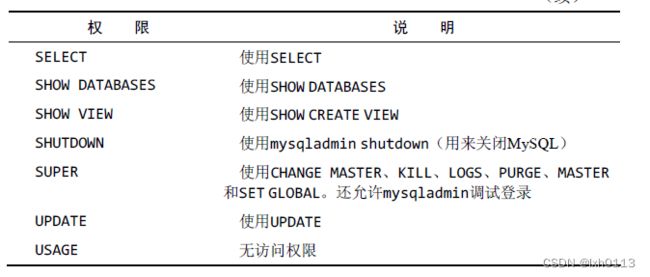
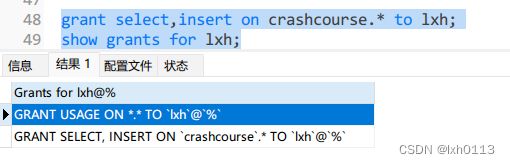
这是查看用户账号的权限:(目前还是看不懂)
设置权限,使用grant语句,需要给出以下信息:
- 要授予的权限
- 被授予访问权限的数据库或者表
- 用户名
每个grant添加(或更新)用户的一个权限,MySQL读取所有的授权,并根据它们确定权限。
grant 的反向操作是revoke 用来撤销特定的权限。
是revoke而不是remove
grant和revoke可以在几个层次上控制访问权限:
- 整个服务器:grant all 和 revoke all
- 整个数据库:on database.*
- 特定的表,使用on database.table
- 特定的列
- 特定的存储过程
- 具体的表:
未来的授权:在使用grant 和 revoke ,用户账号必须存在, 但是所涉及的对象没有这个要求,这允许管理员在创建数据库和表之前设计和实现安全措施。但是这样做的副作用是,当某个数据库或者表被删除时(drop语句),相关的权限依然起作用。
简化授权:
可以通过累出各权限,将多条grant语句串在一起:
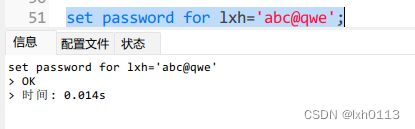
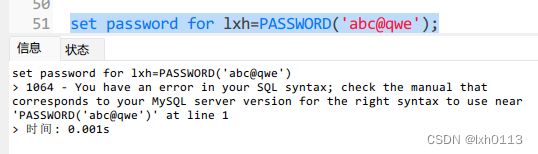
更改用户口令(密码)
书上说应该这样写:(但是一直没成功)
在不指定用户名时,set password更新当前登录用户的口令。
数据库维护:
备份数据:
解决方案:
- 使用命令行实用程序MySQLdump转储所有数据库内容到某个外部文件,在进行常规备份钱这个实用程序应该正确地备份转储文件。
- 可用命令行实用程序MySQLhotcopy从一个数据库复制所有数据(但是不是所有数据库引擎都支持这个实用程序)。
- 可以使用MySQL的backup table或者select into outfile 转储所有数据到某个外部文件,这俩条语句都接受将要创建的系统文件名,此系统文件必须不存在,否则会出错。数据可以用restore table来复原。
进行数据库维护:
检查表键是否正确
check table用来针对许多问题对表进行检查。在MyISAM表上还对索引进行检查。check table支持一系列的用于MyISAM表的方式。changed检查自最后一次检查以来改动过的表,extended执行最彻底的检查,fast只检查未正常关闭的表,medium检查所有被删除的链接并进行键检验,quick只进行快速扫描。
如果MyISAM表访问产生不正确和不一致的结果,可能需要用repair table来修复相应的表。但是这条语句不应该多次使用,经常使用可能会有更大的问题要解决。
如果从一个表中删除大量数据,应该使用optimize table来收回所用的空间,从而优化表的性能。
改善性能:
- 查看当前设置,可以使用show variables 和show status
- MySQL是一个多用户多线程的DBMS,它经常同时执行多个任务,如果这些任务中的某一个执行缓慢,则所有请求都会执行缓慢。如果遇到这样的情况,可以使用show processlist显示所有活动进程(以及它们的线程ID和执行时间),可以用kill命令终结某个特定的进程(但是需要作为管理员登录)
- 使用explain语句让MySQL解释它将如何执行一条select语句

- 一般来说,存储过程执行得比一天一天地执行其中各条MySQL语句快。
- 在导入数据时,应该关闭自动提交,如果要删除索引(包括fulltext索引),应该在导入完成后再重建它们。
- 使用union语句比一系列复杂得or条件要好的多。
- 索引改善数据检索得性能,但是损害数据插入、删除和更新的性能。如果你的表只是要收集数据,则在有必要之前不要索引它们。
- like很慢,最好使用fulltext而不是like
题解:
第三次题组 [Cloned] - Virtual Judge (vjudge.net)
1.这道题其实就是需要求出 a^c1+c2*b 是否存在这个c2让剩下的数字整除a
2.但是a=1的时候需要特判一下
#include
int slove(long long n,long long a,long long b)
{
if(a==1)
{
if((n-1)%b==0) return 1;
else return 0;
}
long long num=1;
int flag=0;
while(num<=n)
{
if((n-num)%b==0)
{
flag=1;break;
}
num*=a;
}
return flag;
}
int main()
{
//倍数、加起来相等
long long t,i,j,n,a,b;
scanf("%lld",&t);
for(i=0;i 第三次题组 [Cloned] - Virtual Judge (vjudge.net)
1.这一题是算出区间,每次贪心取一个区间保留下来,然后对比顾客的适宜温度。
2,最高值的区间需要取到当前和之前的最小,后面好变化一点。最低值相反。
#include
#define Maxsize 510
int t[Maxsize],l[Maxsize],h[Maxsize];
int q,n,m;
int MAX(int a,int b)
{
if(a>b) return a;
return b;
}
int MIN(int a,int b)
{
if(amaxt||h[i] 第三次题组 [Cloned] - Virtual Judge (vjudge.net)
1.这道题目很简单就是求出对于长宽,多出来也不要少的a的倍数,相乘即可。
#include
int main()
{
long long n,m,a,res,i,j;
scanf("%lld%lld%lld",&n,&m,&a);
i=n/a;
if(n%a!=0) i+=1;
j=m/a;
if(m%a!=0) j+=1;
res=i*j;
printf("%lld\n",res);
return 0;
} 第三次题组 [Cloned] - Virtual Judge (vjudge.net)
1.这道题,其实是在求 n 到 1的区间内最多有几个 数字既要被n整除,又要能把前面整除
2.只要从1开始往后找最小的一个倍数,能够满足上面的条件即可。
#include
#define Maxsize 1000010
int a[Maxsize];
int main()
{
//找公因子
int n,num=1,j=0,cur,k=0;
scanf("%d",&n);
while(num=0;j--)
{
printf("%d ",a[j]);
}
} 第三次题组 [Cloned] - Virtual Judge (vjudge.net)
1. 暴力即可
#include
#define Maxsize 100010
int a[Maxsize];
int main()
{
long long n,i,j,sum1=0,sum2=0;
scanf("%lld",&n);
for(i=0;i=0;)
{
if(sum1>sum2)
{
sum2+=a[j];
j--;
}
else if(sum2>sum1)
{
sum1+=a[i];
i++;
}
else
{
sum1+=a[i];
sum2+=a[j];
i++;
j--;
}
}
if(i==j&&sum1==sum2)
{
i++;
}
else if(i==j&&sum1 第三次题组 [Cloned] - Virtual Judge (vjudge.net)
1.这个题目,搞了很久才懂得题目意思(是因为没有认真看)
2.题目很简单,就是说,给出的直线必须满足,是俩条平行于x轴和y轴的直线,不算是直线,是线段,线段的端点必须要被俩条直线都包含,是包含,更严格一点是端点必须在这些坐标中出现俩次。下面这样就不算,必须规规矩矩是一个矩形。
#include
typedef struct node
{
int x1,y1,x2,y2;
}NODE;
int main()
{
int i,j,m=0,n=0,f=0,k=0;
int a[8][2]={0},count[8]={0};
NODE p[4];
for(i=0;i<4;i++)
{
scanf("%d%d%d%d",&p[i].x1,&p[i].y1,&p[i].x2,&p[i].y2);
if(p[i].x1==p[i].x2&&p[i].y1==p[i].y2) f=1;
else if(p[i].x1==p[i].x2)
{
m++;
//与y轴平行
}
else if(p[i].y1==p[i].y2)
{
n++;
//与x轴平行
}
else f=1;
for(j=0;j=k)
{
a[j][0]=p[i].x1;
a[j][1]=p[i].y1;
count[j]++;
k++;
}
for(j=0;j=k)
{
a[j][0]=p[i].x2;
a[j][1]=p[i].y2;
count[j]++;
k++;
}
}
if(f||k!=4)
{
puts("NO");
return 0;
}
if(m!=2&&n!=2)
{
puts("NO");
return 0;
}
for(i=0;i<4;i++)
{
if(count[i]!=2)
{
puts("NO");
return 0;
}
}
puts("YES");
return 0;
} 第三次题组 [Cloned] - Virtual Judge (vjudge.net)
1.这是求负数在m内个数字能取得最大的和
2.排序计算即可。
#include
#include
#define Maxsize 110
using namespace std;
int main()
{
int n,m,i,x,j=0,res=0;
int a[Maxsize];
scanf("%d%d",&n,&m);
//n是电视的数量,m是bob能拿的数量
for(i=0;i 第三次题组 [Cloned] - Virtual Judge (vjudge.net)
1.这道题也是排序,然后看对应b的数组是不是递增的就行
#include
#include
#define Maxsize 100010
using namespace std;
typedef struct node
{
int a,b;
}NODE;
bool cmp(NODE x,NODE y)
{
if(x.a 第三次题组 [Cloned] - Virtual Judge (vjudge.net)
1.注意这道题说的是至少有几个说谎的人,而不是一定有几个人。
2.所有我们计数,再计算和,判断,减去这些说真话,剩下就是说谎话的。
#include
#define Maxsize 110
int main()
{
int t,n,i,j,k;
int a[Maxsize];
scanf("%d",&t);
while(t--)
{
int flag=-1;
int count[Maxsize]={0};
scanf("%d",&n);
for(i=0;i