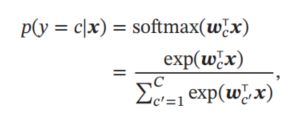Softmax回归简介

softmax回归简介

Softmax回归也称多项或多类的Logistic回归，是Logistic回归在多分类问题上的推广。

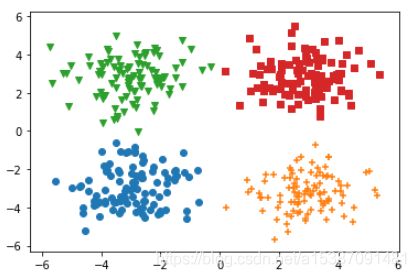
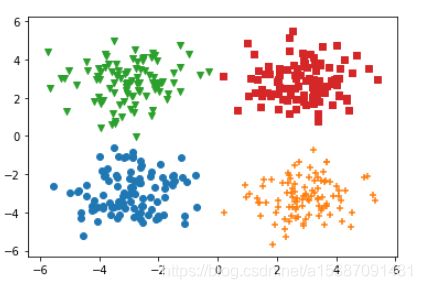
对于这样的一个数据分布，我们希望有一种方法能够将这组数据分成四类。

很显然，我们用四根直线就可以将这组数据划分开。

softmax回归与Logistic回归的不同之处就是softmax回归要面对的是两类以上的分类问题，一般的认为，要进行的分类问题有几种类型，就需要绘制几条直线，每条直线的作用是“将某一类与其他所有类区分开①”。

①所描述的正是一种一对多余的思想。

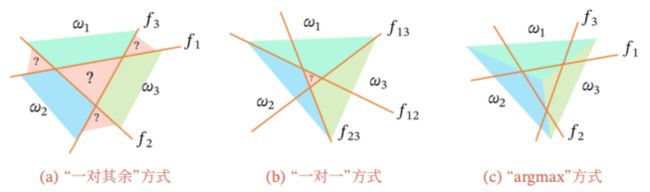
如何设计一个多分类的线性判别函数？

• 一对其余
• 一对一
• argmax

一对其余

把多分类问题转换为C个“一对其余”的二分类问题。这样的方式需要C个判别函数，C指需要区分的类别的个数。其中第c个判别函数fc是将类别c的数据样本和其他所有不属于c的数据样本分开。

一对一

把多分类问题转换为C(C-1)/2个“一对一”的二分类问题。这种方式需要C(C-1)/2个判别函数，其中第(i,j)个判别函数是把类别i和类别j的数据样本分开。

argmax

argmax是一种改进的“一对其余”方式，同样需要C个判别函数。

这C个判别函数的通式是：
$$f_c(x:w_c)=w_c^{T}x+b_c,c\in \{1,\cdots ,C\}$$
对于一个样本x，如果存在一个类别c，相对于其他所有类别$\tilde{c}$($\tilde{c}$≠c)有$f_c(x;w_c)$>KaTeX parse error: Got function '\tilde' with no arguments as subscript at position 3: f_\̲t̲i̲l̲d̲e̲{c}(x;w\tilde{c… ，那么x就是属于类别c的。

对于函数$f_c(x;w_c)$，我们可以理解为它表示样本点$x_i$关于这C条直线（C个判别函数）的距离判别。

我们先看一下三种判别方式能得到的区分效果。

可以看到，无论是“一对其余”还是“一对一”方式，都会有盲区。而且“argmax”方式对前面两种方式做了改进，使得这些盲区内的数据也可以被区分。

我们可以将argmax方式的判别函数看成是欧式距离的计算，显然，即使是“盲区”内的数据点，这些数据点关于直线的欧式距离是一定存在的，所以它一定是可以被划分的，所以在一定程度上解决了这个问题。

one-hot编码

Logistic回归输出的是一个范围为[0,1]的概率值，是因为Logistic回归面对的二分类问题，一个范围在[0,1]内的概率值可以明确的区分输出的结果是0类还是1类。

然而在softmax回归中，多类问题使分类结果的表示变得困难起来。

所以会对输出结果y进行one-hot编码，进行编码后使得这个结果y_hot可以清晰的表示结果所属的类别。

那么什么是one-hot编码呢？

我们直观的拿一个例子：

假设四分类问题中分类为1，2，3，4四类，分类y=1经过one-hot编码后，得到的结果是[1,0,0,0]。

是的，它是一个数组，或者说是一个向量。

那么同样的，分类y=2经过one-hot编码后得到的结果是[0,1,0,0]，以此类推。

当然，在实际进行参数训练后得到的结果不可能是这么精确的值，我们知道分类问题得到的都是一些概率值。

所以我们得到的值可能是y1 = [0.1,0.2,0.5,0.2]，y2 = [0.7,0.1,0.1,0.1]…

不过结果依然很显然了，y1表示这个数据更趋向于3类，y2表示的数据更趋向于1类。

softmax用到的函数

• softmax激活函数
• one-hot编码
• 交叉熵损失函数
• 梯度下降法

与Logistic回归不同的是激活函数，softmax回归用到的激活函数是softmax。

softmax和sigmoid函数的目的都是将$w_1\ast x_1+w_2\ast x_2+b$得到的值进行一个归一化，将值压缩到区间(0,1)内，这样便于所有的值进行比较。

代码实现

1. 引入所需库

   import numpy as np
   import matplotlib.pyplot as plt
   

2. 随机生成数据集

   np.random.seed(0)
   Num=100
   #0类别
   x1 = np.random.normal(-3,1,size=(Num))
   x2 = np.random.normal(-3,1,size=(Num))
   y= np.zeros(Num)
   data0 = np.array([x_1,x_2,y])
   #1类别
   x1 = np.random.normal(3,1,size=(Num))
   x2 = np.random.normal(-3,1,size=(Num))
   y= np.ones(Num)
   data1 = np.array([x_1,x_2,y])
   #2类别
   x1 = np.random.normal(-3,1,size=(Num))
   x2 = np.random.normal(3,1,size=(Num))
   y= np.ones(Num)*2
   data2 = np.array([x_1,x_2,y])
   #3类别
   x1 = np.random.normal(3,1,size=(Num))
   x2 = np.random.normal(3,1,size=(Num))
   y= np.ones(Num)*3
   data3 = np.array([x_1,x_2,y])
   data0 = data0.T
   data1 = data1.T
   data2 = data2.T
   data3 = data3.T
   

3. 查看数据分布

   plt.scatter(data0[:,0],data0[:,1],marker="o")
   plt.scatter(data1[:,0],data1[:,1],marker="+")
   plt.scatter(data2[:,0],data2[:,1],marker="v")
   plt.scatter(data3[:,0],data3[:,1],marker="s")
   

   

4. 随机初始化权值与偏置

   W = np.random.rand(4,2)
   b = np.random.rand(4,1)
   

5. 打乱数据集

   All_data=np.concatenate((data0,data1,data2,data3))
   np.random.shuffle(All_data)
   

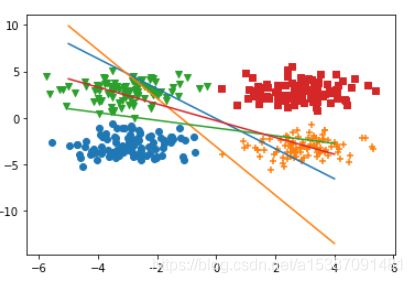
6. 查看初始化后判别函数的情况

   x=np.arange(-5,5)
   y1=(-W[0,0]*x-b[0])/W[0,1]
   y2=(-W[1,0]*x-b[1])/W[1,1]
   y3=(-W[2,0]*x-b[2])/W[2,1]
   y4=(-W[3,0]*x-b[3])/W[3,1]
   plt.scatter(data0[:,0],data0[:,1],marker="o")
   plt.scatter(data1[:,0],data1[:,1],marker="+")
   plt.scatter(data2[:,0],data2[:,1],marker="v")
   plt.scatter(data0[:,0],data3[:,1],marker="s")
   plt.plot(x,y1)
   plt.plot(x,y2)
   plt.plot(x,y3)
   plt.plot(x,y4)
   

   

7. 定义函数

   #softmax(x)=e^x/sum(e^x)
   def softmax_matrix(z):#当z不是一维时
       exp = np.exp(z)
       sum_exp = np.sum(np.exp(z),axis=1,keepdims=True)
       return exp/sum_exp
   def softmax_vector(z):#当z是一维时
       return np.exp(z)/np.sum(np.exp(z))
   #对Y进行one-hot编码
   #temp = {0,1,2,3}
   def one_hot(temp):
       one_hot = np.zeros((len(temp),len(np.unique(temp))))
       one_hot[np.arange(len(temp)),temp.astype(np.int).T]=1 
       return one_hot
   # 计算 y_hat
   def compute_y_hat(W,X,b):
       return np.dot(X,W.T)+b.T
   #计算交叉熵
   def cross_entropy(y,y_hat):
       loss = -(1/len(y))*np.sum(y*np.log(y_hat))
       return loss
   

8. 进行训练

   #w = w + lr*grad
   lr = 0.01
   loss_list=[]
   for i in range(1000):
       #计算loss
       y_hat = softmax_matrix(compute_y_hat(W,train_data_X,b))
       y = one_hot(train_data_Y)
       loss = cross_entropy(y,y_hat)
       loss_list.append(loss)
       #计算梯度
       grad_w = (1/len(train_data_X))*(np.dot(train_data_X.T,(y-y_hat)).T)
       grad_b = (1/len(train_data_X))*np.sum(y-y_hat)
       #更新参数
       W = W + lr*grad_w
       b = b + lr*grad_b
       # 输出
       if i%100==1 :
           print("i:%d , loss:%f"%(i,loss))
   

   

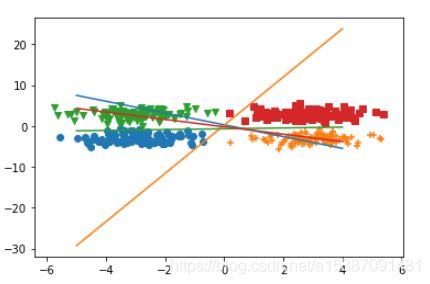
9. 绘制训练后的分类情况

   x=np.arange(-5,5)
   y1=(-W[0,0]*x-b[0])/W[0,1]
   y2=(-W[1,0]*x-b[1])/W[1,1]
   y3=(-W[2,0]*x-b[2])/W[2,1]
   y4=(-W[3,0]*x-b[3])/W[3,1]
   plt.scatter(data0[:,0],data0[:,1],marker="o")
   plt.scatter(data1[:,0],data1[:,1],marker="+")
   plt.scatter(data2[:,0],data2[:,1],marker="v")
   plt.scatter(data3[:,0],data3[:,1],marker="s")
   plt.plot(x,y1)
   plt.plot(x,y2)
   plt.plot(x,y3)
   plt.plot(x,y4)
   

   

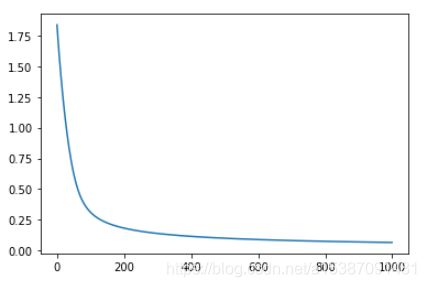
10. 查看loss值下降曲线

    plt.plot(loss_list)