K-means聚类分析(鸢尾花)

一、实验原理

        k-means算法是最为经典的基于划分的聚簇方法，是十大经典数据挖掘算法之一。简单地说k-means就是在没有任何监督信号的情况下将数据分为k份的一种方法。k-means算法的基本思想为：在数据集中根据一定策略选择k个点作为每个簇的初始中心，然后观察剩余的数据，将数据划分到距离这k个点最近的簇中，也就是说将数据划分成k个簇完成一次划分，但形成的新簇并不一定是最好的划分，因此生成的新簇中，重新计算每个簇的中心点，然后在重新进行划分，直到每次划分的结果保持不变。

算法步骤如下：

1) 随机选择K个中心点

2) 把每个数据点分配到离它最近的中心点；

3) 重新计算每类中的点到该类中心点距离的平均值;

4) 分配每个数据到它最近的中心点；

5) 重复步骤3和4，直到所有的观测值不再被分配或是达到最大的迭代次数.

二、源代码

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import math
import numpy as np


def getData(feature1, feature2):
    iris = load_iris()
    X = np.array([[x[feature1]] for x in iris.data])
    Y = np.array([[x[feature2]] for x in iris.data])
    dataSet = np.hstack((X, Y))
    names = iris.feature_names
    return dataSet, names


def calcMeans(catagory_k):  # 计算簇内均值
    length = len(catagory_k)
    if length == 0:
        return 0, 0
    sum_x = 0
    sum_y = 0
    for i in range(length):
        sum_x += catagory_k[i][0]
        sum_y += catagory_k[i][1]
    mean = (sum_x / length, sum_y / length)
    return mean


def calEnclidean(x1, x2):  # 计算欧氏距离
    return math.sqrt(math.pow((x1[0] - x2[0]), 2) + math.pow((x1[1] - x2[1]), 2))


def minDistance(example, means, k):  # 计算出距离哪个簇最近
    min = calEnclidean(example, means[0])  # 设离第一个最近
    cluster_k = 0
    for i in range(k):
        if calEnclidean(example, means[i]) < min:
            min = calEnclidean(example, means[i])
            cluster_k = i
    return cluster_k  # 返回簇的下标


def calcSame(label_temp, label_pred):   # 判断聚类结果是否发生变化
    if len(label_pred) != len(label_temp):
        return 0
    for j in range(len(label_temp)):
        if label_temp[j] != label_pred[j]:
            return 0
    return 1


def randCent(data, k):
    n = np.shape(data)[1]  # 得到数据样本的维度
    centroids = np.mat(np.zeros((k, n)))  # 初始化为一个(k, n)的全零矩阵
    for j in range(n):
        minJ = np.min(data[:, j])  # 得到该列数据的最小值和最大值
        maxJ = np.max(data[:, j])
        rangeJ = float(maxJ - minJ)
        centroids[:, j] = minJ + rangeJ * np.random.rand(k, 1)  # k * 1 的矩阵（第j列）
    return centroids


def KMeans(data, k):
    length = len(data)
    label_pred = []     # 保存聚类结果
    label_temp = []
    means = randCent(data, k)  # 初始化means
    means = means.tolist()  # 将矩阵转为列表
    for x in range(100):  # 聚类100次之后就终止
        label_pred = label_temp
        label_temp = []
        catagory = [[] for i in range(k)]  # k个簇
        for i in range(length):  # 判断每一个二元组属于哪一类
            cluster_k = minDistance(data[i], means, k)  # 分类结果（簇）的下标
            catagory[cluster_k].append(data[i])  # 对应簇添加元素
            label_temp.append(cluster_k)  # 添加分类结果
        means = [calcMeans(catagory[i]) for i in range(k)]  # 新的means
        ret = calcSame(label_temp, label_pred)  # 如果连续两次的聚类结果没有变化则退出循环
        if ret == 1:
            break
    return np.array(label_pred)


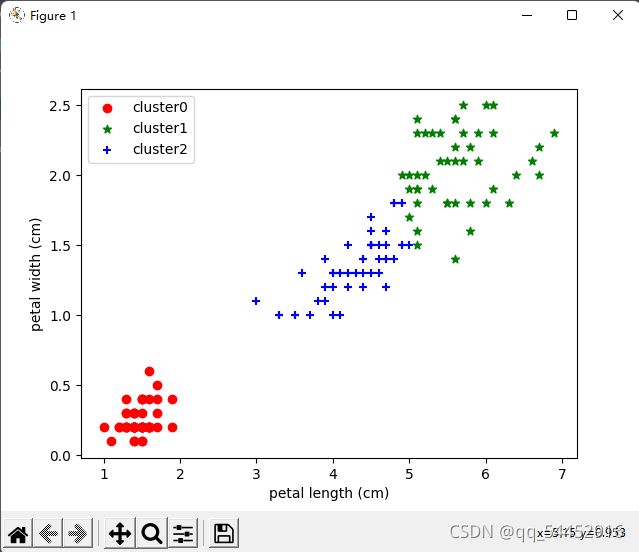
def drawScatter(data, label_pred, names1, names2):  # 绘制散点图
    x0 = data[label_pred == 0]
    x1 = data[label_pred == 1]
    x2 = data[label_pred == 2]
    ax = plt.subplot()
    ax.scatter(x0[:, 0], x0[:, 1], c = "red", marker = 'o', label = 'cluster0')
    ax.scatter(x1[:, 0], x1[:, 1], c = "green", marker = '*', label = 'cluster1')
    ax.scatter(x2[:, 0], x2[:, 1], c = "blue", marker = '+', label = 'cluster2')
    plt.xlabel(names1)
    plt.ylabel(names2)
    plt.legend()
    plt.show()


if __name__ == '__main__':
    feature1 = 2  # 前一个特征
    feature2 = 3  # 后一个特征
    data, names = getData(feature1, feature2)
    k = 3  # 簇的数量
    label_pred = KMeans(data, k)
    drawScatter(data, label_pred, names[feature1], names[feature2])

三、实验结果