一元线性回归
基本形式
f ( x ) = w 1 x 1 + w 2 x 2 + ⋯ + w d x d + b f(x)=w_1x_1+w_2x_2+\cdots+w_dx_d+b f(x)=w1x1+w2x2+⋯+wdxd+b
一般向量形式写成
f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b
其中 w = ( w 1 ; w 2 ; ⋯ ; w d ) w=(w_1;w_2;\cdots;w_d) w=(w1;w2;⋯;wd), w w w和 b b b学得之后,模型就得以确定
许多功能更为强大的非线性模型可在线性模型的基础上通过引入层级结构或高维映射而得,w也直观的表达了各属性在预测中的重要性
例如: f 好瓜 ( x ) = 0.2 ⋅ x 色泽 + 0.5 ⋅ x 根蒂 + 0.3 ⋅ x 敲声 + 1 f_{好瓜}(x)=0.2 \cdot x_{色泽}+0.5 \cdot x_{根蒂}+0.3 \cdot x_{敲声}+1 f好瓜(x)=0.2⋅x色泽+0.5⋅x根蒂+0.3⋅x敲声+1,则意味着其中根蒂最要紧,而敲声比色泽更重要
线性回归
给定数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x m , y m ) } D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)\} D={(x1,y1),(x2,y2),⋯,(xm,ym)},其中 x i = ( x i 1 ; x i 2 ; ⋯ ; x i d ) , y i ∈ R x_i=(x_{i1};x_{i2};\cdots;x_{id}),y_i \in \R xi=(xi1;xi2;⋯;xid),yi∈R,“线性回归”试图学得一个线性模型以尽可能准确地预测实值输出标记
对离散属性,若属性值间存在“序”关系,可通过连续化将其转化为连续值,例如二值属性“身高”的取值,“高”“矮”可转化为{1.0,0.0},三值属性“高度”的取值“高”,“中”,“低”可转化为{1.0,0.5,0.0};若属性值间不存在序关系,假定有k个属性值,则通常转化为k维向量,例如属性“瓜类”的取值,“西瓜”“南瓜”“黄瓜”可转化为(0,0,1),(0,1,0),(1,0,0)
线性回归试图学得: f ( x i ) = w x i + b f(x_i)=wx_i+b f(xi)=wxi+b,使得 f ( x i ) ≃ y i f(x_i) \simeq y_i f(xi)≃yi
注意:
因为这里我们需要的是预测结果与实际结果的最小值,需要用到的是线性回归
正交回归:找的是点到直线的垂直距离
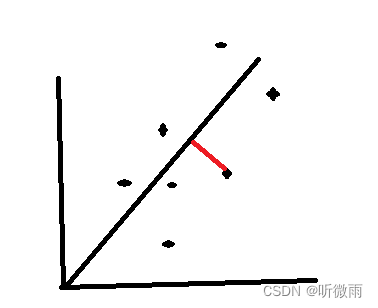
线性回归:找的是点到直线的竖直距离
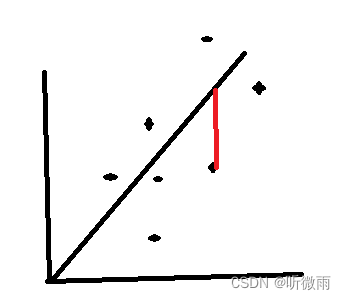
均方误差
均方误差是回归任务重最常用的性能度量,因此我们可通过均方误差,来获得使均方误差最小的 w w w和 b b b的值
( w ∗ , b ∗ ) = a r g m i n ( w , b ) ∑ i = 1 m ( f ( x i ) − y i ) 2 = a r g m i n ( w , b ) ∑ i = 1 m ( y i − w x i − b ) 2 (w^*,b^*)=argmin_{(w,b)} \sum_{i=1}^m (f(x_i)-y_i)^2 \\ =argmin_{(w,b)} \sum_{i=1}^m (y_i-wx_i-b)^2 (w∗,b∗)=argmin(w,b)i=1∑m(f(xi)−yi)2=argmin(w,b)i=1∑m(yi−wxi−b)2
均方误差对应了常用欧几里得距离(欧氏距离)。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。在线性回归里,最小二乘法就是找到一条直线,使所有样本到直线的欧式距离之和最小
最小二乘的参数估计
求解 w w w和 b b b使 E ( w , b ) = ∑ i = 1 m ( y i − w x i − b ) 2 E(w,b)= \sum_{i=1}^m(y_i-wx_i-b)^2 E(w,b)=∑i=1m(yi−wxi−b)2最小化的过程,称为线性回归模型的“参数估计”
凸函数
这里 E ( w , b ) E(w,b) E(w,b)是关于 w w w和 b b b的凸函数,当它关于 w w w和 b b b的导数均为零时,得到 w w w和 b b b的最优解
对区间 [ a , b ] [a,b] [a,b]上定义的函数 f f f,若它对区间中任意两点 x 1 , x 2 x_1,x_2 x1,x2均有 f ( x 1 + x 2 2 ) ≤ f ( x 1 ) + f ( x 2 ) 2 f( \frac{x_1+x_2}{2}) \leq \frac{f(x_1)+f(x_2)}{2} f(2x1+x2)≤2f(x1)+f(x2),则称 f f f为区间 [ a , b ] [a,b] [a,b]上的凸函数
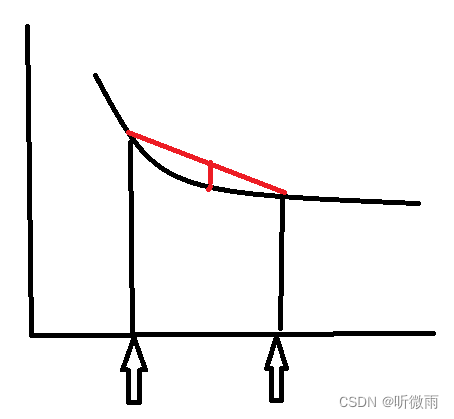
U形曲线的函数如 f ( x ) = x 2 f(x)=x^2 f(x)=x2,通常是凸函数
对实数集上的函数,可通过求二阶导数来判别:若二阶导数在区间上非负,则成为凸函数;若二阶导数在区间上恒大0,则称为严格凸函数
求导解 w , b w,b w,b
E ( w , b ) = ∑ i = 1 m ( y i − w x i − b ) 2 E(w,b)=\sum_{i=1}^m (y_i-wx_i-b)^2 E(w,b)=∑i=1m(yi−wxi−b)2
对 w w w求偏导
∂ E ( w , b ) ∂ w = 2 ( w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i ) 令 2 ( w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i ) = 0 ,求出最优的解 因 b = y ‾ − w x ‾ 故将 b 代入上式得 2 ( w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − y ‾ + w x ‾ ) x i ) = 0 展开得 w ∑ i = 1 m x i 2 − ∑ i = 1 m y i x i + ∑ i = 1 m y ‾ x i − ∑ i = 1 m w x ‾ x i = 0 对其进行取 w 得: w = ∑ i = 1 m y i x i − ∑ i = 1 m y ‾ x i ∑ i = 1 m x i 2 − ∑ i = 1 m x ‾ x i 因为: ∑ i = 1 m y ‾ x i = 1 m ( y 1 + y 2 + ⋯ + y m ) ( x 1 + x 2 + ⋯ + x m ) = ∑ i = 1 m y i x ‾ 又因为 ∑ i = 1 m x ‾ x i = 1 m ( x 1 + x 2 + ⋯ + x m ) ( x 1 + x 2 + ⋯ + x m ) = 1 m ( ∑ i = 1 m x i ) 2 综上: w = ∑ i = 1 m y i ( x i − x ‾ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 \frac{\partial E(w,b)}{\partial w}=2(w \sum_{i=1}^m x_i^2-\sum_{i=1}^m(y_i-b)x_i) \\ 令2(w \sum_{i=1}^m x_i^2-\sum_{i=1}^m(y_i-b)x_i)=0,求出最优的解 \\ 因b=\overline y-w\overline x \\ 故将b代入上式得2(w \sum_{i=1}^m x_i^2-\sum_{i=1}^m(y_i-\overline y+w\overline x)x_i)=0 \\ 展开得w \sum_{i=1}^m x_i^2-\sum_{i=1}^my_ix_i+\sum_{i=1}^m \overline yx_i- \sum_{i=1}^m w\overline xx_i=0 \\ 对其进行取w得:w=\frac{\sum_{i=1}^my_ix_i-\sum_{i=1}^m \overline yx_i}{ \sum_{i=1}^m x_i^2-\sum_{i=1}^m \overline xx_i} \\ 因为:\sum_{i=1}^m \overline yx_i=\frac{1}{m}(y_1+y_2+\cdots+y_m)(x_1+x_2+\cdots+x_m)=\sum_{i=1}^m y_i \overline x\\ 又因为\sum_{i=1}^m \overline xx_i=\frac{1}{m}(x_1+x_2+\cdots+x_m)(x_1+x_2+\cdots+x_m)=\frac{1}{m}(\sum_{i=1}^m x_i)^2 \\ 综上:w=\frac{\sum_{i=1}^my_i(x_i-\overline x)}{ \sum_{i=1}^m x_i^2-\frac{1}{m}(\sum_{i=1}^m x_i)^2} ∂w∂E(w,b)=2(wi=1∑mxi2−i=1∑m(yi−b)xi)令2(wi=1∑mxi2−i=1∑m(yi−b)xi)=0,求出最优的解因b=y−wx故将b代入上式得2(wi=1∑mxi2−i=1∑m(yi−y+wx)xi)=0展开得wi=1∑mxi2−i=1∑myixi+i=1∑myxi−i=1∑mwxxi=0对其进行取w得:w=∑i=1mxi2−∑i=1mxxi∑i=1myixi−∑i=1myxi因为:i=1∑myxi=m1(y1+y2+⋯+ym)(x1+x2+⋯+xm)=i=1∑myix又因为i=1∑mxxi=m1(x1+x2+⋯+xm)(x1+x2+⋯+xm)=m1(i=1∑mxi)2综上:w=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−x)
对 b b b求偏导
∂ E ( w , b ) ∂ b = 2 ( ∑ i = 1 m b − ∑ i = 1 m ( y i − w x i ) ) 因为: ∑ i = 1 m b = m b 所以: ∂ E ( w , b ) ∂ b = 2 ( m b − ∑ i = 1 m ( y i − w x i ) ) 令 2 ( m b − ∑ i = 1 m ( y i − w x i ) ) = 0 m b − ∑ i = 1 m ( y i − w x i ) = 0 b = 1 m ∑ i = 1 m ( y i − w x i ) \frac{\partial E(w,b)}{\partial b}=2(\sum_{i=1}^mb-\sum_{i=1}^m(y_i-wx_i)) \\ 因为:\sum_{i=1}^mb=mb \\ 所以:\frac{\partial E(w,b)}{\partial b}=2(mb-\sum_{i=1}^m(y_i-wx_i)) \\ 令2(mb-\sum_{i=1}^m(y_i-wx_i))=0 \\ mb-\sum_{i=1}^m(y_i-wx_i)=0 \\ b=\frac{1}{m}\sum_{i=1}^m(y_i-wx_i) ∂b∂E(w,b)=2(i=1∑mb−i=1∑m(yi−wxi))因为:i=1∑mb=mb所以:∂b∂E(w,b)=2(mb−i=1∑m(yi−wxi))令2(mb−i=1∑m(yi−wxi))=0mb−i=1∑m(yi−wxi)=0b=m1i=1∑m(yi−wxi)
通过上述上述求解过程我们得到了 w w w和 b b b的最优解的闭式:
w = ∑ i = 1 m y i ( x i − x ‾ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 b = 1 m ∑ i = 1 m ( y i − w x i ) w=\frac{\sum_{i=1}^my_i(x_i-\overline x)}{ \sum_{i=1}^m x_i^2-\frac{1}{m}(\sum_{i=1}^m x_i)^2} \\ b=\frac{1}{m}\sum_{i=1}^m(y_i-wx_i) w=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−x)b=m1i=1∑m(yi−wxi)