17 条件随机场

17 条件随机场——CRF（Condition Random Field）

17.1 背景介绍

从分类问题开始探讨，分类问题包含两部分，硬分类和软分类问题：

• 硬分类：
  1. SVM：通过几何间隔最大化实现分类
  2. PLA：通过错误驱动的感知机
  3. Linear Discriminant Analysis：类内小类间大的思想分类
• 软分类：又分成了概率判别模型与概率生成模型
  • 概率判别模型
    1. Logistic Regression：通过对P(Z|X)建模进行求解
    2. Maximum Entropy Model：最大熵原理证明是指数族分布
  • 概率生成模型
    1. Naives Bayes：通过朴素贝叶斯假设减少计算量
    2. Gaussian Mixture Model：将数据看为由多个高斯分布组成的混合模型
    3. Hidden Markov Model：建立齐次Markov假设+观测独立假设实现时间序列的模型

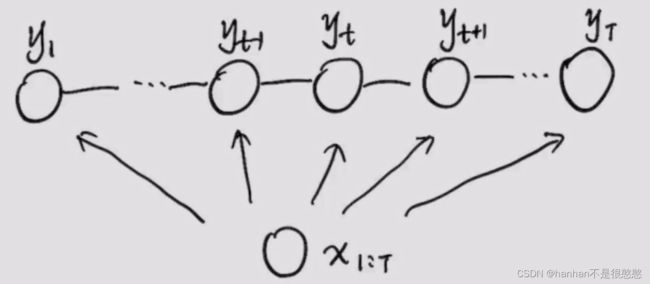
本章通过打破了HMM的观测独立假设，实现了MEMM的概率判别模型，将数据关系变成如下图的形式：

但MEMM本身由于局部归一化的问题，会有标注偏差问题（label bias problem），所以为了解决这个问题提出了CRF的概率判别模型，数据关系转变为无向图，如下：

17.2 HMM与MEMM的区别

这一节主要讲我们是怎么从HMM过渡到MEMM的，以及我们为什么要过渡到MEMM。

首先我们分点介绍一下HMM：

1. HMM构造了两个假设：齐次一阶Markov假设（齐次是指隐状态变化与时间无关，只与转移矩阵相关，一阶是指链式）、观测独立假设

2. HMM中我们对$P(X,Z|\lambda )$建模，是概率生成模型

3. 通过因子分解，我们可以讲HMM的联合概率公式简化为：
   $$P(X,Z|\lambda )=\prod _{t=1}^{T}P(x_t,z_t|\lambda )=P(x_1|z_1,\lambda )\prod _{t=2}^{T}P(z_t|z_{t-1},\lambda )P(x_t|z_t,\lambda )$$

但是为让模型更加精确，我们提出了MEMM模型，然后介绍一下MEMM：

1. MEMM中我们打破了观测独立假设，每个隐状态都与全部观测变量相关：
   

2. MEMM是概率判别模型，对$P(Z|X,\lambda )$建模

3. 同样通过因子分解，MEMM的先验公式为：
   $$P(Z|X,\lambda )=P(Z_1|x_{1:T},\lambda )\cdot \prod _{t=2}^{T}P(z_t|z_{t-1},x_{1:T},\lambda )$$

相较于HMM，MEMM有两个主要的优点：

1. 观测独立假设本身就是为了便于计算提出的，打破后更加合理
2. 在链式模型中，概率判别模型更合适，也可以节省计算

17.3 MEMM与CRF的区别

在通过17.2中，打破了观测独立假设，使得模型更加合理。我们自然就会想到，齐次Markov假设是否也需要打破呢？MEMM又有什么缺点，又会出现什么问题呢？

首先我们来介绍一下MEMM究竟会有什么问题：

• MEMM的缺点是label bias problem（标注偏差问题），这个问题由John Lafferty在关于CRF的论文中提出。

• 问题出现的原因是每次到了新的时间后，会进行归一化，减少了多样性。

• 假设有这样一个具体的例子，我们在给单词做训练：

  

• 我们在训练集中，给出了3个rob和1个rib，训练的结果自然是：
  $$\{\begin{array}{l}P(1|0,r)=0.25\\ P(3|0,r)=0.75\end{array}$$
  但由于前面的情况都是$r$​，所以在1、3处做归一化后，后面使得（不太清楚为啥）：
  $$\{\begin{array}{ll}P(2|1,r)=1& P(5|2,r)=1\\ P(4|3,r)=1& P(5|4,r)=1\end{array}$$

• 所以如果当前有一个Decoding问题：
  $$\hat{Y}=arg\underset{y_1,y_2,y_3}{\max }P(y_1,y_2,y_3|rib)$$

• 在给出rib的条件后会得出rob的结果。

而CRF解决了这个问题

17.4 CRF模型

上文一直是在介绍为什么要用CRF，以及CRF的合理性。本节开始介绍具体的CRF模型。

17.4.1 CRF的概率密度函数

CRF也叫条件随机场：

• 条件：概率判别式模型$P(Y|X)$
• 随机场：Markov随机场——无向图模型
• 图像表示为：
  

所以现在的重要任务就是将条件概率的表示方法写出来。回忆我们在Markov Random Field中学习的因子分解：

• 将无向图模型分解为最大团的集合（因为无向图的节点只与邻居相关）：
  $$P(X)=\frac{1}{Z}\prod _{i=1}^K{\phi }_i(X_{C_i})=\frac{1}{Z}\prod _{i=1}^K\exp [-E_i(X_{C_i})]=\frac{1}{Z}\exp \sum _{i=1}^K{F}_i(X_{C_i})$$
  其中${\phi }_i(X_{C_i})$表示势函数，$E_i(X_{C_i})$表示能量函数

根据上文的因式分解，可以将$P(Y|X)$​写为：
$$P(Y|X)=\frac{1}{Z}\exp \sum _{i=1}^K{F}_i(X_{C_i})$$
此时我们的应用场景是CRF，CRF的无向图是链式的，所以在$N$个节点的情况下，最大团是$N-1$个，为了简化公式，我们假设节点有$y_0$​的存在：
$$P(Y|X)=\frac{1}{Z}\exp \sum _{t=1}^{T}F(y_{t-1},y_t,x_{1:T})$$
为了继续简化，我们给出一些方法：

简化到这里，我们觉得$F(y_{t-1},y_t,x_{1:T})$还是太大了，所以我们想要把ta划分为几个部分（用$\Delta$​表示某一部分的函数）：
$$F(y_{t-1},y_t,x_{1:T})={\Delta }_{y_{t-1},x_{1:T}}+{\Delta }_{y_t,x_{1:T}}+{\Delta }_{y_{t-1},y_t,x_{1:T}}$$
我们发现，其实${\Delta }_{y_{t-1},x_{1:T}}$的部分，也会表示在$F(y_{t-2},y_{t-1},x_{1:T})$中，为求简化，我们删除这一部分（${\Delta }_{y_t,x_{1:T}}$​系数不变是因为可以放在函数里面所以不表示）：
$$F(y_{t-1},y_t,x_{1:T})={\Delta }_{y_t,x_{1:T}}+{\Delta }_{y_{t-1},y_t,x_{1:T}}$$
然后就是将${\Delta }_{y_t,x_{1:T}}$与${\Delta }_{y_{t-1},y_t,x_{1:T}}$通过函数表示出来，我们这样假设：
$$\{\begin{array}{l}{\Delta }_{y_{t-1},y_t,x_{1:T}}={\sum }_{k=1}^K{\lambda }_k{f}_k(y_{t-1},y_t,x_{1:T})\\ {\Delta }_{y_t,x_{1:T}}={\sum }_{l=1}^L{\eta }_l{g}_l(y_t,x_{1:T})\end{array}$$
其中${\lambda }_k$和${\eta }_l$表示我们需要学习的参数，$f_k$和$g_l$表示给定的特征函数（根据一定条件给出特定值的函数，如sigmoid函数），$K$、$L$是已知的（因为他表示特征函数的可能性）。
例如：问题是一句话“我爱中国”，特征函数$f_k$表示其中词语的词性{名词、动词、副词、···}，K就表示集合的大小。

根据以上方法，我们可以得到公式：
$$P(Y|X)=\frac{1}{Z}\exp \sum _{t=1}^T\left[\sum _{k=1}^K{\lambda }_k{f}_k(y_{t-1},y_t,x_{1:T})+\sum _{l=1}^L{\eta }_l{g}_l(y_t,x_{1:T})\right]$$
至此我们给出了CRF的概率密度函数。

17.4.2 CRF概率密度函数简化（向量形式）

首先要讲一下为什么要简化？

• 矩阵运算相较于一般的累加运算要更快
• 在实际使用上看起来更清晰简单

然后我们简化的核心目的是什么？

• 删除所有的累加运算

所以首先我们可以将所有的变量都写成向量的形式：
y = ( y 1 y 2 … y T ) x = ( x 1 x 2 … x T ) λ = ( λ 1 λ 2 … λ T ) η = ( η 1 η 2 … η K ) y = \begin{pmatrix} y_1 \\ y_2 \\ \dots \\ y_T \\ \end{pmatrix} \quad x = \begin{pmatrix} x_1 \\ x_2 \\ \dots \\ x_T \\ \end{pmatrix} \quad \lambda = \begin{pmatrix} \lambda_1 \\ \lambda_2 \\ \dots \\ \lambda_T \\ \end{pmatrix} \quad \eta = \begin{pmatrix} \eta_1 \\ \eta_2 \\ \dots \\ \eta_K \\ \end{pmatrix} y= ​y1​y2​…yT​​ ​x= ​x1​x2​…xT​​ ​λ= ​λ1​λ2​…λT​​ ​η= ​η1​η2​…ηK​​ ​

f = ( f 1 f 2 … f K ) = f ( y t − 1 , y t , x 1 : T ) g = ( g 1 g 2 … g L ) = g ( y t , x 1 : T ) f = \begin{pmatrix} f_1 \\ f_2 \\ \dots \\ f_K \\ \end{pmatrix} = f(y_{t-1}, y_t, x_{1:T}) \quad g = \begin{pmatrix} g_1 \\ g_2 \\ \dots \\ g_L \\ \end{pmatrix} = g(y_t, x_{1:T}) f= ​f1​f2​…fK​​ ​=f(yt−1​,yt​,x1:T​)g= ​g1​g2​…gL​​ ​=g(yt​,x1:T​)

所以原公式可以如此简化：
$$\begin{array}{rl}P(Y=y|X=x)& =\frac{1}{Z}\exp \sum _{t=1}^T\left[\sum _{k=1}^K{\lambda }_k{f}_k(y_{t-1},y_t,x_{1:T})+\sum _{l=1}^L{\eta }_l{g}_l(y_t,x_{1:T})\right]\\ & =\frac{1}{Z(x,\lambda ,\eta )}\exp \sum _{t=1}^T\left[{\lambda }^{T}f(y_{t-1},y_t,x_{1:T})+{\eta }^{T}g(y_t,x_{1:T})\right]\\ & =\frac{1}{Z(x,\lambda ,\eta )}\exp \left[{\lambda }^T\sum _{t=1}^{T}f(y_{t-1},y_t,x_{1:T})+{\eta }^T\sum _{t=1}^{T}g(y_t,x_{1:T})\right]\end{array}$$
如此便将求和符号删除，为了进一步简化公式，我们给出定义：
$$\theta ={\left(\begin{array}{c}\lambda \\ \eta \end{array}\right)}_{K+L}H={\left(\begin{array}{c}{\sum }_{t=1}^{T}f\\ {\sum }_{t=1}^{T}g\end{array}\right)}_{K+L}=H(y_t,y_{t-1},x_{1:T})$$
所以可以最终简化为：
$$P(Y=y|X=x)=\frac{1}{Z(x,\theta )}\exp ⟨\theta ,H⟩$$

17.5 CRF需要解决的问题

要求解CRF，还就是要求解概率图模型中的两大问题：

• Learning问题：
  1. parameter estimation——参数估计
• Inference问题：
  1. marginal problem——边缘概率求解：求$P(y_t)$
  2. conditional problem——后验求解：求$P(Y|X)$
  3. MAP Inference——decoding问题：求解最大后验概率状态序列，如HMM中

针对CRF来说，这些问题主要是求解：

• Learning问题：

  1. parameter estimation：在给定N组数据${\{(x^{(i)},y^{(i)})\}}_{i=1}^N$的条件下求$\hat{\theta }=arg\max {\prod }_{i=1}^{N}P(y^{(i)},x^{(i)})$

• Inference问题：

  1. marginal problem：求$P(y_t|x)$
  2. conditional problem：针对生成模型，因为$P(Y|X)$就是CRF的假设的分布，所以这个问题不用求
  3. MAP Inference：求解 $\hat{y}=arg{\max }_{y}P(Y|X)$，与HMM相同

17.6 边缘概率计算——marginal问题

在一般情况下，若要求解边缘概率，只需要将其他的未知量积分掉就行了，如：

• 已知后验为：
  $$P(Y|X)=\frac{1}{Z}\prod _{t=1}^T\phi (y_{t-1},y_t,X)$$

• 则通过积分求解边缘概率的结果为：
  $$\begin{array}{rl}P(y_t=i|X)& =\sum _{y_1\dots y_{t-1}{y}_{t+1}\dots y_T}P(Y|X)\\ & =\sum _{y_1\dots y_{t-1}}\sum _{y_{t+1}\dots y_T}\frac{1}{Z}\prod _{t=1}^T\phi (y_{t-1},y_t,X)\end{array}$$

其实到这一步已经可以求解了，但是积分的层次过高，连加与连乘的时间复杂度已经达到了指数级，所以基本等于无法求解。本节的主要工作就是通过递推的方法简化计算。

---

为简化计算，我们现在分析一下上面的公式，先做一些简单的变换：
$$\begin{array}{rl}P(y_t=i|X)& =\sum _{y_1\dots y_{t-1}}\sum _{y_{t+1}\dots y_T}\frac{1}{Z}\prod _{t=1}^T\phi (y_{t-1},y_t,X)\\ & =\frac{1}{Z}{\Delta }_{left}{\Delta }_{right}\end{array}$$
我们先分析一下左边的公式${\Delta }_{left}$：
$${\Delta }_{left}=\sum _{y_1\dots y_{t-1}}{\phi }_1(y_0,y_1,X)\cdots \cdot {\phi }_t(y_{t-1},y_t=i,X)$$
我们发现，一个积分最多与两个公式相关，所以可以把${\Delta }_{left}$写为：
$${\Delta }_{left}=\sum _{y_{t-1}}\left({\phi }_t(y_{t-1},y_t=i,X)\cdots \sum _{y_1}\left({\phi }_2(y_1,y_2,X)\sum _{y_0}{\phi }_1(y_0,y_1,X)\right)\right)$$
这里就能看出来${\Delta }_{left}$是嵌套关系，可以通过递推求解，我们假设${\Delta }_{left}={\alpha }_t(i)$表示$t$时刻$y_t=i$的情况，有：（其中$S$表示状态集合——$y$的所有情况）
$${\alpha }_t(i)=\sum _{j\in S}[{\phi }_t(y_{t-1}=j,y_t=i,X)\cdot {\alpha }_{t-1}(j)]$$
与此相同，我们可以发现${\Delta }_{right}$​可以写成：
$${\Delta }_{right}=\sum _{y_{t+1}}\left({\phi }_{t+1}(y_t=i,y_{t+1},X)\cdots \sum _{y_{T-1}}\left({\phi }_{T-1}(y_{T-2},y_{T-1},X)\sum _{y_T}{\phi }_T(y_{T-1},y_T,X)\right)\right)$$
和${\Delta }_{left}$相比，仅仅是反过来了而已，我们假设${\Delta }_{right}={\beta }_t(i)$表示$t$时刻$y_t=i$的情况，有：
$${\beta }_t(i)=\sum _{j\in S}[{\phi }_t(y_t=i,y_{t+1}=j,X)\cdot {\beta }_{t+1}(j)]$$
所以我们可以得到以下结论：
$$\{\begin{array}{l}P(y_t=i|X)=\frac{1}{Z}{\alpha }_t(i){\beta }_t(i)\\ {\alpha }_t(i)={\sum }_{j\in S}[{\phi }_t(y_{t-1}=j,y_t=i,X)\cdot {\alpha }_{t-1}(j)]\\ {\beta }_t(i)={\sum }_{j\in S}[{\phi }_t(y_t=i,y_{t+1}=j,X)\cdot {\beta }_{t+1}(j)]\end{array}$$

17.7 参数估计——Learning问题

Learning问题就是求解参数，原问题我们已经非常熟悉了：
$$\hat{\theta }=arg\max \prod _{i=1}^{N}P(y^{(i)},x^{(i)})$$
根据这道题的实际参数可以写为：
$$\{\begin{array}{l}\hat{\lambda },\hat{\eta }=arg{\max }_{\lambda ,\eta }{\prod }_{i=1}^{N}P(y^{(i)},x^{(i)})\\ P(Y|X)=\frac{1}{Z(x,\lambda ,\eta )}\exp {\sum }_{t=1}^T\left[{\lambda }^{T}f(y_{t-1},y_t,x_{1:T})+{\eta }^{T}g(y_t,x_{1:T})\right]\end{array}$$
由于问题中有连乘符号，所以我们改变一下形式：
$$\begin{array}{rl}\hat{\lambda },\hat{\eta }& =arg\underset{\lambda ,\eta }{\max }\prod _{i=1}^{N}P(Y^{(i)},X^{(i)})\\ & =arg\underset{\lambda ,\eta }{\max }\sum _{i=1}^N\log P(Y^{(i)},X^{(i)})\\ & =arg\underset{\lambda ,\eta }{\max }\sum _{i=1}^N\left(-\log Z(X^{(i)},\lambda ,\eta )+\sum _{t=1}^T\left[{\lambda }^{T}f(y_{t-1}^{(i)},y_t^{(i)},X^{(i)})+{\eta }^{T}g(y_t^{(i)},X^{(i)})\right]\right)\end{array}$$
最终可以写成：
$$\{\begin{array}{l}\hat{\theta }=arg{\max }_{\lambda ,\eta }\mathcal{L}(\lambda ,\eta ,X^{(i)})\\ \mathcal{L}(\lambda ,\eta ,X^{(i)})={\sum }_{i=1}^N\left(-\log Z(X^{(i)},\lambda ,\eta )+{\sum }_{t=1}^T\left[{\lambda }^{T}f(y_{t-1}^{(i)},y_t^{(i)},X^{(i)})+{\eta }^{T}g(y_t^{(i)},X^{(i)})\right]\right)\end{array}$$
既然方程已经出来了，我们就可以用很多种方式对参数进行求解了，本节中我们使用梯度上升的方法对其进行求解。

---

若要迭代求解参数，则需要分别求出参数${\nabla }_{\lambda }L$和${\nabla }_{\eta }L$（求偏导），确定梯度方向。以下由于上文公式对于两个参数对称，下文只求${\nabla }_{\lambda }L$作为样本。

首先化简${\nabla }_{\lambda }L$​：
$${\nabla }_{\lambda }\mathcal{L}=\sum _{i=1}^N\left(\sum _{t=1}^{T}f(y_{t-1}^{(i)},y_t^{(i)},X^{(i)})-{\nabla }_{\lambda }\log Z(X^{(i)},\lambda ,\eta )\right)$$
根据化简后的公式，我们知道只要能求出${\nabla }_{\lambda }\log Z(X^{(i)},\lambda ,\eta )$，就能知道梯度方向了。这里我们发现，$\log Z(X^{(i)},\lambda ,\eta )$实际上是对数配分函数(log partition function)。在指数族分布的8.2中我们证明过对数配分函数的导数是其分布的期望。

所以公式可以写为：
$$\begin{array}{rl}& {\nabla }_{\lambda }\log Z(X^{(i)},\lambda ,\eta )\\ =& E_{Y|X^{(i)}}[f(y_{t-1},y_t,X^{(i)})]\\ =& \sum _Y\left[P(Y|X^{(i)})\cdot \sum _{t=1}^{T}f(y_{t-1},y_t,X^{(i)})\right]\\ =& \sum _{t=1}^T\sum _Y\left[P(Y|X^{(i)})\cdot f(y_{t-1},y_t,X^{(i)})\right]\\ =& \sum _{t=1}^T\sum _{y_1,\dots ,y_{t-2}}\sum _{y_{t-1}}\sum _{y_t}\sum _{y_{t+1},\dots ,y_T}\left[P(Y|X^{(i)})\cdot f(y_{t-1},y_t,X^{(i)})\right]\\ =& \sum _{t=1}^T\sum _{y_{t-1}}\sum _{y_t}\left[\left(\sum _{y_1,\dots ,y_{t-2}}\sum _{y_{t+1},\dots ,y_T}P(Y|X^{(i)})\right)\cdot f(y_{t-1},y_t,X^{(i)})\right]\\ =& \sum _{t=1}^T\sum _{y_{t-1}}\sum _{y_t}\left[P(y_{t-1},y_t|X^{(i)})\cdot f(y_{t-1},y_t,X^{(i)})\right]\end{array}$$
化简到这一步我们就发现，$P(y_{t-1},y_t|X^{(i)})$​和17.6中的求边缘概率相同，用相同方法可以求出其结果，所以梯度方向就可以得到为：
$${\nabla }_{\lambda }\mathcal{L}=\sum _{i=1}^N\sum _{t=1}^T\left[f(y_{t-1}^{(i)},y_t^{(i)},X^{(i)})-\sum _{y_{t-1}}\sum _{y_t}\left(P(y_{t-1},y_t|X^{(i)})\cdot f(y_{t-1},y_t,X^{(i)})\right)\right]$$
若采用梯度上升法，迭代公式就是：
$$\{\begin{array}{l}{\lambda }^{(t+1)}={\lambda }^{(t)}+step\cdot {\nabla }_{\lambda }\mathcal{L}({\lambda }^{(t)},{\eta }^{(t)})\\ {\eta }^{(t+1)}={\eta }^{(t)}+step\cdot {\nabla }_{\eta }\mathcal{L}({\lambda }^{(t)},{\eta }^{(t)})\end{array}$$
但实际过程中，使用梯度上升的收敛速度比较慢，会采用别的方法。