Linear Regression -- 线性回归

机器学习

"Fiele of study that gives computers the ability to learn withouut being explicity programmed." -- Arthur Samuel (1959)

机器学习分为两大类，一类是监督学习（supervised learning），一类是非监督学习（unsurpervised learning）。监督学习中又有常见的两大类，一类是回归（regression），一类是分类（classification）。

简单来说，监督学习就是给机器学习的训练集有标注（label），告诉机器什么是“正确的”；而非监督学习就是只提供数据集，让机器自己试图找出数据集的某些“结构”。

举个例子，假如你要对某地的房价进行预测，首先你告诉机器之前的房子信息（大小，房间数，年龄...）和相应的房价，然后让机器学习房价和房子信息之间的相关参数，再用这些参数（模型）去对新的房价进行预测。在这个过程中，你提供给机器的数据称为训练集（training set），机器学习到的参数集合称为模型（model），最终预测的房价称为测试集（test set），预测的准确与否可以作为性能度量（performance）。此外，由于该例子中，我们在训练集给出了相对于的房价（“right answer" or "label"），所以这种机器学习被称为监督学习。

还有一个监督学习的例子，假如你要根据肿瘤的大小预测肿瘤的良性还是恶性（benign or malignant），在训练集中，你对不同大小的肿瘤进行标记，通过模型训练后，拿来预测新的肿瘤是否为恶性肿瘤。这也是监督学习的例子，不同于上一个例子用来预测数据（regression），这个例子是用来分类（classification）。到这，我们可以总结，监督学习的关键在于标记（label），就好像我们人为给机器加了一些限定和法则，告诉机器具体的数据大小和种类有那些（理解监督学习的含义）。

非监督学习举例，延续上个例子，假如我们没有给训练集进行标记，而是告诉机器，我有这些数据（不同肿瘤的大小，生长年龄），然后让机器试图对这些数据进行分类，如果数据结构比较明显，机器也许能分出两大类，告诉我们，这些数据可能代表着两种不同的东西。

日常生活中，非监督学习的应用有很多，例如：Google news，DNA microarray，Grouping customes... 这些都属于非监督学习的聚类（Clustering）。还有其他类型，如：异常检测（Anomaly detection），数据降维（Dimensionality reduction）...

线性回归 (Linear regression)

在上面我们举了房价预测的例子，这就是一种线性回归的例子。我们想通过寻找其他房子的房子信息与房价之间的关系，来对新的房价进行预测。

首先，我们要对问题抽象出相应的符合表示（Notation）。

xj: 代表第j个特征 x(i)：代表第i个样本

x(i) j：代表第i个样本的第j个特征 y(i)：代表第i个样本的标记（房价）

wj：第j个特征的系数 b：系数常量

线性模型：f(x) = w1 * x1 + w2 * x2 + ... + wn * xn + b

向量化（vectorization）： $f(x) = w \cdot x + b$

（向量化能简化公式表示，更重要的是，有numpy库的支持，向量化表示能大大减少代码量和计算时间）代码如下：

import numpy as np
w = np.array([w1, w2, w3])
b = 4
x = np.array([x1, x2, x3])
f = np.dot(w, x) + b

代价函数（Cost Function）

接着，我们要定义代价函数（cost function）也叫损失函数（loss function）

什么是代价函数？

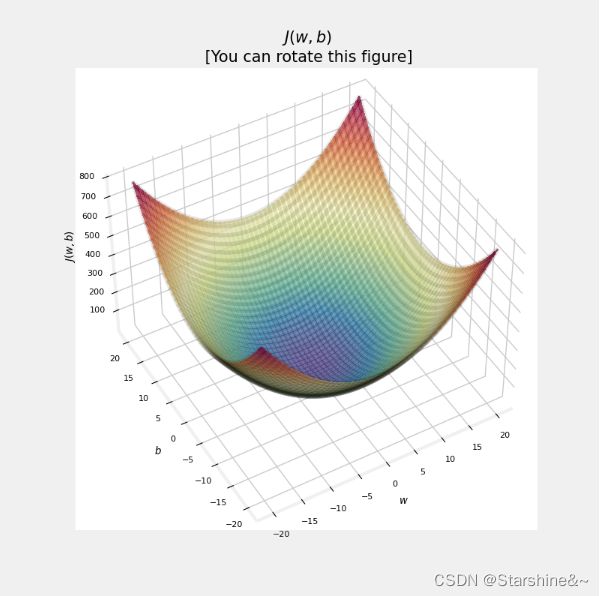
代价函数是用来衡量模型预测与真实值之间的差距，对于多个样本而言，我们可以通过求平均值来衡量模型预测与真实值之间的平均差距J(θ)，进而评价模型的好坏。在训练模型的过程中，我们就是想让机器通过不断的调整参数，来使用定义好的代价函数不断下降，当我们取到minJ(θ)最小值的时候，我们就得到了最完美的参数。

代价函数定义：

$J(\Theta ) = \frac{1}{2m}\sum_{i=1}^{m}(f(x^{(i)}) - y^{(i)})^{2}$

这里，我们用了均方误差（Mean squared error）函数来定义代价函数。系数2m是为了方便后面求导时多出来的2进行约分。均分误差有个很好的特点，那就是几何上函数都是碗状形（bow-shape），这种良好的形状保证我们只有一个最优解。事实上，函数可能有很多的局部最小值（local mininum），这种情况可能让我们通过梯度下降（gradient descent）训练出来的模型并不是最优解。而在本例中，我们将不用考虑这种情况！

def compute_cost(x, y, w, b): 
    """
    Computes the cost function for linear regression.
    
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    
    Returns
        total_cost (float): The cost of using w,b as the parameters for linear regression
               to fit the data points in x and y
    """
    # number of training examples
    m = x.shape[0] 
    
    cost_sum = 0 
    for i in range(m): 
        f_wb = w * x[i] + b   
        cost = (f_wb - y[i]) ** 2  
        cost_sum = cost_sum + cost  
    total_cost = (1 / (2 * m)) * cost_sum  

    return total_cost

（注：x.shape[0] 得到 x 矩阵的行数，关于numpy的用法可以参考What is NumPy? — NumPy v1.24 Manual）

梯度下降 (Gradient descent)

寻找最优解 —— 梯度下降（gradient descent）

方法概述：

1. 从最开始定义的参数 w，b 开始

2. 通过梯度下降不断改变参数来减少代价函数

3. 直到我们到达最小值或接近最小值时停止

Gradient descent:

repeat {

$w_{j} = w_{j} - \alpha \frac{\partial J(w,b)}{\partial w_{j}} = w_{j} - \alpha \frac{1}{m} \sum_{i=1}^{m}(f(x^{(i)}) - y^{(i)}) \cdot x_{j}^{(i)}$

$b = b - \alpha\frac{\partial J(w,b)}{\partial b} = b - \alpha \frac{1}{m} \sum_{i=1}^{m}(f(x^{(i)}) - y^{(i)})$

（simultaneously update w and b）

} until convergence

注意在调整参数时，w和b要同时调整，也就是说不能用调整好w的函数代入b的更新数中，两者应该使用同样的f(x)

def compute_gradient(x, y, w, b): 
    """
    Computes the gradient for linear regression 
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    Returns
      dj_dw (scalar): The gradient of the cost w.r.t. the parameters w
      dj_db (scalar): The gradient of the cost w.r.t. the parameter b     
     """
    
    # Number of training examples
    m = x.shape[0]    
    dj_dw = 0
    dj_db = 0
    
    for i in range(m):  
        f_wb = w * x[i] + b 
        dj_dw_i = (f_wb - y[i]) * x[i] 
        dj_db_i = f_wb - y[i] 
        dj_db += dj_db_i
        dj_dw += dj_dw_i 
    dj_dw = dj_dw / m 
    dj_db = dj_db / m 
        
    return dj_dw, dj_db

def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function): 
    """
    Performs gradient descent to fit w,b. Updates w,b by taking 
    num_iters gradient steps with learning rate alpha
    
    Args:
      x (ndarray (m,))  : Data, m examples 
      y (ndarray (m,))  : target values
      w_in,b_in (scalar): initial values of model parameters  
      alpha (float):     Learning rate
      num_iters (int):   number of iterations to run gradient descent
      cost_function:     function to call to produce cost
      gradient_function: function to call to produce gradient
      
    Returns:
      w (scalar): Updated value of parameter after running gradient descent
      b (scalar): Updated value of parameter after running gradient descent
      J_history (List): History of cost values
      p_history (list): History of parameters [w,b] 
      """
    
    w = copy.deepcopy(w_in) # avoid modifying global w_in
    # An array to store cost J and w's at each iteration primarily for graphing later
    J_history = []
    p_history = []
    b = b_in
    w = w_in
    
    for i in range(num_iters):
        # Calculate the gradient and update the parameters using gradient_function
        dj_dw, dj_db = gradient_function(x, y, w , b)     

        # Update Parameters using equation (3) above
        b = b - alpha * dj_db                            
        w = w - alpha * dj_dw                            

        # Save cost J at each iteration
        if i<100000:      # prevent resource exhaustion 
            J_history.append( cost_function(x, y, w , b))
            p_history.append([w,b])
        # Print cost every at intervals 10 times or as many iterations if < 10
        if i% math.ceil(num_iters/10) == 0:
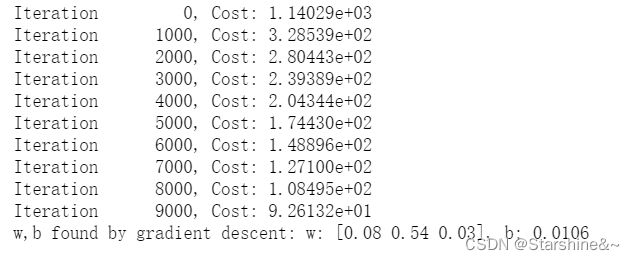
            print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",
                  f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e}  ",
                  f"w: {w: 0.3e}, b:{b: 0.5e}")
 
    return w, b, J_history, p_history #return w and J,w history for graphing

学习率α (learning rate)

在梯度下降算法中，有一个参数α，我们称为学习率。学习率，顾名思义，就是学习的效率。那么，学习率是否越大越好呢？

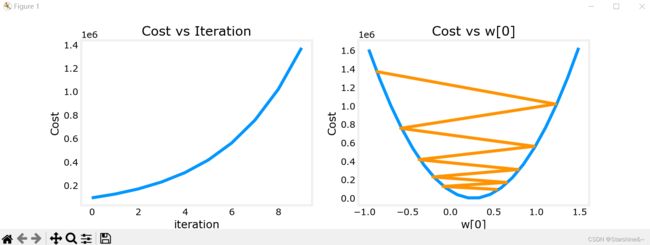
通过将梯度下降过程图像化，我们可以发现，如果学习率过大，代价函数反而不降反升！So bad!

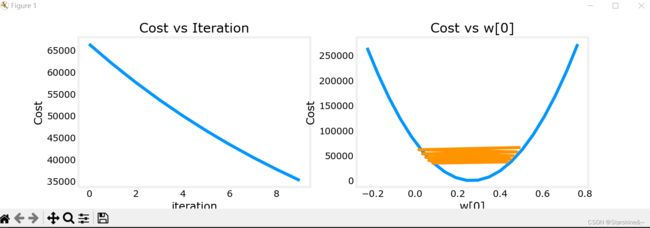
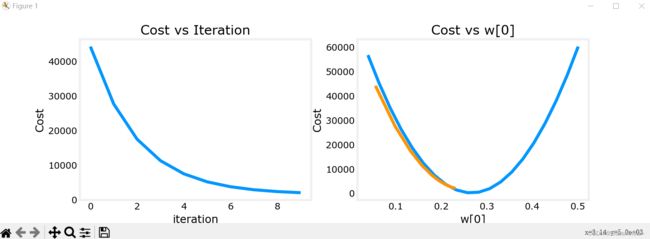
什么原因导致这种情况的发生呢？观察代价函数图像，我们可以看出，如果参数w从右侧出发，导数小于0，代入梯度下降公式会使w增加，向右前进（图三）；反之亦然（vice versa）。但如果学习率过大，每次跨的距离过大（big step），就会错过最小值的点，甚至导致函数不收敛（如图一）。如果学习率过小（baby step），则每次跨的距离太小，导致算法速度过慢，迭代次数过多。

图一

图二

图三

代码如下：

import numpy as np
import matplotlib.pyplot as plt
from lab_utils_multi import  load_house_data, run_gradient_descent 
from lab_utils_multi import  norm_plot, plt_equal_scale, plot_cost_i_w
from lab_utils_common import dlc
np.set_printoptions(precision=2)
plt.style.use('deeplearning.mplstyle')

# load the dataset
X_train, y_train = load_house_data()
X_features = ['size(sqft)','bedrooms','floors','age']

fig,ax=plt.subplots(1, 4, figsize=(12, 3), sharey=True)
for i in range(len(ax)):
    ax[i].scatter(X_train[:,i],y_train)
    ax[i].set_xlabel(X_features[i])
ax[0].set_ylabel("Price (1000's)")
plt.show()

#set alpha to 9.9e-7
_, _, hist = run_gradient_descent(X_train, y_train, 10, alpha = 9.9e-7)
plot_cost_i_w(X_train, y_train, hist)

#set alpha to 9e-7
_, _, hist = run_gradient_descent(X_train, y_train, 10, alpha = 9e-7)
plot_cost_i_w(X_train, y_train, hist)

#set alpha to 1e-7
_, _, hist = run_gradient_descent(X_train, y_train, 10, alpha = 1e-7)
plot_cost_i_w(X_train, y_train, hist)

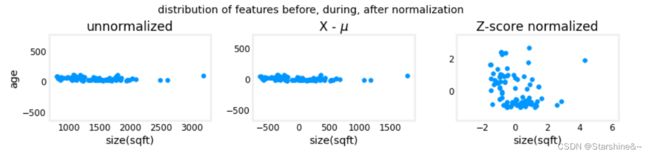
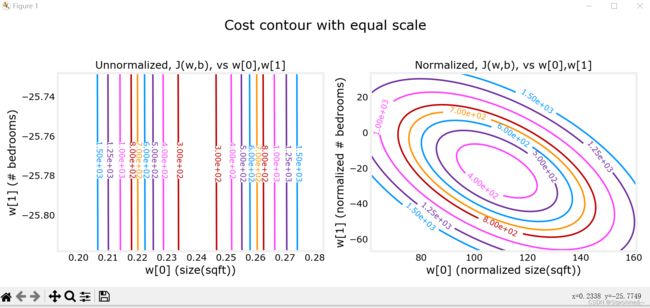
特征缩放（feature scaling)

回到主题 —— 房价预测，我们提供房子的信息包括房子大小（size），使用年龄（age）等等，这些特征的取值范围不同，数量级也不同。数据本身带有量纲，范围变化也大小不一，可能导致图像化时表现为拥挤，系数数量级差过大等等。总之，使用原始数据会导致种种的不变，因此，我们要对其进行特征缩放，让不同特征数量级相对接近。

特征放缩有几种常见的方法：

1. Mean normalization（均值归一法）

$x = \frac{x-\mu }{max-min}$

max, min: x 取值的最大值和最小值

2. Z-score normalization

$x = \frac{x-\mu }{\sigma }$

这些方法都试图将数据集中（close -1 - 1），将平均值取为0，缩小数据范围。

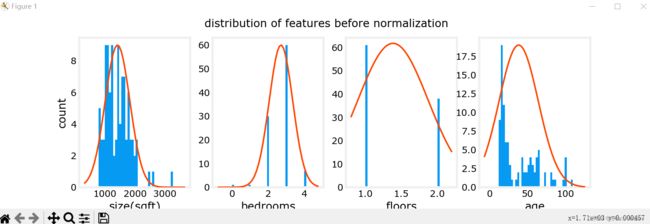
before feature scaling

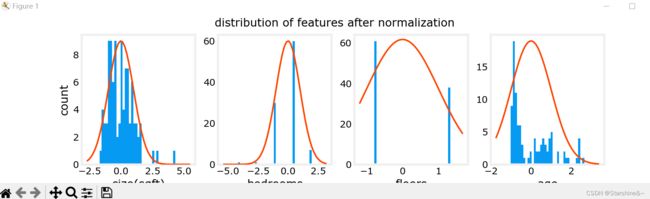
after feature scaling

def zscore_normalize_features(X):
    """
    computes  X, zcore normalized by column

    Args:
      X (ndarray (m,n))     : input data, m examples, n features

    Returns:
      X_norm (ndarray (m,n)): input normalized by column
      mu (ndarray (n,))     : mean of each feature
      sigma (ndarray (n,))  : standard deviation of each feature
    """
    # find the mean of each column/feature
    mu = np.mean(X, axis=0)  # mu will have shape (n,)
    # find the standard deviation of each column/feature
    sigma = np.std(X, axis=0)  # sigma will have shape (n,)
    # element-wise, subtract mu for that column from each example, divide by std for that column
    X_norm = (X - mu) / sigma

    return (X_norm, mu, sigma)

特征工程（feature engineer)

上面我们提到的都是线性回归（linear regression），然而，在现实生活中，模型不都是线性关系的。就如房价和年龄不一定符合线性关系，有可能是平方关系。此外，不同特征之间的关系可能对结果造成影响。

举个例子，假如我们现在预测一块地皮的价格，价格可能和长度（x1)有关，可能和宽度(x2)有关，你可能会对这两个特征进行提取预测。然而，事实上，地皮的价格还跟面积有关（x1*x2），并且通常情况下，我们就是根据面积在计算地皮价格。x1 * x2 就是我们根据 x1 和 x2 两个特征新创造出来的特征，注意，这将导致我们的模型不在是线性的。

特征选择

对于原有的特征x1，x2，我们能创造出很多新的特征：x1**2，x2**2，x1**3，x1*x2 ...

如何选择呢？我们从一个简单例子讲起：=1+2

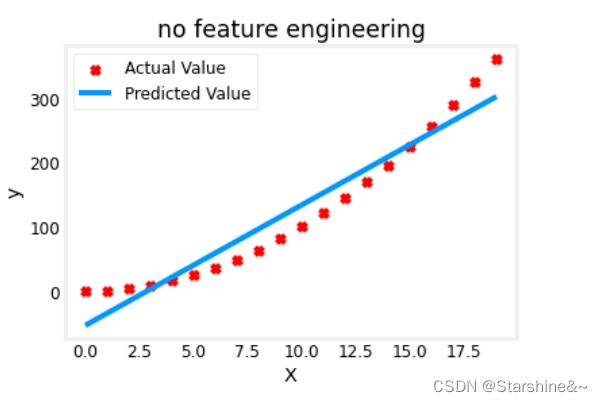
假如真实模型是二次关系，而我们依旧选择线性关系模型来预测（f(x) = wx + b）：

可以看到，线性模型来预测二次关系并不是很理想。

# create target data
x = np.arange(0, 20, 1)
y = 1 + x**2
X = x.reshape(-1, 1)

model_w,model_b = run_gradient_descent_feng(X,y,iterations=1000, alpha = 1e-2)

plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("no feature engineering")
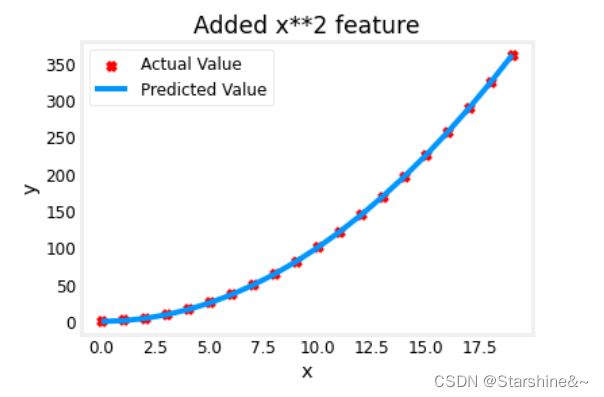
plt.plot(x,X@model_w + model_b, label="Predicted Value");  plt.xlabel("X"); plt.ylabel("y"); plt.legend(); plt.show()

如果我们使用二次模型，将会很好地符合数据（f(x) = w * x**2 + b）：

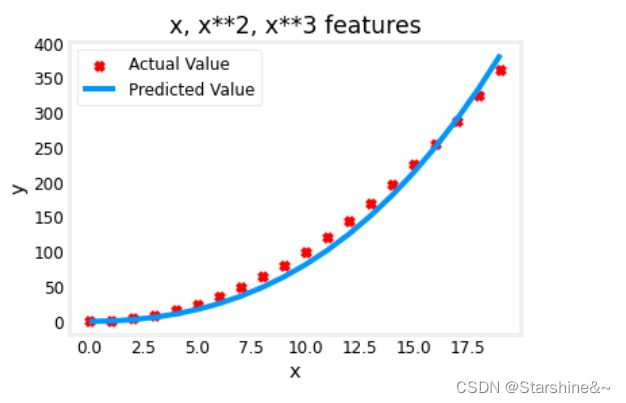
如果我们选择三次模型呢（f(x) = w1 * x + w2 * x**2 + w3 * x**3 + b）：

# create target data
x = np.arange(0, 20, 1)
y = x**2

# engineer features .
X = np.c_[x, x**2, x**3]   #<-- added engineered feature

model_w,model_b = run_gradient_descent_feng(X, y, iterations=10000, alpha=1e-7)

plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("x, x**2, x**3 features")
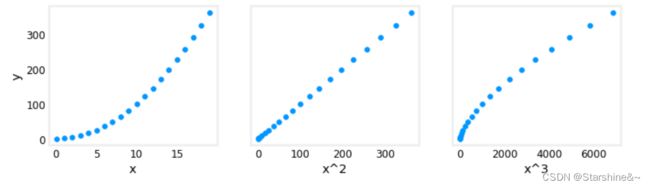
plt.plot(x, X@model_w + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()

观察数据，我们可以看到，w1，w3都比较小，接近0；也就是说，在梯度下降的过程中，我们找到了数据的某些特征，它和二次型比较接近，而与线性和三次型相关性比较低。也就是说，这个数据很可能是平方相关的。

Gradient descent is picking the 'correct' features for us by emphasizing its associated parameter

从另一个角度看，只有x**2这个特征和y是线性相关的，也就是说，我们用x**2作为特征，依然可以运用线性回归进行预测。

# create target data
x = np.arange(0, 20, 1)
y = x**2

# engineer features .
X = np.c_[x, x**2, x**3]   #<-- added engineered feature
X_features = ['x','x^2','x^3']

fig,ax=plt.subplots(1, 3, figsize=(12, 3), sharey=True)
for i in range(len(ax)):
    ax[i].scatter(X[:,i],y)
    ax[i].set_xlabel(X_features[i])
ax[0].set_ylabel("y")
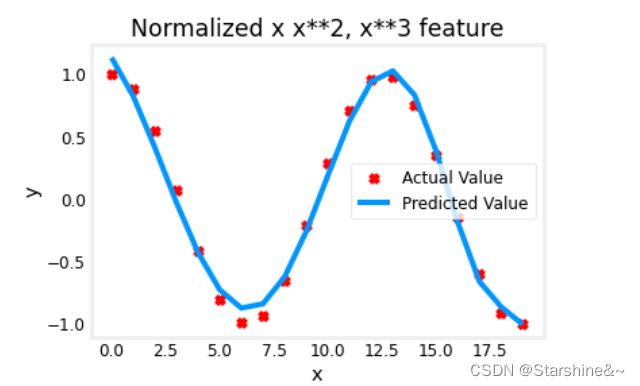
plt.show()

对于一些复杂的函数，如：y = cos(x/2)，我们依旧可以用特征工程来模拟，使用梯度下降会为我们自动选择合适的特征工程，增大它的相关系数，减小相关性较小的特征系数。观察结果系数值，我们也可以人为为模型选择合适的特征再进行模拟。

x = np.arange(0,20,1)
y = np.cos(x/2)

X = np.c_[x, x**2, x**3,x**4, x**5, x**6, x**7, x**8, x**9, x**10, x**11, x**12, x**13]
X = zscore_normalize_features(X) 

model_w,model_b = run_gradient_descent_feng(X, y, iterations=1000000, alpha = 1e-1)

plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("Normalized x x**2, x**3 feature")
plt.plot(x,X@model_w + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()

Scikit-learn

接下来，我们将学习一个能实现我们所学内容的库。

sklearn.linear_model 是 scikit-learn 库中用于线性回归分析的模块。它包含了许多线性回归的模型，如线性回归，岭回归，Lasso 回归等。

SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型；LinearRegression类则通过正规方程优化。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler
from lab_utils_multi import  load_house_data
from lab_utils_common import dlc
np.set_printoptions(precision=2)
plt.style.use('deeplearning.mplstyle')

梯度下降（Gradient descent)

#Load the data set
X_train, y_train = load_house_data()
X_features = ['size(sqft)','bedrooms','floors','age']

#Scale/normalize the training data
scaler = StandardScaler()
X_norm = scaler.fit_transform(X_train)
print(f"Peak to Peak range by column in Raw        X:{np.ptp(X_train,axis=0)}")   
print(f"Peak to Peak range by column in Normalized X:{np.ptp(X_norm,axis=0)}")

#Create and fit the regression model
sgdr = SGDRegressor(max_iter=1000)
sgdr.fit(X_norm, y_train)
print(sgdr)
print(f"number of iterations completed: {sgdr.n_iter_}, number of weight updates: {sgdr.t_}")

#View parameters
b_norm = sgdr.intercept_
w_norm = sgdr.coef_
print(f"model parameters:                   w: {w_norm}, b:{b_norm}")
print( "model parameters from previous lab: w: [110.56 -21.27 -32.71 -37.97], b: 363.16")

# make a prediction using sgdr.predict()
y_pred_sgd = sgdr.predict(X_norm)
# make a prediction using w,b. 
y_pred = np.dot(X_norm, w_norm) + b_norm  
print(f"prediction using np.dot() and sgdr.predict match: {(y_pred == y_pred_sgd).all()}")

#Make predictions
print(f"Prediction on training set:\n{y_pred[:4]}" )
print(f"Target values \n{y_train[:4]}")

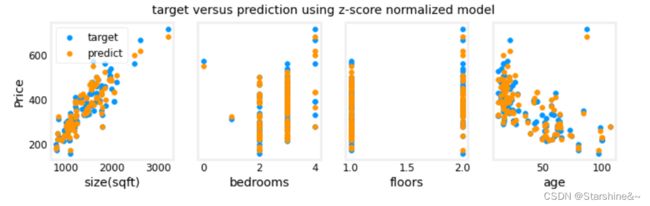
# plot predictions and targets vs original features    
fig,ax=plt.subplots(1,4,figsize=(12,3),sharey=True)
for i in range(len(ax)):
    ax[i].scatter(X_train[:,i],y_train, label = 'target')
    ax[i].set_xlabel(X_features[i])
    ax[i].scatter(X_train[:,i],y_pred,color=dlc["dlorange"], label = 'predict')
ax[0].set_ylabel("Price"); ax[0].legend();
fig.suptitle("target versus prediction using z-score normalized model")
plt.show()

Linear Regression, closed-form solution：