图像降噪网络：KBNet 论文笔记

0 前言

Zhang Y, Li D, Shi X, et al. KBNet: Kernel Basis Network for Image Restoration[J]. arXiv preprint arXiv:2303.02881, 2023.
https://arxiv.org/abs/2303.02881

论文主要提出了 Kernel Basis Attention Module 注意力模块，称为 KBA 模块。该模块可以轻松嵌入到现有的网络架构如 UNet 当中，且相比于 Transformer 等注意力机制具有更低的复杂度，但能够却在包括降噪、去模糊等多个底层图像重建任务中取得了 SOTA 的成绩。关于真实噪声图像降噪的实验结果对比如下：

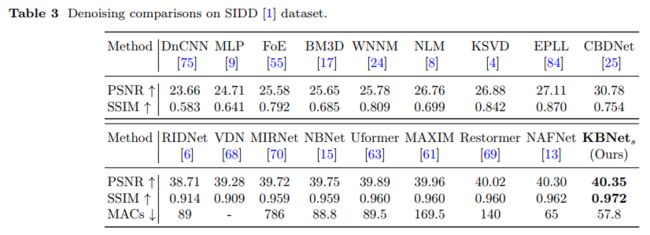
1 相关工作与动机

虽然基于 Scaled Dot-Product Attention 注意力机制的 Transformer 模型在自然语言处理领域取得了非常优异的成绩，但在图像处理特别是图像质量重建领域却存在一些水土不服的问题。相比于抽象而简短的文字，图像所包含的信息是极其稀疏的，一张图片动辄包含数以万计的像素，因此简单地应用 Transformer 模型需要极大的算力代价。为此，一些基于局部窗口的 Transformer 模型相继被提出。例如在 Wang 等人提出的 Uformer (arxiv:2106.03106) 模型中，作者提出了基于不重叠的固定尺寸窗口的 Transformer 模块，极大地降低了注意力机制所需的复杂度；又因为该 Transformer 模块所用窗口尺寸是固定的，而图像处理领域通常基于 UNet 架构，随着网络深度的增加，特征尺寸会因为下采样而不断地缩小，最终的窗口即有可能包含整个特征，从而实现全局的注意力机制，弥补不重叠窗口所带来的局部性问题。

然而，Transformer 模型应用于图像重建任务的问题并不局限于上述的计算复杂度。在图像中，像素的局部相似性远高于相邻的文字，相邻的像素往往具有几乎相同的像素值；同时，图像在非局部区域也存在着大量的自相似性，即同一种纹理结构，往往可能重复地出现在图像的不同位置。对于 Scaled Dot-Product Attention 注意力机制，其结构如下图所示：

图 1 Scaled Dot-Product Attention Module

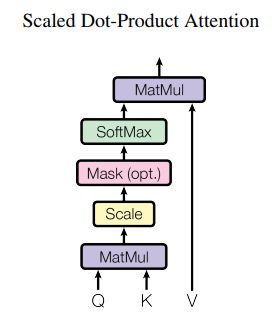
其中 $\mathbf{Q},\mathbf{K},\mathbf{V}\in {\mathbb{R}}^{N\times C}$，三者在图像处理中通常是相同的，$N$ 为特征的像素个数，即 $H\times W$，$C$ 即为特征的通道数。那么注意力机制可表示为

$$\text{Attention}\left(\mathbf{Q},\mathbf{K},\mathbf{V}\right)=\text{softmax}\left(\frac{\mathbf{Q}{\mathbf{K}}^T}{scale}\right)\mathbf{V}.$$

在这里，$\mathbf{Q}{\mathbf{K}}^T$ 本质上就是计算特征中每个像素与其他像素的相关性，并通过 softmax 操作转换为与其他像素的叠加权重，最终通过乘以 $\mathbf{V}$ 获得其他像素的加权叠加结果，并以此作为新的特征像素。相比于卷积操作，这种注意力机制虽然获得了更大的特征可视域与像素自适应性，但缺点也是明显的。首先，它忽视了图像像素的局部相似性，将太多的计算花费在了远离当前像素的区域，而这并不能保证相匹配的收益；再者，它只是在单个像素上计算相关性，这很难捕捉图像中广泛存在的自相似结构，而更容易受到噪声的影响。

以上的问题，恰好是卷积操作所擅长解决的。因为卷积核通常很小，所以卷积只会局限于局部的像素叠加，不会造成太大的算力浪费；同时，卷积具有平移不变性，并可通过卷积核来学习与识别图像中存在的各种纹理结构，如条纹、分叉等等。我们把这种局部性与平移不变性称为卷积操作的归纳偏置 (Inductive Biases)，而这种归纳偏置又与图像的特性非常切合，这也是为什么 CNN 能够在图像处理领域大放异彩的重要原因。然而，我们也不能否认，CNN 具有较差的像素自适应性，即我们总是使用相同的卷积核来处理不同的像素。由于图像结构可能存在着任意的旋转与透视形变等等，这是卷积所不擅长处理的，单纯通过增加卷积核的个数并不能很好地解决这些问题。

基于以上的讨论，论文尝试综合卷积的归纳偏置与注意力机制的像素自适应性，提出了 Kernel Basis Attention Module 注意力模块。

2 KBA Module

KBA 模块的结构如图 2 所示。这里会结合作者所开源代码 (https://github.com/zhangyi-3/KBNet) 进行各部分的解析。

图 2 Kernel Basis Attention Module

对于输入特征 $\mathbf{X}\in {\mathbb{R}}^{H\times W\times C}$，我们希望学习 $N$ 个卷积核 $\mathbf{W}=\left\{{\mathbf{W}}_1,{\mathbf{W}}_2,...,{\mathbf{W}}_N\right\}$，其中 ${\mathbf{W}}_i\in {\mathbb{R}}^{K\times K\times C\times C}$，也就是普通 CNN 网络中的卷积核，通常 $K=3$。实际上，为了降低参数的数量，这里的卷积通常使用 GroupConv2D。记 Group 的个数为 $G$，每个 Group 的通道数为 $Gc$，其中 $C=G\times Gc$，那么有 ${\mathbf{W}}_i\in {\mathbb{R}}^{K\times K\times Gc\times Gc\times G}$。论文中取 $Gc=4$。除了卷积核以外，在具体的实现中，通常还会包含卷积后的偏置量的学习。关于卷积核与偏置的代码定义如下：

nset=32, k=3, gc=4
g = c // gc
w = nn.Parameter(torch.zeros(1, nset, c * c // g * k ** 2))
b = nn.Parameter(torch.zeros(1, nset, c))

注意这 $N$ 个卷积核是由所有像素共享的，但是我们并不直接使用这些卷积核进行 $N$ 次卷积运算。为了实现各个像素的自适应性，我们基于输入特征 $\mathbf{X}\in {\mathbb{R}}^{H\times W\times C}$，学习到每个像素关于这 $N$ 个卷积核的融合权重，称为 Fusion Coefficient Map，以 $\mathbf{F}\in {\mathbb{R}}^{H\times W\times N}$ 记之。那么，每个像素实际所用的卷积核为前述 $N$ 个卷积核的加权叠加，即

$${\mathbf{M}}_{i,j}=\sum _{n=1}^N{F}_{i,j,n}{\mathbf{W}}_n$$

基于这种方法，我们可以综合不同卷积核的特性。例如，一个斜线方向的纹理可以近似分解为若干个水平与垂直方向纹理的组合。虽然我们可以通过增加卷积核的数量来捕捉不同方向的斜线纹理，但由于其角度是任意，我们并不能定义无限数量的卷积核。而通过卷积核的加权融合方法，我们只需学习关于少量水平与垂直纹理的卷积核的融合权重，就能获得适用于任意角度斜线纹理的卷积核。对于其他情况同理。通过这种自适应卷积核融合的方法，我们弥补了普通卷积运算对于旋转与透视等变换敏感的缺陷，强化了卷积对于图像结构自相似性的归纳偏置能力。由于每个像素最终只会进行一次卷积，所以其计算复杂度并不会因为共享卷积核数量 $N$ 的增加而增长太多。

关于融合权重 $\mathbf{F}$ 的计算，论文并不使用 Transformer 等复杂的模型，而仅使用比较简单的卷积运算。这部分的代码如下。作者使用了两个分支，一个大致为 3x3 的可分离卷积，另一个为 1x1 的通道间变换，最终通过一个可学习的叠加权重 attgamma 进行融合。尽管 Transformer 模型的注意力机制通过 softmax 将 $\mathbf{Q}{\mathbf{K}}^T$ 进行归一化，作者发现对于 $\mathbf{F}$ 的归一化是不必要的，因为 softmax 会把过多的权重分配到更大的数值上，从而降低了卷积核融合的效果。因此，$\mathbf{F}$ 的计算量是非常小的。因为 $\mathbf{F}$ 的计算只涉及到 3x3 的可视域，所以 $\mathbf{F}$ 更多关注的是当前像素局部邻域的信息，关于全局的自相似性则是通过共享的 $N$ 个卷积核 $\mathbf{W}$ 来实现的。而随着 UNet 深度的增加，特征尺寸越来越小，$\mathbf{F}$ 对于局部信息综合的能力也会越来越强。基于这种对共享卷积核进行自适应融合的方法，我们一方面保留了卷积运算的归纳偏置，又实现了各个像素的自适应性。

''' simplified GLU function
'''
class SimpleGate(nn.Module):
    def forward(self, x):
        x1, x2 = x.chunk(2, dim=1)
        return x1 * x2

''' Fusion Feature Map1
spatial and channel attention
input: CxHxW -> F1: NxHxW
'''
interc = min(c, 32)     # c must be divisible by 32 if c > 32
self.conv2 = nn.Sequential(
    nn.Conv2d(in_channels=c, out_channels=interc, kernel_size=3, padding=1, stride=1, groups=interc, bias=True),
    SimpleGate(),   # this would half the channel
    nn.Conv2d(interc // 2, self.nset, 1, padding=0, stride=1),
)

''' Fusion Feature Map2
1x1 conv, channel attention
input: CxHxW -> F2: NxHxW
'''
self.conv211 = nn.Conv2d(in_channels=c, out_channels=self.nset, kernel_size=1)

'''F = F1 * attgamma + F2
'''
self.attgamma = nn.Parameter(torch.zeros((1, self.nset, 1, 1)) + 1e-2, requires_grad=True)
att = self.conv2(x) * self.attgamma + self.conv211(x)

当为输入特征 $\mathbf{X}\in {\mathbb{R}}^{H\times W\times C}$ 每个像素都获得一个自适应的卷积核 ${\mathbf{M}}_{i,j}\in {\mathbb{R}}^{K\times K\times Gc\times Gc\times G}$ 后，我们就可以对输入特征进行自适应的卷积。为了更好地捕捉局部信息，作者首先对输入特征基于简单的卷积运算进行增强，获得 Enhanced Feature Map，记为 ${\mathbf{X}}_e\in {\mathbb{R}}^{H\times W\times C}$，然后在 ${\mathbf{X}}_e$ 上进行自适应的卷积运算。这部分代码如下：

''' Enhanced Feature Map
1. 1x1 convolution
2. 3x3 grouping convolution, groups=c, i.e. depthwise
input: CxHxW -> Xe: CxHxW
'''
self.conv1 = nn.Conv2d(in_channels=c, out_channels=c, kernel_size=1, padding=0, stride=1, groups=1, bias=True)
self.conv21 = nn.Conv2d(in_channels=c, out_channels=c, kernel_size=3, padding=1, stride=1, groups=c, bias=True)
x = self.conv21(self.conv1(x))

''' F: (HW) x N
bias: [(HW) x N] .dot (N x C) -> (HW) x C
attk: [(HW) x N] .dot (N x C x [GC x K x K]) -> (HW) x C x [GC x K x K]
'''
att  = att.reshape(B, nset, H * W).transpose(-2, -1)
bias = att @ selfb  
attk = att @ selfw

''' unfold the group conv2D to matmul
'''
uf = torch.nn.functional.unfold(x, kernel_size=selfk, padding=selfk // 2)
# for unfold att / less memory cost
uf = uf.reshape(B, selfg, selfc // selfg * KK, H * W).permute(0, 3, 1, 2)
attk = attk.reshape(B, H * W, selfg, selfc // selfg, selfc // selfg * KK)
# uf: (HW) x G x (GC x K x K)
# attk: (HW) x G x GC x (GC x K X K)
x = attk @ uf.unsqueeze(-1)
x = x.squeeze(-1).reshape(B, H * W, selfc) + bias
x = x.transpose(-1, -2).reshape(B, selfc, H, W)

3 MFF Block

为了综合输入特征多方面的信息，作者在 KBA 模块的基础上拓展出了 Multi-axis Feature Fusion Block，其结构如下所示。

图 3 Multi-axis Feature Fusion Block

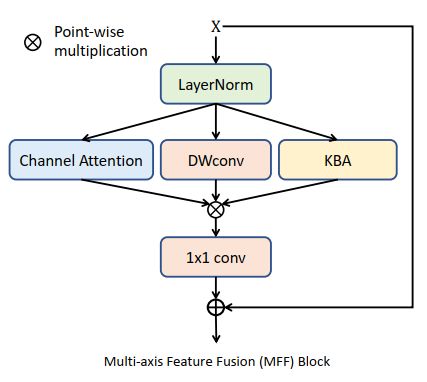
类似于 Transformer 模型，MFF 首先对输入特征进行 LayerNorm。LN 层在 Transformer 等 NLP 模型中主要是为了解决 Batch 太小，不方便进行 BatchNorm 标准化的问题。由于 BN 层在样本间进行标准化，引入其他的样本可能会造成当前样本纹理等信息发生剧烈变化，不利于后续样本的重建，所以在底层图像重建如降噪等任务中通常都被移除了。而 LN 只在各个样本的特征通道上独立进行标准化，不会对特征纹理造成太大的影响，所以 LN 作为一种标准化方法重新被图像重建任务所采纳，以保证模型优化的稳定性。关于 LN 层的定义如下：

self.register_parameter('weight', nn.Parameter(torch.ones(channels), requires_grad=requires_grad))
self.register_parameter('bias', nn.Parameter(torch.zeros(channels), requires_grad=requires_grad))
self.eps = 1e-6
def LayNorm(x, weight, bias, eps):
    N, C, H, W = x.size()
    mu = x.mean(1, keepdim=True)
    var = (x - mu).pow(2).mean(1, keepdim=True)
    y = (x - mu) / (var + eps).sqrt()
    y = weight.view(1, C, 1, 1) * y + bias.view(1, C, 1, 1)
    return y

输入特征 $\mathbf{X}$ 经过 LayerNorm 标准化后，MFF 使用了三个分支来对其进行信息抽取与综合，包括 Channel Attention，Depthwise Convolution，以及 KBA 模块。Channel Attention 用于融合特征通道间的信息，主要通过一个 Global Average Pooling 与 1x1 Convolution 来实现，也就是类似于 Squeeze-and-Excitation Block (Hu et al.) 的结构。Depthwise Convolution 用于学习特征中的 Spatially-Invariant 信息。KBA 模块即实现特征像素自适应的注意力机制。三者通过 Point-wise 相乘来达到类似于 GLU 与 SimpleGate 门控非线性激活函数。最后，一个 1x1 Convolution 再次进行通道间的信息融合，并通过一个可学习权重加权的 Skip-connection 来降低 MFF 模块的学习难度与提高稳定性。类似于 Transformer，MFF 最后在具体实现中也在最后增加了一个 Feed Forward Network (FFN)，其主要通过两个相连的 1x1 Convolution 对通道特征进行强化，最后通过另一个可学习权重加权的 Skip-connection 获得 MFF 的输出。MFF 的代码如下：

''' Channel Attention
1. global average pooling to NxCx1x1
2. channel attention by 1x1 convolution
'''
self.sca = nn.Sequential(
    nn.AdaptiveAvgPool2d(1), # equivalent to global average pooling
    nn.Conv2d(in_channels=c, out_channels=c, kernel_size=1, padding=0, stride=1, groups=1, bias=True),
)

''' DWConv
1. 1x1 convolution
2. 3x3 grouping convolution, groups=c, i.e. depthwise
'''
self.conv11 = nn.Sequential(
    nn.Conv2d(in_channels=c, out_channels=c, kernel_size=1, padding=0, stride=1, groups=1, bias=True),
    nn.Conv2d(in_channels=c, out_channels=c, kernel_size=3, padding=1, stride=1, groups=c, bias=True),
)

''' post 1x1 convolution
'''
self.conv3 = nn.Conv2d(in_channels=dw_ch // 2, out_channels=c, kernel_size=1, padding=0, stride=1, groups=1, bias=True)

''' FFN
'''
self.conv4 = nn.Conv2d(in_channels=c, out_channels=ffn_ch, kernel_size=1, padding=0, stride=1, groups=1, bias=True)
self.conv5 = nn.Conv2d(in_channels=ffn_ch // 2, out_channels=c, kernel_size=1, padding=0, stride=1, groups=1, bias=True)

''' learnable weights
'''
self.attgamma = nn.Parameter(torch.zeros((1, self.nset, 1, 1)) + 1e-2, requires_grad=True)
self.ga1 = nn.Parameter(torch.zeros((1, c, 1, 1)) + 1e-2, requires_grad=True)
self.beta = nn.Parameter(torch.zeros((1, c, 1, 1)) + 1e-2, requires_grad=True)
self.gamma = nn.Parameter(torch.zeros((1, c, 1, 1)) + 1e-2, requires_grad=True)

self.sg = SimpleGate()                   
self.norm1 = LayerNorm2d(c)
self.norm2 = LayerNorm2d(c)

def forward(self, inp):
    x = inp
    # LayrNorm
    x = self.norm1(x)
	# channel attention
    sca = self.sca(x)
    # DWConv
    x1 = self.conv11(x)
    # KBA module
    att = self.conv2(x) * self.attgamma + self.conv211(x)
    uf = self.conv21(self.conv1(x))
    # KBA with weighted skip-connection
    x = self.KBA(uf, att, self.k, self.g, self.b, self.w) * self.ga1 + uf
    # branch compose
    x = x * x1 * sca
    # post 1x1 conv
    x = self.conv3(x)
    # MFF skip-connection
    y = inp + x * self.beta
    # FFN
    x = self.norm2(y)
    x = self.conv4(x)
    x = self.sg(x)
    x = self.conv5(x)
	# FFN skip-connection
    return y + x * self.gamma

4 参考文献

• Zhang Y, Li D, Shi X, et al. KBNet: Kernel Basis Network for Image Restoration[J]. arXiv preprint arXiv:2303.02881, 2023.
• Wang Z, Cun X, Bao J, et al. A General U-Shaped Transformer for Image Restoration. arXiv 2021[J]. arXiv preprint arXiv:2106.03106.
• Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[J]. Advances in neural information processing systems, 2017, 30.
• Hu J, Shen L, Sun G. Squeeze-and-excitation networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 7132-7141.