如何判断两架飞机在汇聚飞行?(如何计算两架飞机的航向夹角?)内含程序源码
ok,在开始一切之前,让我先猜一猜,你是不是想百度“二维平面下如何计算两个移动物体的航向夹角?”如果是,那就请继续往下看。
首先,我们要明确一个概念:航向角≠航向夹角!!!!!!我说的是航向夹角,我可跟那** 百度不一样,*百度一搜航向夹角,全**弹出来的是航向角。
“Angle Off”(夹角)是用来描述一架飞机与另一架的优势或劣势关系的术语。 是你和敌机航向之间的夹角,用度为单位表示。如果你敌机之间的航向一致,那么你的夹角就是 0°;而 90°夹角就说明你垂直于敌机。夹角也被称之为 HCA(航向夹角 Heading Crossing Angle)。
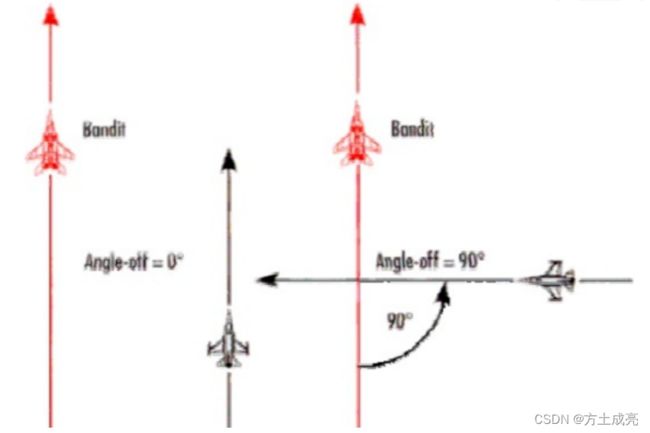
什么是汇聚飞行?
什么是分散飞行?
上图即为分散飞行示意图,红色的箭头是飞机飞行的速度方向。
OK!!我们的标题是——如何判断两架飞机在汇聚飞行?答案是:请告诉我你两架飞机的飞行坐标(x,y)以及你两架飞机的飞行速度(V_x,V_y)!!
路人:飞机,飞机,都飞起来了,你这飞机怎么没有高度z和z轴的速度的?
我:我把3维的空间全当做二维的平面处理了,这篇博客全都是从二维平面的角度出发的。因为3维变二维可以大大简化我的工作量,3维会导致我猪脑过载,猪脑的CPU容易冒烟,望李姐。
路人:只给两架飞机的速度信息(V_x,V_y),还不能判断飞机是在汇聚还是在分散飞行吗?
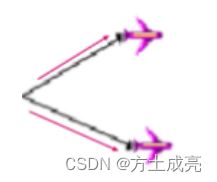
上图中,飞机的航向夹角都是45°,但是由于飞行起点的不同,左边的两架飞机是在汇聚飞行,将交于一点,而右边的两架飞机则是在分散飞行,它们只会越飞越远。
使用我下面给出的这一段python程序,就能判断出两架飞机是在汇聚还是在分散飞行,并且能得到两架飞机的航向夹角。函数的输入参数是:飞机一的坐标(x,y),速度(vx,vy),飞机二的坐标(X,Y),速度(Vx,Vy),航向夹角可以根据高中数学课本中的两矢量夹角公式求得:

而关于飞机汇聚飞行和分散飞行的判断,我的处理方法是:计算当前时刻k下两架飞机的二范数,再计算下一时刻k+1下两架飞机的二范数,如果当前时刻的范数大于下一时刻的范数,就意味着两架飞机越飞越近,就是汇聚飞行,反之亦然。
至此,代码如下,拿走不谢,复制即用,不行砍我!
import math
x,y,vx,vy=0,0,1,0#飞机一参数
X,Y,Vx,Vy=0,-1,1,1#飞机二参数
def ddd(x,y,vx,vy,X,Y,Vx,Vy):
angle=math.acos((vx*Vx+vy*Vy)/(math.hypot(vx,vy)*math.hypot(Vx,Vy)))*180/math.pi
dis1=math.hypot((x-X),(y-Y))
dis2=math.hypot((x+vx)-(X+Vx),(y+vy)-(Y+Vy))
if dis1>dis2:
print('汇聚')
elif dis1<dis2:
print('分散')
else:
print('静止没变')
print('航向夹角:',angle)
ddd(x,y,vx,vy,X,Y,Vx,Vy)
参考文献:
知乎的一篇文章
一篇硕士学位论文