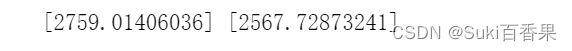02-梯度下降法实践

（一）梯度下降法最简步骤

（二）BGD线性回归代码实现

1.生成回归数据

 2.拆分训练集与测试集

3.利用梯度下降法拟合直线y=wx+b

（一）梯度下降法最简步骤

求使得f(w)值最小的参数w

初始化 

for t =1,2,...:

      

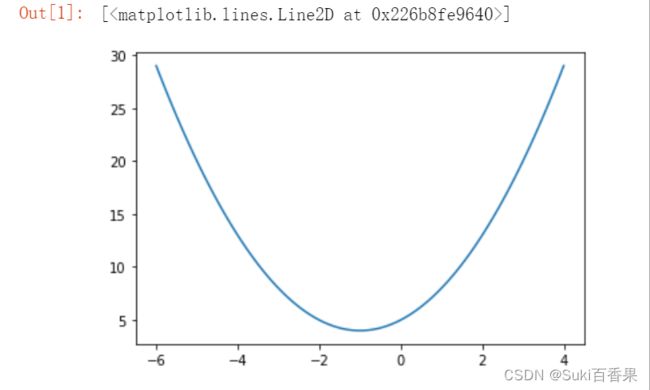
使用numpy和matplotlib绘制曲线y=x^2+2x+5

首先生成从-6到4的100个x值

再利用公式赋值给y

最后使用plt.plot(）绘制曲线

#绘制曲线 y=x^2+2x+5
import numpy as np
import matplotlib.pyplot as plt
#生成从-6到4的100个数
x=np.linspace(-6,4,100)
y=x**2+2*x+5
plt.plot(x,y)

梯度下降法寻找最小值、最小值点和迭代次数（使用while True循环构建）

#参数初始化
x_iter = 3 #x的初值
yita =0.06#步长
count=0#迭代次数
while True:
    count+=1
    y_last = x_iter**2+x_iter*2+5
    x_iter=x_iter-yita*(2*x_iter+2)
    y_next=x_iter**2+x_iter*2+5
    if abs(y_next-y_last)< (1e-100):  #1e-100为较小的数
        break
print("最小值点x=",x_iter,'最小值y=',y_next,'迭代次数为',count)

绘制曲线并标注每个点的位置、迭代次数

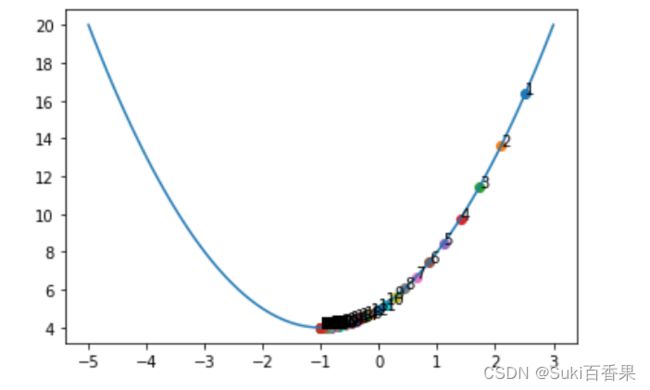
x_iter = 3 #x的初值
yita =0.06#步长
count=0#迭代次数
while True:
    count+=1
    y_last = x_iter**2+x_iter*2+5
    x_iter=x_iter-yita*(2*x_iter+2)
    y_next=x_iter**2+x_iter*2+5
    plt.scatter(x_iter,x_iter**2+x_iter*2+5)#标注每个点的位置
    plt.annotate(count,(x_iter,x_iter**2+x_iter*2+5))#标注迭代次数
    if abs(y_next-y_last)< (1e-100):
        break
print("最小值点x=",x_iter,'最小值y=',y_next,'迭代次数为',count)
x=np.linspace(-5,3,100)
y=x**2+2*x+5
plt.plot(x,y)

 修改步长（只是更换了初始值）

#修改步长为0.8
x_iter = 3 #x的初值
yita =0.8#步长
count=0#迭代次数
while True:
    count+=1
    y_last = x_iter**2+x_iter*2+5
    plt.scatter(x_iter,x_iter**2+x_iter*2+5)
    plt.annotate(count,(x_iter,x_iter**2+x_iter*2+5))
    x_iter=x_iter-yita*(2*x_iter+2)
    y_next=x_iter**2+x_iter*2+5
    if abs(y_next-y_last)< (1e-100):
        break
print("最小值点x=",x_iter,'最小值y=',y_next,'迭代次数为',count)
x=np.linspace(-5,3,100)
y=x**2+2*x+5
plt.plot(x,y)

可以发现，步长较长，在左右振荡几个来回后，最后还是能找到最小值点。 

（二）BGD线性回归代码实现

BGD：批量梯度下降法

1.生成回归数据

from sklearn.datasets import make_regression
X,y=make_regression(n_samples=100,n_features=1,noise=50,random_state=8)
plt.scatter(X,y)

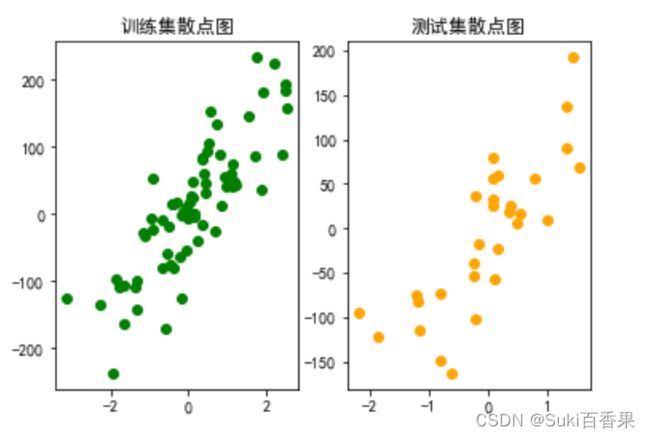
 2.拆分训练集与测试集

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=30,random_state=8)
#绘制训练集散点图
plt.subplot(1,2,1)
plt.scatter(X_train,y_train,c='g')
plt.title("训练集散点图")
#绘制测试集散点图
plt.subplot(1,2,2)
plt.scatter(X_test,y_test,c='orange')
plt.title("测试集散点图")
#中文
plt.rcParams['font.sans-serif']=['SimHei','Times New Roman']
plt.rcParams['axes.unicode_minus']=False

3.利用梯度下降法拟合直线y=wx+b

3.1参数初始化

w=1                 #直线斜率
b=-100              #直线截距
lr=0.001            #步长/学习率learning rate

3.2针对参数w和b，先分别计算求和号的值

sum_w=0
sum_b=0
for i in range(len(X_train)):
    y_hat = w*X_train[i]+b
    sum_w +=(y_train[i]-y_hat)*X_train[i]
    sum_b +=y_train[i]-y_hat

3.3更新w与b的值

w +=lr *sum_w
b +=lr*sum_b

3.4  将3.2与3.3重复迭代epochs次

w=1                 
b=-100              
lr=0.001            
epochs = 1000
for j in range(epochs):
    sum_w=0
    sum_b=0
    for i in range(len(X_train)):
        y_hat = w * X_train[i] + b
        sum_w += (y_train[i] - y_hat) * X_train[i]
        sum_b += y_train[i] - y_hat
    #更新参数w与b
    w += lr * sum_w
    b += lr * sum_b

3.5 将迭代结果数据可视化

xx = np.linspace(-4,4,100)
yy = w * xx + b
plt.scatter(X_train,y_train,c='g')
plt.plot(xx,yy)
plt.title("线性回归拟合图")
plt.legend(("拟合直线",'训练集散点'))

 

3.6 计算在训练集和测试集上的均方误差

total_loss_train=0
for i in range(len(X_train)):
    y_hat = y_hat =w * X_train[i] + b
    total_loss_train += (y_hat - y_train[i]) ** 2

total_loss_test = 0
for i in range(len(X_test)):
    y_hat = y_hat =w * X_test[i] + b
    total_loss_test += (y_hat - y_test[i]) ** 2

print(total_loss_train/len(X_train),total_loss_test/len(X_test))

 

 ps:均方误差是用来衡量观测值（真值）与预测值之间的偏差。

所以，可以知道训练集和测试集上的均方误差较大，模型拟合的并不是很好。