【JavaScript算法实践】最短路径算法

---

前言

最短路问题是图问题中的经典问题，这类问题在生活中非常常见，我们（特别是生活在大城市的人）出门在外，无论是驾车还是乘坐公共交通工具，甚至步行，都会求助于高德地图、百度地图等定位和导航程序。我们可能会有其他的考虑：例如如何乘车、换乘？如何避开拥堵路段？但根本的问题仍然是：哪条路径最短？
在图问题中，这一问题对应的算法被称为最短路径算法。本文介绍其中两种非常著名算法的JavaScript实现：
Dijkstra算法和Floyd-Warshall算法
关于Dijkstra算法 和 Floyd-Warshall算法可以参考以下博文
Dijkstra算法
Floyd-Warshall算法

---

一、Dijkstra算法

Dijkstra算法是一种计算从单个源到所有其他源的最短路径的贪心算法，这意味着我们可以用它来计算从图的一个顶点到其余各顶点的最短路径

考虑下图：

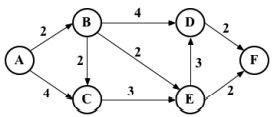
我们来看看如何找到顶点A和其余顶点之间的最短路径。但首先，我们需要声明表示上图的邻接矩阵，如下所示：

var graph = [[0,2,4,0,0,0],
            [0,0,2,4,2,0],
            [0,0,0,0,3,0],
            [0,0,0,0,0,2],
            [0,0,0,3,0,2],
            [0,0,0,0,0,0]]

算法实现

下面给出Dijkstra算法的实现：

this.dijkstra = function(src){ //输入参数src为源节点索引，例如A点的索引是0，B点是1
	var dist = [], //最短路径距离
	visited = [], //已访问
	length = this.graph.length //最长路径距离
	
	for(var i = 0; i < length; i++){
		dist[i] = Infinity   //先初始化为无穷大
		visited[i] = false // 初始化标记均未访问
	}
	dist[src] = 0 //起点最短距离设置为0
	
	for(var i = 0; i < length-1; i++){
		var u = minDistance(dist, visited) //寻找最短路
		visited[u] = true; //标记为已访问
		for(var v = 0; v < length; v++){
			if(!visited[v] && this.graph[u][v] != 0 && dist[u] != Infinity  &&
			dist[u] + this.graph[u][v] < dist[v]) {
				dist[v] = dist[u] + this.graph[u][v] //若找到更短路，更新
			}
		}
	}
	return dist;//处理完所有节点，返回源点到其他顶点的最短路径距离向量
}

计算顶点间最短路径minDistance，需要搜索dist向量中的最小值，返回它在数组中的索引：

var minDistance = function(dist, visited){
	var min = Infinity, minIndex = -1
	for(var v = 0; v < dist.length; v++){
		if(visited[v] == false && dist[v] <= min){
			min = dist[v]
			minIndex = v
		}
	}
	return minIndex
}

若选A为源节点，对本节开始的图执行以上算法

this.dijkstra(0)

会得到如下输出：

说明：本算法实现只求得了源节点到其他节点的最短路长度，没有给出具体路径。

二、Floyd-Warshall 算法

Floyd-Warshall算法是一种计算图中所有最短路径的动态规划算法。通过该算法，我们可以找出从所有源到所有顶点的最短路径。

算法实现

this.floydWarshall = function(){
	var dist = [],
	length = this.graph.length,
	i,j,k
	for(i = 0; i < length; i++){
		dist[i] = []
		for(j = 0; j < length; j++){
			//录入一步直达路径
			if(this.graph[i][j] == 0 && i != j) {
				dist[i][j] = Infinity
			}else{
				dist[i][j] = this.graph[i][j]
			} 
			console.log(dist[i][j])
		}
	}
	for(k = 0; k < length; k++){ //k是中间节点
		for(i = 0; i < length; i++){ //i是起点
			for(j = 0; j < length; j++){ //j是终点
				if((dist[i][k] + dist[k][j]) < dist[i][j]) //如果i经过k，到达j的路径比已有的最短路径更短
					dist[i][j] = dist[i][k] + dist[k][j] //则更新
			}
		}
	}
	return dist
}

this.floydWarshall()

会得到如下输出：

其中，Infinity代表顶点 i 到 j 的最短路径不存在。