【python】数据挖掘分析清洗——特征选择（特征筛选）方法汇总

本文链接：https://blog.csdn.net/weixin_47058355/article/details/130400400?spm=1001.2014.3001.5501

前言

特征构造得到足够的广度后，将这些特征进行筛选
特征选择主要有两个功能：
减少特征数量、降维，使模型泛化能力更强，减少过拟合
增强对特征和特征值之间的理解

通常来说，从两个方面考虑来选择特征：

特征是否发散：如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。

特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择

数据展示：

一、过滤法

过滤法根据我的理解，就是通过统计学的方法对数据进行判断处理

1.1 基于方差

通过方差来判断数据是否发散，最后根据发散结果，判断是否删除该数据

# 对方差的大小排序
data.std().sort_values()    # select_data是final_data去掉了独热的那些特征
#去掉变化小的特征 比如一个特征如果全是1或者0 那么这数据是没有意义的

根据排序好的数据，选择结果为0的数据删除或者小于某个阈值进行列删除以此来进行特征选择

1.2 相关系数

相关系数是用于衡量两个变量之间线性关系紧密程度的统计量。其取值范围在-1到1之间，其中1表示完全正相关，-1表示完全负相关，0表示没有线性关系。通常用符号r表示相关系数。
常用的有pearson系数还有spearman系数

import matplotlib.pyplot as plt
corr = data.corr('pearson')    # .corr('spearman')
#corr得到特征与特征之间的相关性 然后corr['target']就是目标特征与所有特征之间的相关性
#利用corr方法得出特征的pearson或spearman系数值
plt.rcParams['font.family']=['Microsoft YaHei']
plt.figure(figsize=(5,5)) #将结果画图表示
corr['是否在当年造假'].sort_values(ascending=False)[1:].plot(kind='bar')#一般是使用标签作为相关性计算的列
plt.tight_layout()

或者用热力图进行可视化

import seaborn as sns
# 用热力图看一下互相之间的关系
f, ax = plt.subplots(figsize=(10, 10))#设置大小
sns.heatmap(corr, annot=True)# annot表示是否在方块上出现数字

这里小结一下常用相关系数
在统计学中，常用的相关系数有以下几种：

Pearson 相关系数：它是最常用的相关系数，用于衡量两个连续变量之间的线性关系。当数据近似正态分布时，它通常是最好的选择。

Spearman
相关系数：它是一种非参数方法，用于衡量两个变量之间的单调关系，不要求变量呈线性关系。它的计算方法是将原始数据转换为等级（排序）数据，然后计算等级数据之间的
Pearson 相关系数。

Kendall 相关系数：它也是一种非参数方法，用于衡量两个变量之间的单调关系，在一些情况下比 Spearman
相关系数更适用。它的计算方法是计算两个变量之间的等级协同对数。

切比雪夫相关系数：它用于衡量两个变量之间的距离或差异，它是两个变量之间最大差异的绝对值。

Eta 相关系数：它用于衡量两个分类变量之间的关系，可以看作是 Pearson 相关系数的变体。

互信息：它用于衡量两个变量之间的非线性关系，特别是在存在多元关系和噪声干扰的情况下。

在实际应用中，根据具体数据类型和研究目的可以选择不同的相关系数进行计算。

不同的相关系数有不同的计算方法和应用场景，它们之间的差别和优点如下：

Pearson:相关系数：用于衡量两个连续变量之间的线性关系。具有计算简单、解释方便、可比性强等优点，但缺点是对异常值敏感，对非线性关系不敏感。
Spearman: 相关系数：用于衡量两个变量之间的单调关系。它具有不受异常值影响、不要求数据呈正态分布等优点，适用于非线性单调关系的情况，但是可能会忽略掉数据间的差异信息。

Kendall 相关系数：也用于衡量两个变量之间的单调关系。与 Spearman
相关系数相比，它更加稳健，能够有效处理小样本问题，但是计算复杂度较高。

切比雪夫相关系数：用于衡量两个变量之间的距离或差异。它具有不受数据分布和缩放影响的优点，但是对于极端异常值的情况，可能不够稳健。

Eta 相关系数：用于衡量两个分类变量之间的关系。由于是基于卡方检验的效果量，因此具有显著性水平的信息，但是只能处理两个变量之间的关系。

互信息：用于衡量两个变量之间的非线性关系。它比 Pearson
相关系数更加灵活，能够处理多元关系和噪声干扰的情况，但是计算复杂度较高，需要大量的样本数据支持。

综上所述，不同的相关系数适用于不同的数据类型和研究目的，选择合适的方法能够得到更准确的结果。

二、包裹式

包裹式从初始特征集合中不断的选择特征子集，训练学习器，根据学习器的性能来对子集进行评价，直到选择出最佳的子集。包裹式特征选择直接针对给定学习器进行优化。
（简单来说就是把特征拆成一个个，然后学习，通过模型评分判断特征的相关性)

2.1 随机森林

使用随机森林作为模型对数据进行筛选

#正常的处理 将单个特征挨个进行评分
from sklearn.model_selection import cross_val_score, ShuffleSplit
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import KFold
import numpy as np

X = data.iloc[:,:-1]
Y = data['是否在当年造假']
names = X.columns

rf = RandomForestRegressor(n_estimators=20, max_depth=4)
kfold = KFold(n_splits=5, shuffle=True, random_state=7)
scores = []
for column in X.columns:
    print(column)
    tempx = X[column].values.reshape(-1, 1)
    score = cross_val_score(rf, tempx, Y, scoring="r2",error_score='raise',
                              cv=kfold)
    scores.append((round(np.mean(score), 3), column))
print(sorted(scores, reverse=True))

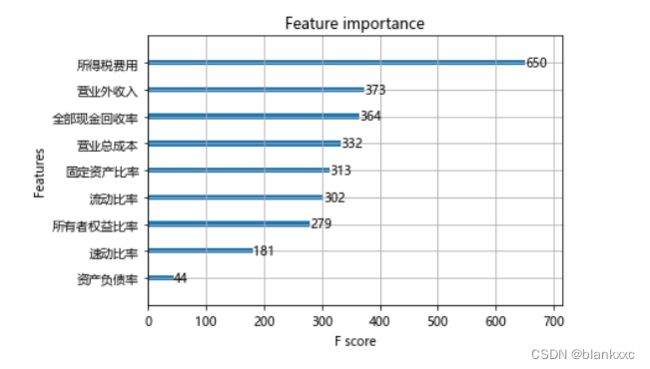
2.2 XGBoost重要性分析

利用XGBoost的梯度提升树，判断特征在每个决策树的重要程序之后，将其按一定权重进行相加处理。

# 下面再用xgboost跑一下 xgboost有专门的一个特征评测体系
from xgboost import XGBRegressor
from xgboost import plot_importance

xgb = XGBRegressor()
xgb.fit(X, Y)

plt.figure(figsize=(20, 10))
plot_importance(xgb)
plt.show()

2.3 SFS序列前向选择算法（Sequential Forward Selection）

基于随机森林回归器（RandomForestRegressor）的序列前向选择算法（Sequential Forward Selection）

#利用SFS进行特征的排序
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
# sfs = SFS(LinearRegression(), k_features=20, forward=True, floating=False, scoring='r2', cv=0)
sfs = SFS(RandomForestRegressor(n_estimators=10, max_depth=4), k_features=5, forward=True, floating=False, scoring='r2', cv=0)
# RandomForestRegressor(n_estimators=10, max_depth=4)：使用10个决策树，每棵决策树最大深度为4的随机森林回归器。
# k_features=5：最终选择出来的特征数量。
# forward=True：使用序列前向选择算法进行特征选择。
# floating=False：不使用悬浮搜索算法。
# scoring='r2'：评估指标为R方（coefficient of determination）。
# cv=0：交叉验证的折数。由于该参数值为0，因此没有使用交叉验证，而是直接使用默认的训练集和测试集进行模型训练和评估。
X = data.iloc[:,:-1]
Y = data['是否在当年造假']

sfs.fit(X, Y)
sfs.k_feature_names_   

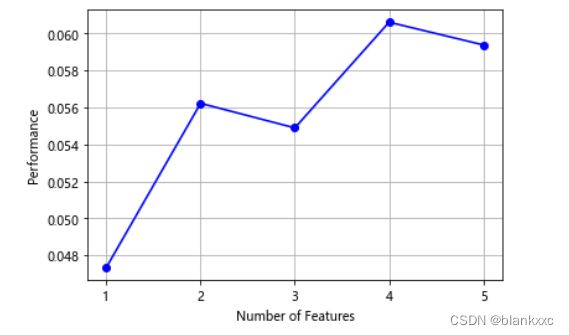
#画出sfs的特征的前几项的边际效应 
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
fig1 = plot_sfs(sfs.get_metric_dict(), kind='std_dev')
plt.grid()
plt.show()

三、嵌入式

嵌入式特征筛选是一种机器学习中常用的特征选择方法，它在模型训练过程中直接考虑了特征的重要性，通过将特征的权重嵌入到模型的训练中进行特征选择。

具体来说，在嵌入式特征筛选中，算法会自动选择与目标变量最相关的特征，同时也会惩罚那些对模型贡献较小的特征。这样可以有效地防止过拟合问题，并且在一定程度上提高了模型的解释能力。

在实际应用中，嵌入式特征筛选常常和各种机器学习算法一起使用，例如线性回归、逻辑回归、支持向量机等。

3.1 SVC

这里是以SVC为例

from sklearn.svm import LinearSVC
from sklearn.feature_selection import SelectFromModel

X = data.iloc[:,:-1]
Y = data['是否在当年造假']

# 注意：dual 设置为 False，否则会报错
model_lsvc = LinearSVC(penalty='l1', C=0.2, dual=False)#设置模型
model_lsvc.fit(X,Y)
#penalty：惩罚项，指定正则化策略。'l1'表示使用L1正则化，'l2'表示使用L2正则化。
#C：正则化系数，控制模型的复杂度和拟合程度，值越小表示正则化强度越高，模型越简单。
#dual：对偶或原始问题的求解方法，当样本数量大于特征数量时，通常dual=False可以更快地求解。
#下面是将特征筛选的结果用特征名表示
df_0=pd.DataFrame(X.columns)
df=pd.DataFrame(list(model_lsvc.coef_))
df2 = pd.DataFrame(df.values.T, index=df.columns, columns=df.index)#转置
df3=pd.concat([df_0,df2],axis=1)
df3.columns=['特征','权重']
list(df3[df3['权重']!=0]['特征'])

总结

特征选择指的是从原始数据中选择最具有代表性和重要性的特征，保留这些特征并去除无用或冗余的特征。它的主要目的是：

提高模型的准确性和精度：通过筛选和保留最重要的特征，可以消除噪声或不相关特征的干扰，提高模型的预测准确性和精度。

降低过拟合风险：在特征数量较多时，模型容易出现过拟合的问题，即在训练集上表现良好，但在测试集上表现差。通过特征选择可以降低特征数量，减少模型的复杂度，从而降低过拟合风险。

缩短训练时间和节省计算资源：特征选择可以减少需要处理的数据量，从而缩短训练时间和节省计算资源。

提高可解释性和可视化效果：特征选择可以使得模型的特征更加直观和可解释，便于后续的可视化分析和解释。

总之，特征选择对于构建高质量、高效率和易解释的机器学习模型非常重要。
除了特征选择，还有另外一种特征筛选的方法就是降维，这个我放在另外一篇博客讲。
如果这篇博客对你有帮助的话，可以给我点赞收藏评论！