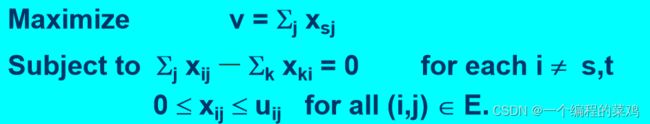python实现最大流算法(Push-Relabel算法)-图算法
一.最大流问题
二.解决最大流的相关算法Push-Relabel算法
二.伪代码
push-relabel伪代码:
Initialize();
WHILE 存在盈余点 DO
选择最大高度盈余点v;
IF ∃e(v,w)满足h(v)=h(w)+1
THEN Push( v, e);
ELSE h(v)++; //Relabel
ENDWHILE
push的伪代码:
IF α_f(v)≥r_e THEN
Δ=r_e; //饱和推送
ELSE
Δ=α_f(v); //非饱和推送
在边e上推送Δ单位的流;
更新剩余容量r_e Initialize()伪代码(高度不变式):
f=0;
“反向BFS”设置高度值;
h(s)=n;
FOR v∈δ^+(s) DO
在e(s,v)上饱和推送;
ENDFOR
三.项目代码
from collections import defaultdict
edges=defaultdict(list)#记录每条边的容量和边的信息
nodes=[]#记录图中的点
profit={}#记录每个点的盈余,前提是顶点是已经编号好的
opposite_edges=defaultdict(list)
def read_file(filepath,nodes,edges,opposite_edges):
"""读取文件数据"""
f=open(filepath,"r");
graph_node_num=int(f.readline().strip())
graph_edge_num=int(f.readline().strip())
for _ in range(graph_edge_num):
node_a,node_b,edge_c=f.readline().split()
if node_a not in nodes:
nodes.append(node_a)
if node_b not in nodes:
nodes.append(node_b)
edges[node_a].append([node_a,node_b,int(edge_c)])
opposite_edges[node_b].append((node_b,node_a))
start_node,end_node=f.readline().split()
return start_node,end_node,graph_node_num
def BFS(opposite_edges,end_node,Hight):
"""BFS反向设置层号+层号就是高度"""
queue=[]#设置一个队列
visited=[]
visited.append(end_node)
for i in opposite_edges[end_node]:
node_a,node_b=i
queue.append(node_b)
visited.append(node_b)
Hight[int(node_b)]=Hight[int(node_a)]+1
while len(queue)!=0: #队列不为空就一直进行循环
node=queue.pop(0)
for i in opposite_edges[node]:
node_c,node_d=i
if node_d not in visited: #邻接点没有被探索,就高度加1,并把这个邻接点加入队列
Hight[int(node_d)]=Hight[int(node_c)]+1
queue.append(node_d)
visited.append(node_d)
pass
pass
def push(node_a, edge, node_b, profit, edges):
"""push操作"""
if profit[node_a] >= edge: # 饱和推送
flow_edge = edge
else: # 非饱和推送
flow_edge = profit[node_a]
profit[node_a] = profit[node_a] - flow_edge # 更新node_a点上的盈余
profit[node_b]=profit[node_b]+flow_edge #更新node_b点上的盈余
flag=1 #设置一个标志位
k=0
for line in edges[node_b]: #如果以前存在这条反向边,更新
if line[1]==node_a :
edges[node_b][k][2]= edges[node_b][k][2]+flow_edge
flag=0
break
k=k+1
if flag==1: #之前不存的话,就增加
edges[node_b].append([node_b,node_a,flow_edge])
j = 0
#更新原来边上的容量
for i in edges[node_a]:
if i[1] == node_b:
edges[node_a][j][2]=edge-flow_edge
j=j+1
def initialize(opposite_edges,edges,nodes,start_node,end_node,Hight,graph_node_num,profit):
"""初始化操作"""
Hight[int(end_node)]=0
BFS(opposite_edges,end_node,Hight)#BFS反向设置层号
Hight[int(start_node)]=graph_node_num #保持高度不变式
for i in nodes:
profit[i]=0 #初始化,所有点的盈余为0
k=0
for line in edges[start_node]: #设置起始点的盈余
profit[start_node]=profit[start_node]+line[2]
for line in edges[start_node]:
node_a,node_b,edge_c=line
push(node_a,edge_c,node_b,profit, edges) #在起点的所有邻接边上进行推送
def select_high(Hight,profit,nodes,start_node,end_node):
"""选择最大高度的盈余点"""
max=0
for i in nodes:
if i !=start_node and i !=end_node:
if profit[i]!=0: #先确保有盈余
if Hight[int(i)]>=max: #选择高度最大
max=Hight[int(i)]
node=i
return node
def Push_Relabel(edges,nodes,start_node,end_node,opposite_edges,Hight, graph_node_num,profit):
"""push和Relabel操作"""
initialize(opposite_edges, edges,nodes,start_node, end_node, Hight, graph_node_num,profit)
ans=1
while ans!=0:
#选择最大高度的盈余点
node_v=select_high(Hight,profit,nodes,start_node,end_node)
flag=1#设置一个标志位
for line in edges[node_v]: #寻找node_v的邻接边,发现有满足的“下山”方向的边就进行push操作
node_v,node_w,edge_c=line
if Hight[int(node_v)]==(Hight[int(node_w)]+1) and edge_c!=0: #满足高度不变式,并且边存在的话
push(node_v,edge_c,node_w,profit,edges)
flag=0
if flag==1: #不存在这样的边就进行relabel操作
Hight[int(node_v)]=Hight[int(node_v)]+1
ans = 0
for i in profit.values():
ans = ans + i
ans = ans - profit[end_node] - profit[start_node] #计算V-{s,t}中所有点中的盈余 盈余为0时,证明已经找到了最大流
start_node,end_node,graph_node_num=read_file("project9-test3",nodes,edges,opposite_edges)
Hight=[0]
for i in nodes:
Hight.append(0)
Push_Relabel(edges,nodes,start_node,end_node,opposite_edges,Hight, graph_node_num,profit)
print("最大流为:",profit[end_node])