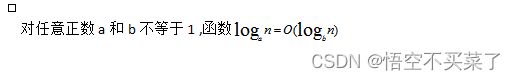算法的时间复杂度分析

目录

什么是算法

计算机算法的五个基本特征

算法时间评估简单描述 

时间复杂度的大O来表示法

大O表示法的一些常见性质

常见的函数时间复杂度关系

时间复杂度分析习题讲解

---

什么是算法

解题方案的准确而完整的描述，解决某一问题的计算方法

计算机算法的五个基本特征

算法时间评估简单描述 

评估一个算法的效率，不能使用什么实时的计量单位，比如秒啊，微妙啊啥的，最好用逻辑单位，他能表示数据规模N与时间t的这样一种关系，然后分析这种关系的增长曲线

影响一个算法的因素也有很多，比如机器运行的快慢，比如数据的规模，比如语言的高级程度等等，都决定了这个算法需要耗费的时长。

一般一个算法我们都会用数据规模N与时间t关联的函数表示，然后取函数项里面增长最快的一项作为算法时间复杂度。

我们考虑算法的时候，主要考虑问题规模特别大的时候，小数据规模，你的算法是什么时间复杂度，影响都没有多大，这也是我们经常分析问题的一种思维，考虑问题，我们一般要考虑最坏的情况。

函数增长最快一项与问题规模特别大这个其实相互独立，每一个函数问题规模都可以增大，也都有增长速率，但是我们主要去研究函数的增长速率。

比如一个函数f(x)=n^2+100*n+1+2^n

上面有一种很明显的时间复杂度关系：2^n>n^2>100*n>1

也就是说当数据足够大的时候，我们主要去关注函数增速最快的一项，在分析n的取值的时候，也要保证最快的一项始终是增长最快的一项。

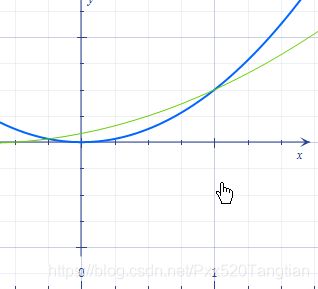
下面用一个图像来看与幂函数与指数函的增长情况：

绿色代表2^n(指数在不停改变) 蓝色代表n^2（幂函数）,在最开始数据规模比较小的是时候，很明显n^2>2^n,但是我们去看一下数据规模超过了一定的值之后，函数情况是怎么发生改变的。

很明显2^n远远大于n^2的数值增长。

时间复杂度的大O来表示法

定义：存在一个正数c与N,对于所有的n>=N,也即是一个问题规模的临界点，f(n)<=cg(n)，此时f(n)=O(g(n)),这个g(n)函数就代表了时间复杂度（我们可以用常见的算法时间复杂度去分析）

现在我们来重点讲解一下上面这句话：

假设一个函数的运行次数的函数是f(n)=2*n^2+3*n+1,那么这个时候，我们把g(n)考虑成它增长最快的一项f(n)=O(n^2);

此时我们来分析一下N与c的值：

也就是不同的c取值对应的g(n)函数与f(n)的交点（交点也不一样），然后取出来的N是不一样的。

假设N取1,2,3,4..我们来分析一下图像：

上面就是y=6*x^2(蓝色)与y=2*x^2+3*x+1(绿色)的对比图像，很明显可以看见，他们交互的n=1,当n>1，g(n)完全大于f(n),所以，我们就可以列出c与N取值对照表

N   1      2

c   >=6    >=3.75  .......

上面好像就是通过大N来决定C的取值，他们必定有一个相同的值进行交会，这个定理好像就是一个验证。

也即是n>=N，然后g(n)完全大于f(n)的条件是c必须大于等于某一个数，然后两个函数恰好交互在某一个数上面。

再来分析一下原函数2*n^2+3*n+1<=cn^2   ===>   2+3/n+1/n^2<=c  =====>

根据n来推算出c，根据原函数取值就可以算出来。，因为他们必定有一个交点。

那么我们如何选择合适的c与N呢？，我们最好看哪一个N可以让f增长最快的某一项始终保持最大，上面原函数最大项是2*n^2与3^n,如果N取1，那么不等式2*n^2>3*n就不满足，那么如果N=2，2*n^2>3*n .因为毕竟c是通过N进行推算出来的。

其实上面就是想说，对于一个给定函数f,有无穷多的g与之对应，原函数不仅仅是O(n^2)的g函数，还可以是n^3,n^4,也就是只要满足fn<=cg(n),这样的条件都可以，为了避免这种情况，我们一般选择较小的函数g来表示算法时间复杂度，比如2次幂就差不多了。

大O表示法的一些常见性质

性质1：传递性

f(n)=O(g(n))  g(n)=O(h(n)))   ===>  f(n)=O(h(n))，而g(n)的时间复杂度就等于它本身的时间复杂度

原函数的时间复杂度等于g(n)的时间复杂度

证明也很简单：

f(n)=O(g(n))  g(n)=O(h(n))  =>  f(n) = O(h(n))

我们知道f(n) <= c1g(n)，

那么对于g(n)与h(n)来说，g(n) <=c2(h(n)),

=>f(n) <= c1*c2h(h),此时把c1与c2看成c=>f(n) <= c(h(n))

上面这种关系我们用三个函数模拟一下

f(n)=2n^2+3n+1

g(n)=n^2

h(n)=n^2

现在我们假设，上面论证了c>=6 N=1,也就是说c1我就取6  ==> f(n)<=c1g(n),此时g(n)是fn的一个时间复杂度。c1=6 N1=1

好，这里我们又假设g(n)<=c2h(n)  那么c1=6,我们只要c2>6就可以大于g(n)的函数了并且大于N=1时的f(n)函数，我们比如c2取7, h(n)=n^2,那么N2只能取0，（这里的意思就会使6*n^2 == 7*n^2,这里n只能取0）只要大于N>0，c2h(n)就始终大于g(n),要也就是g(n)<=7h(n),此时h(n)就是它的算法时间复杂度。

ok,那么我们现在知道了几个条件

c1=6 N1=1   c2=7 N2=0

因为c1g(n)<=c2h(n)  ==> c1g(n)<=c1*c2h(n)

这个时候，我们把c1*c2=c,那么也就是说c1g(n)<=ch(n)  ===>  f(n)<=ch(n)

所以h(n)也就是f(n)的算法时间复杂度。

性质2：如果f(n)=O(h(n))并且g(n)=O(h(n)),那么f(n)+g(n)=O(h(n))

f(n) <= c1h(n),g(n) <= c2h(n)  =>  f(n) + g(n) <= c1h(n) + c2h(n)  =>  f(n) + g(n) <= (c1+c2)h(n)  =>  f(n) + g(n) <= ch(n)   =>  f(n) +g(n) = O(n)

性质3：

函数a*n^k=O(n^k)

要满足不等式a*n^k<=c*n^k  需要令c>=a

性质4：如果f(n)=cg(n),那么f(n)=O(g(n));

这个时候，把N换成刚好相等那个N就可以了，然后推算出一个相应的c值

打个比方

f(n) = 2*n^2 + 3n + 1

g(n) = n^2

要使f(n) = cg(n)的话，那么比如说取1,f(n) = 6 = c * 1 => c= 6,在这种情况下，f(n) = cg(n),当然了，还有无数这样的n与c 的取值，一旦满足上面这个条件，你要想g(n)满足它的时间复杂度的话，你的实际c的取值 >= 使函数相等的c的取值就行

性质5:

先来看一个对数的运算法则

  

常见的函数时间复杂度关系

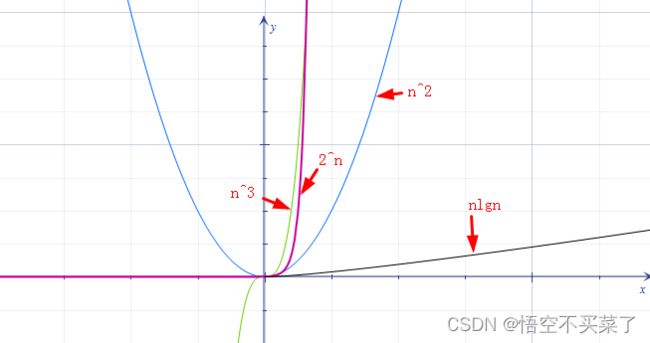
先来看一张函数图

上面就展示了指数函数2^n 与幂函数n^2、n^3还有对数nlgn的函数图像

从图中我们可以明显看出指数函数与幂函数的增长速率是远远大于对数函数的增长的

而2^n、n^3又大于了n^2的增长速率

2^n在某个问题规模下也是超越了n^3的增长速率

所以，总结出如下时间复杂度关系和他们常用于的算法

再来说一点，时间复杂度不代表算法的运行时间，而只是一个算法效率的体现，我们在具体实际程序中，一般通过函数的运行次数来表示这个函数的时间复杂度

 

时间复杂度分析习题讲解

1.

如果一个函数的算法时间复杂度是O(n^2),那么这个函数与大O函数就会形成一个如下关系，f(n) <= cn^2, 也就是执行时间是与n^2成正比的

2.计算时间复杂度 

上面这个算法我们先来看i，每次i的增长都是i=i*2,也就是说按照倍数级增长，假设程序运行x次结束，那么i的值就变为了2^x,根据程序的结束条件，我们可以得出2^x > n,也就是i > n的时候，程序结束，那么两边取对数  >  ,也就是说， >  => x >  ，所以，次函数的算法时间复杂度是O()

3.计算时间复杂度

这很明显是一个斐波拉契数列递归求和，最上层依赖于下层的返回，比如n=3,那么就是3*f(2),又进入一个递归2*f(1),然后又进入f(1),此时就开始返回，然后一层一层的结束 ，这个就和数据规模直接正相关，所以，时间复杂度就是O(n)

4.计算时间复杂度

 可以这样理解，存在如下事实，当i=0 -> i^3 = 0; 当i=1->i^3 = 1;当i=2->i^3 = 8,依次类推，现在假设程序运行x次结束，也就是说x^3 > n  =>   >   =>  >  =>  > ,这里把常数项忽略不计，也就是x > n,所以算法的时间复杂度就是O(n)

5.分析如下算法的时间复杂度

 

对于上面来说，循环次数的关键判断还是在于i的每一次数值的改变，很明显就是一个简单的i++，i > = n-1时程序结束，所以，时间复杂度也就是O(n)

好了，说到这，祝早安，午安，晚安。