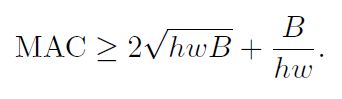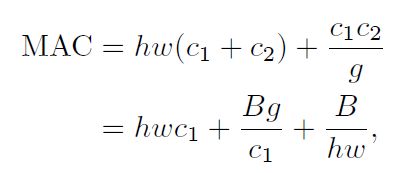ShuffleNet v2
论文 https://arxiv.org/abs/1807.11164
目录
Introduction
四条高效网络设计准则
G1) Equal channel width minimizes memory access cost (MAC)
G2) Excessive group convolution increases MAC
G3) Network fragmentation reduces degree of parallelism
G4) Element-wise operations are non-negnigible
结论
ShuffleNet v2
Introduction
论文首先指出之前的文章在衡量模型复杂度时大多使用FLOPs作为评价指标,但是和速度、延迟这些我们真正在意的指标相比,FLOPs只能作为一个近似,比如MobileNet v2和NASNET-A的FLOPs差不多,但是前者的速度要快得多。
评价指标FLOPs和速度之间的差异主要有两方面的原因,一是一些对速度有很大影响的因素在计算FLOPs时却并没有考虑到,例如内存访问成本MAC(memory access cost)和并行度(degree of parallelism);二是相同FLOPs的操作在不同的平台上速度也不同。
因此作者提出了两条网络执行效率对比的准则
- 使用直接指标如速度而不是间接指标如FLOPs
- 在同一平台上进行评估
四条高效网络设计准则
作者从不同的方面对模型的速度进行了细致的分析,最终得到了4条高效网络的设计准则,具体如下。
G1) Equal channel width minimizes memory access cost (MAC)
即卷积的输入输出channel相同时,内存访问成本最低。
之前的轻量模型通常会使用深度可分离卷积(depthwise separable convolution),其中逐点卷积(pointwise convolution)又占了计算量的大头,假设输入特征图的尺寸为h×w,输入通道数为c1,输出通道数为c2,则1×1卷积的FLOPs为B=hwc1c2。假设平台的缓存足够大可以存储所有的特征图和参数,则内存访问成本MAC=hw(c1+c2)+c1c2,分别代表输入特征图、输出特征图、权重的内存访问成本。根据均值不等式有
因此在给定FLOPs的情况下MAC是有最小值的,且仅当c1=c2时取得最小值。当然这只是理论上的结论,实际上很多设备上的缓存不够大,而且现代的计算库通常采用复杂的阻塞策略来充分利用缓存机制。因此作者做了一系列实验来验证上述结论,通过堆叠10个block,每个block由两个卷积层组成,c1和c2分别是输入和输出通道数,来测试模型推导速度,结果如下
可以看出当c1=c2时,速度最快。随着c1/c2越来越大,速度越来越慢。
G2) Excessive group convolution increases MAC
即过多的组卷积会增大内存访问成本。
组卷积通过只对输入通道的一部分进行卷积减小了FLOPs,因此在FLOPs固定的情况下可以使用更多的通道,从而增加网络容量得到更高的精度。但同时,更多的通道也就意味着MAC的增加。
其中g是分组个数,B=hwc1c2/g是FLOPs。从公式中可以看出,当输入大小c1×h×w和计算成本B固定时,MAC随着g的增加而增加。作者也通过实验论证了上述结论
G3) Network fragmentation reduces degree of parallelism
即网络的分支结构会降低并行度。
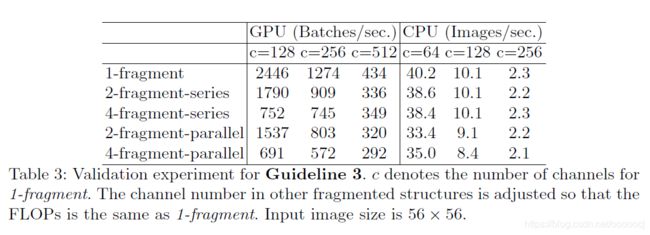
对于像GoogLeNet中用到的并行结构有助于提升精度,但因为对像GPU这样并行计算能力强的设备不友好而降低效率。作者通过实验按串行、并行两种方式组合不同的卷积来评估模型速度,block的结构如下所示
结果如下
可以看出,在FLOPs固定的情况下卷积以串行方式组合时速度更快。
G4) Element-wise operations are non-negnigible
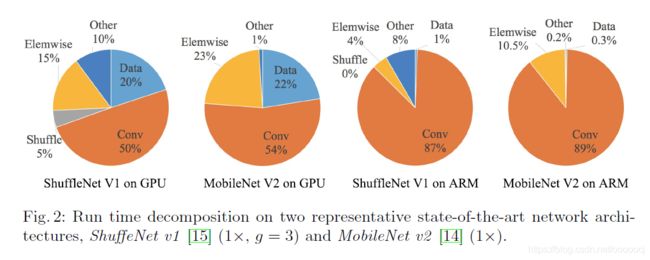
即element-wise操作对速度的影响不应忽略。
如上图所示,element-wise操作还是占据了相当比例的运行时间的,尤其是在GPU上。Element-wise操作包括ReLU、AddTensor、AddBias等,这些操作的FLOPs较小但MAC较大。需要注意的是,我们把深度卷积也看做element-wise操作,因为它的MAC/FLOPs比值很大。
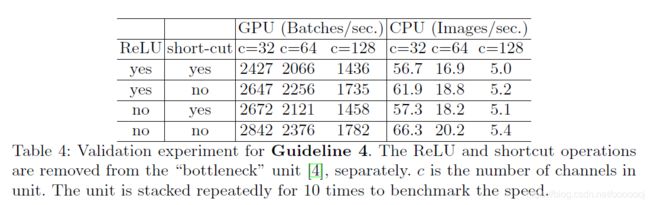
作者同样通过实验进行了验证,以ResNet中的bottleneck为例,通过分别去除ReLU和shortcut来测试速度。
可以看出去除ReLU和shortcut后速度获得了大约20%的提升。
结论
通过以上四个实验,作者总结一个高效的网络结构应该
- use "balanced" convolutions (equal channel width)
- be aware of the cost of using group convolutions
- reduce the degree of fragmentation
- reduce element-wise eperations
ShuffleNet v2
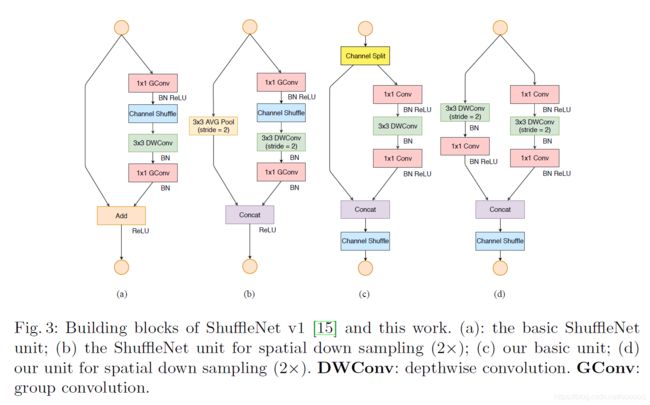
作者按照上述四条准则对shufflenet v1进行了改进,得到了shufflenet v2。v1和v2的block结构如下
作者提出Channel Split操作,如上图(c)所示,在每个单元的开始,输入通道数c被分成c-c'和c'两个分支。按照G3,一个分支保持不变,另一个分支由三个卷积串行组成并且输出和输入通道c'相等,这满足了G1。其中的两个1×1卷积是普通卷积,而不是v1中的组卷积,这一方面是因为G2,另一方面是因为channel split已经算是变相的分组了。
然后两个分支进行Concat,使得整个单元的输出通道和输入通道数c一样(G1)。然后再进行channel shuffle,保证两个分支的信息流动。
shuffling完这个单元就结束了,后面接下一个单元。注意到v1中的Add被去掉了。像ReLU、深度卷积这样的element-wise操作只存在于一个分支中。此外,三个连续的element-wise操作concat、channel shuffle、channel split被组合成一个element-wise操作,这符合G4。
当stride=2时,去掉了channel split,因此最终的输出通道数会double。
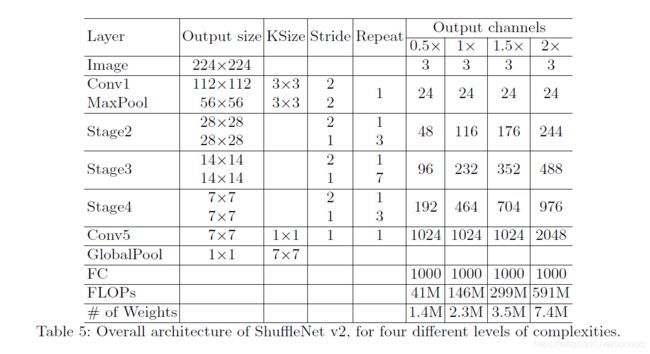
ShuffleNet v2的完整结构如下所示
整体结构和v1类似,只有一点不同,在最后的全局平均池化前加了一层1×1卷积。