Numpy---ndarray矩阵运算、广播机制、排序、文件操作
1. 矩阵运算
n + 10 # 加
n - 10 # 减
n * 10 # 乘
n / 10 # 除
n // 2 # 整除
n ** 2 # 次方
n % 2 # 余数n1 = np.random.randint(0, 10, size=(4, 5))
n2 = np.random.randint(0, 10, size=(4, 5))
display(n1, n2)
array([[3, 6, 1, 9, 9],
[8, 9, 2, 0, 4],
[4, 8, 5, 0, 1],
[6, 1, 0, 0, 9]])
array([[0, 7, 5, 7, 1],
[8, 8, 9, 9, 9],
[2, 6, 4, 2, 9],
[3, 6, 8, 5, 3]])
n1 + n2
n1 * n2
array([[ 0, 42, 5, 63, 9],
[64, 72, 18, 0, 36],
[ 8, 48, 20, 0, 9],
[18, 6, 0, 0, 27]])矩阵积 np.dot():第一个矩阵的列数等于第二个矩阵的行数
n1 = np.random.randint(0, 5, size=(2, 3))
n2 = np.random.randint(0, 5, size=(3, 2))
display(n1, n2)
array([[4, 3, 4],
[1, 2, 4]])
array([[4, 3],
[4, 4],
[0, 4]])
np.dot(n1, n2)
array([[28, 40],
[12, 27]])np.matmul 和 np.dot 的区别: 二者都是矩阵乘法。 np.matmul 中禁止矩阵与标量的乘法。 在矢量
乘矢量的內积运算中,np.matmul 与 np.dot 没有区别。
线性代数中其他矩阵操作:
n = np.array([[1, 2, 3],
[2, 5, 4],
[4, 5, 8]])
# 矩阵逆
np.linalg.inv(n)
# 矩阵的行列式
np.round(np.linalg.det(n))
# 行列式计算: 矩阵的所有主对角线-所有副对角线
# 1*5*8 + 2*4*4 + 3*2*5 - (3*5*4 +2*2*8 + 1*4*5 ) = -10
# 矩阵的秩 (满秩矩阵,奇异矩阵)
# 方阵
np.linalg.matrix_rank(n)其他常见的数学操作:
n = np.array([1, 4, 8, 9, 16, 25, 64])
np.abs(n) # 绝对值
np.sqrt(n) # 平方根
# n ** 0.5
np.square(n) # 平方
# n ** 2
np.exp(n) # 指数 e=2.718281828459045
np.log(n) # 自然对数:以e为底的对数, ln3
np.log(np.e) # 1
np.log(1) # 0
np.log2(n) # 2为底的对数
np.log10(n) # 10为底的对数,常用对数
np.sin(n) # 正弦
np.cos(n) # 余弦
np.tan(n) # 正切
np.round(n, 2) # 四舍五入
np.ceil(n) # 向上取整
np.floor(n) # 向下取整
np.cumsum(n) # 累加
# [1, 4, 8, 9, 16, 25, 64]
# [1, 5,13, 22, 38, 63, 127]2. 广播机制
数组在进行矢量化运算时,要求数组的形状是相等的。当形状不相等的数组执行算术运算的时候,
就会出现广播机制,该机制会对数组进行扩 展,使数组的shape属性值一样,这样,就可以进行矢
量化运算了。
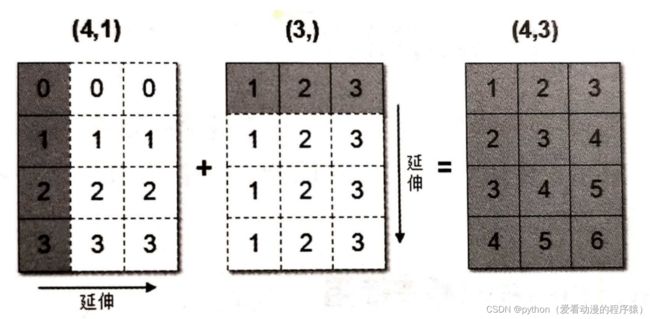
arr1 = np.array([[0],[1],[2],[3]])
arr1.shape
# (4, 1)
arr2 = np.array([1,2,3])
arr2.shape
# (3,)
arr1+arr2
# 结果是:
array([[1, 2, 3],
[2, 3, 4],
[3, 4, 5],
[4, 5, 6]])数组arr1是4行1列,arr2是1行3列。这两个数组要进行相加,按照广播机制会对数组arr1和arr2都
进行扩展,使得数组arr1和arr2 都变成4行3列。
广播机制实现了使两个或两个以上数组的运算,即使这些数组的shape不是完全相同的,只需要满
足如下任意一个条件即可:
如果两个数组的后缘维度(trailing dimension,即从末尾开始算起的维度)的轴长度相符,或其中
的一方的长度为1。
广播会在缺失和(或)长度为1的维度上进行。
广播机制需要扩展维度小的数组,使得它与维度最大的数组的shape值相同,以便使用元素级函数
或者运算符进行运算。
3. 排序
np.sort() 与 ndarray.sort() 都可以,但有区别:
np.sort() 不改变输入;
ndarray.sort() 本地处理,不占用空间,但改变输入。
n1 = np.random.randint(0, 10, size=6)
n1
array([9, 9, 7, 5, 6, 4])
# 不改变原数组
n2 = np.sort(n1)
n2
array([4, 5, 6, 7, 9, 9])
n1
array([9, 9, 7, 5, 6, 4])
n3 = np.random.randint(0, 10, size=6)
n3
array([9, 3, 1, 1, 9, 0])
n3.sort()
n3
array([0, 1, 1, 3, 9, 9])
4. 文件操作
保存数组:
save : 保存ndarray到一个npy文件
savez : 将多个array保存到一个npz文件中
x = np.arange(5)
y = np.arange(10, 20)
# save: 保存x.npy
np.save('x', x)
# savez
np.savez('arr.npz', xarr=x, yarr=y)读取数组:
# 读取npy文件
np.load('x.npy')
# 读取npz文件
np.load('arr.npz')['xarr']csv、txt文件的读写操作:
n = np.random.randint(0, 10, size=(3, 4))
n
array([[4, 6, 6, 0],
[1, 9, 7, 0],
[7, 7, 7, 5]])
# 存储到csv或txt
# delimiter=',': 分隔符
np.savetxt('arr.csv', n, delimiter=',')
# 读取csv或txt
np.loadtxt('arr.csv', delimiter=',', dtype=np.int16)
array([[4, 6, 6, 0],
[1, 9, 7, 0],
[7, 7, 7, 5]], dtype=int16)array([[4, 6, 6, 0],
[1, 9, 7, 0],
[7, 7, 7, 5]], dtype=int16)