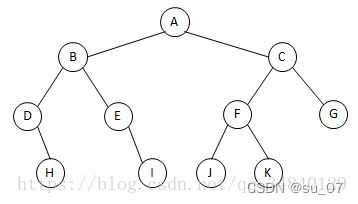
求解二叉树

二叉树的三种遍历方式：

1.先序遍历：按照根节点->左子树->右子树的顺序访问二叉树

A B D H E I C F J K G

2.中序遍历：按照左子树->根节点->右子树的顺序访问

D H B E I A J F K C G

3.后序遍历：按照左子树->右子树–>根节点的顺序访问

H D I E B J K F G C A

求解二叉树

1.已知：中序遍历序列、前序遍历序列

1 2 3 4 5 6 7
4 1 3 2 6 5 7

#include
using namespace std;
struct ss{
    ss *Left;
    ss *Right;
    int data;
};
int n, a[50], b[50], h;
ss *dss(int a[], int b[], int n){
    if(n <= 0) 
        return NULL;
    ss *T = new ss();
    int root = a[0]; //找到根节点
    int k = -1;
    T->data = root; //创建树的节点
    for(int i = 0; i < n; i ++){ //由于中序遍历使两边分开
        if(b[i] == root){
            k = i;
            break;
        }
    }
    T->Left = dss(a+1,b,k);
    T->Right = dss(a+k+1,b+k+1,n-(k+1));
    return T;
}
void p(ss *T){
    cout << T->data << " ";
    if(T->Left != NULL)
        p(T->Left);
    if(T->Right != NULL)
        p(T->Right);
}
int main()
{
	cin >> n;
    for(int i = 0; i < n; i ++){ // 前
        cin >> a[i];
    }
    for(int i = 0; i < n; i ++){ // 中
        cin >> b[i];
    }
    ss *T = dss(a,b,n);
    p(T);
	return 0;
}

2.已知：中序遍历序列、后序遍历序列

1 2 3 4 5 6 7
2 3 1 5 7 6 4

#include
using namespace std;
struct ss{
    ss *Left;
    ss *Right;
    int data;
};
int n, a[50], b[50], h;
ss *dss(int a[], int b[], int n){
    if(n <= 0) 
        return NULL;
    ss *T = new ss();
    int root = a[n-1]; //找到根节点
    int k = -1;
    T->data = root; //创建树的节点
    for(int i = 0; i < n; i ++){ //由于中序遍历使两边分开
        if(b[i] == root){
            k = i;
            break;
        }
    }
    T->Left = dss(a,b,k);
    T->Right = dss(a+k,b+k+1,n-(k+1));
    return T;
}
void p(ss *T){
    cout << T->data << " ";
    if(T->Left != NULL)
        p(T->Left);
    if(T->Right != NULL)
        p(T->Right);
}
int main()
{
	cin >> n;
    for(int i = 0; i < n; i ++){ // 后
        cin >> a[i];
    }
    for(int i = 0; i < n; i ++){ // 中
        cin >> b[i];
    }
    ss *T = dss(a,b,n);
    p(T);
	return 0;
}

1、2对比：

// 已知中前
int root = a[0]; // 找到根节点
T->Left = dss(a+1,b,k); // 左遍历
T->Right = dss(a+k+1,b+k+1,n-(k+1)); // 右遍历
// 已知中后
int root = a[n-1]; // 找到根节点
T->Left = dss(a,b,k); // 左遍历
T->Right = dss(a+k,b+k+1,n-(k+1)); // 右遍历

层次遍历：

void print(ss *T)//层次遍历输出二叉树
{
  ss *p;//为中间变量
  ss *pr[100];
  int rear = -1, front = -1, num = 0;
  rear ++;
  pr[rear] = T;//将根节点放入到队列之中
  while(rear != front){
      front ++;
      p = pr[front]; //用来读取数据
      cout << p->data;
      num ++; //用来控制空格的输出，最后一位不用空格
      if(num < n)
         cout<<" ";
      if(p->Left){
          rear ++;
          pr[rear] = p->Left;
      }
       if(p->Right){
          rear ++;
          pr[rear] = p->Right;
      }
  }
}