熵权法求权重
熵权法求权重
-
- 创作背景
- 知识补充
-
- 熵
- 熵权法求权重过程
-
- 一、特征缩放
-
- 归一化
- 标准化
- 注
- 二、求熵
- 三、求权重
- 实战
-
- 一、特征缩放
- 二、求各特征的熵
- 三、求个特征权重
- 结尾
创作背景
最近本菜鸡在帮别人搞个 熵权法求权重 ,给的数据是差不多 5 份打分表,有字段和对应的打分,要我求一下 每个字段对应的权重 ,对于这点小忙我还是很乐意帮的,本片博客就用来记录一下过程。
如果觉得我这篇文章写的好的话,能不能给我 点个赞 ,评论 一波。
如果要点个 关注 的话也不是不可以。
知识补充
让我们了解一下熵权法,参考 这篇文章 。
熵
既然是要根据 熵 来求权重,我们也得知道 熵 是什么。
熵 是 统计物理与信息论术语 ,泛指某些 物质系统状态的 一种 量度,某些物质系统状态可能出现的程度。系统 越混乱 ,熵越大 。
假定 P ( x = x i ) = p i P(x=x_i)=p_i P(x=xi)=pi,则 熵 公式如下:
H ( x ) = − ∑ i = 1 n p i log n p i H(x)=- \sum^{n}_{i=1}{p_i \log_{n}{p_i}} H(x)=−i=1∑npilognpi
其中 n 代表分类问题中 类别个数 。
而 多分类 问题可以转化为 多个二分类 问题。
假设特征 A 取值 X ∈ X 1 , X 2 , … , X i X \in {X_1, X_2, \dots ,X_i} X∈X1,X2,…,Xi ,每个特征概率取值 p i = X i ∑ j = 1 n X j p_i=\frac{X_i}{\displaystyle \sum^{n}_{j=1}{Xj}} pi=j=1∑nXjXi ,则二分类的 熵 公式如下:
H ( x ) = − p i log 2 p i − ( 1 − p ) log 2 ( 1 − p i ) H(x)=- p_i \log_{2}{p_i} - (1-p) \log_{2}{(1-p_i)} H(x)=−pilog2pi−(1−p)log2(1−pi)
其中, p i = ∈ ( 0 , 1 ) p_i= \in (0, 1) pi=∈(0,1) 。
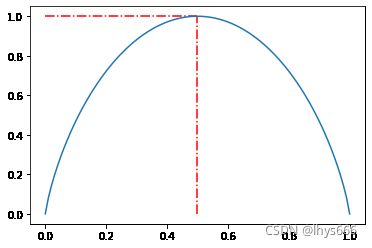
- p i = 1 o r 0 p_i = 1 \: or \: 0 pi=1or0 时, H ( x ) = 0 H(x)=0 H(x)=0 。
- p i = 1 2 p_i = \frac{1}{2} pi=21 时, H ( x ) = 1 H(x)=1 H(x)=1 。
图像如下
熵权法求权重过程
这是本篇文章主要部分。
输入数据是 已经过数据预处理的训练数据 。
熵权法求权重 分为以下几步:
- 对各特征数据进行 特征缩放 ,目的是:将数据都转换为化为无量纲数据 。
- 求各特征对应的 熵 ,目的是:求权 。
- 求各特征所对应的 权重 。
一、特征缩放
特征缩放一般有两种方法:归一化 和 标准化 。
归一化
公式如下:
x ′ = x − X m i n X m a x − X m i n x' = \frac{x-{X}_{min}}{{X}_{max}-{X}_{min}} x′=Xmax−Xminx−Xmin
就是将原数据 [ X m i n , X m a x ] [{X}_{min}, {X}_{max}] [Xmin,Xmax] 这个区间缩放到 [ 0 , 1 ] [0, 1] [0,1] 区间内。
缺点:当 数据发生变化(增加、删除、修改) 时,最大值和最小值 会发生变化,需要 重新计算 。
标准化
公式如下:
x ′ = x − μ σ x' = \frac{x-\mu}{\sigma} x′=σx−μ
其中, μ \mu μ 和 σ \sigma σ 分别代表数据的 均值 和 方差 。
注
这里每种特征缩放方法只列举了 一个公式 ,而实际上二者都有 多个公式 ,感兴趣的朋友可以自行百度。
二、求熵
使用上述 熵 的公式,即:
H ( x ) = − ∑ i = 1 n p i log n p i H(x)=- \sum^{n}_{i=1}{p_i \log_{n}{p_i}} H(x)=−i=1∑npilognpi
三、求权重
公式如下:
W i = 1 − E i k − ∑ E i W_i=\frac{1-E_i}{k- \sum{E_i}} Wi=k−∑Ei1−Ei
其中,k 代表 特征个数 。
这就求出了各特征对应的权重。
实战
假设数据如下:
| Aa1 | Aa2 | Aa3 | Aa4 | Ab1 | Ab2 | Ba1 | Ba2 | Bb1 | Bb2 | Bc1 | Bc2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 3 | 5 | 5 | 5 | 3 | 1 | 4 | 4 | 4 | 4 |
| 2 | 3 | 2 | 4 | 3 | 2 | 1 | 2 | 3 | 3 | 4 | 4 |
| 5 | 4 | 2 | 4 | 5 | 4 | 4 | 3 | 5 | 5 | 4 | 3 |
| 5 | 4 | 3 | 3 | 2 | 2 | 3 | 2 | 2 | 3 | 2 | 5 |
| 5 | 3 | 3 | 3 | 5 | 5 | 4 | 2 | 3 | 5 | 5 | 3 |
其中,Aa1 到 Bc2 为各个特征,每个特征有 5 条数据,取值在 [0, 5] ,下面我们就要对各个特征求其所对应的权重。
一、特征缩放
这里我选用 归一化 。代码如下:
def scale(data):
return (data - data.min()) / (data.max() - data.min())
data = data.apply(scale)
data
结果如下:
| Aa1 | Aa2 | Aa3 | Aa4 | Ab1 | Ab2 | Ba1 | Ba2 | Bb1 | Bb2 | Bc1 | Bc2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.333333 | 1.0 | 1.0 | 1.0 | 1.000000 | 1.000000 | 0.666667 | 0.0 | 0.666667 | 0.5 | 0.666667 | 0.5 |
| 1 | 0.000000 | 0.0 | 0.0 | 0.5 | 0.333333 | 0.000000 | 0.000000 | 0.5 | 0.333333 | 0.0 | 0.666667 | 0.5 |
| 2 | 1.000000 | 1.0 | 0.0 | 0.5 | 1.000000 | 0.666667 | 1.000000 | 1.0 | 1.000000 | 1.0 | 0.666667 | 0.0 |
| 3 | 1.000000 | 1.0 | 1.0 | 0.0 | 0.000000 | 0.000000 | 0.666667 | 0.5 | 0.000000 | 0.0 | 0.000000 | 1.0 |
| 4 | 1.000000 | 0.0 | 1.0 | 0.0 | 1.000000 | 1.000000 | 1.000000 | 0.5 | 0.333333 | 1.0 | 1.000000 | 0.0 |
二、求各特征的熵
代码如下:
In[]: def get_entropy(data):
data = data.map(lambda x: x / data.sum())
return -1 / np.log(data.size) * data.map(lambda x: x * np.log(x)).sum()
data = data.apply(get_entropy)
data.name = 'entropy'
data
---------------------------------------------------------------------
Out[]: Aa1 0.816331
Aa2 0.682606
Aa3 0.682606
Aa4 0.646015
Ab1 0.816331
Ab2 0.672406
Ba1 0.848842
Ba2 0.827729
Bb1 0.793466
Bb2 0.655459
Bc1 0.850559
Bc2 0.646015
Name: entropy, dtype: float64
三、求个特征权重
In[]: def keep_weight(entropy_s):
return entropy_s.map(lambda x: (1-x) / (entropy_s.size-entropy_s.sum()))
weight_s = keep_weight(data)
weight_s.name = 'weight'
weight_s
---------------------------------------------------------------------
Out[]: Aa1 0.059991
Aa2 0.103668
Aa3 0.103668
Aa4 0.115620
Ab1 0.059991
Ab2 0.107000
Ba1 0.049372
Ba2 0.056268
Bb1 0.067459
Bb2 0.112535
Bc1 0.048811
Bc2 0.115620
Name: weight, dtype: float64
看一下权重之和:
In[]: weight_s.sum()
---------------------------------------------------------------------
Out[]: 1.0
刚刚好。完成任务~~~
结尾
有想要一起学习 python 的小伙伴可以 私信我 进群哦。
以上就是我要分享的内容,因为学识尚浅,会有不足,还请各位大佬指正。
有什么问题也可在评论区留言。
![]()