数学模型：Python实现线性规划

文章摘要：线性规划的Python实现。
参考书籍：数学建模算法与应用(第3版)司守奎 孙玺菁。
PS：只涉及了具体实现并不涉及底层理论。学习底层理论以及底层理论实现：可以参考1.最优化模型与算法——基于Python实现 渐令 粱锡军2.算法导论(原书第3版)Thomas H.Cormen Charles E.Leiserson、Ronald L.Rivest Clifford Stein
文章声明：如有发现错误，还望批评指正。

线性规划简述

目标函数：
$\max or\min y=\sum _{i=1}^n{a}_i{x}_i$

约束条件：
$\sum _{j=1}^n{a}_{ij}{x}_j\le or=or\ge b_i,i=1,2,\dots ,m$
$x_j\ge 0，j=1,2,\dots ,n$

一些名词： 可行解，可行域与最优解。

PS：至于如何找到最优解的还请参考最前面的PS，没有兴趣可以不用进行研究。希望以后上了最优化的课程或者有时间了能够手搓。感觉工程量有点大，哈哈也许没有必要。所以博主没有学习过最优化相关理论，对于求解器的方法同样也不知道。但是从工程的角度，我们可以不用知道，那是理论学家需要去做的事。看需要，看兴趣。

线性规划实现

参考书籍例1.9
目标函数：
$\max \sum _{i=0}^n(r_i-p_i)x_i$
$\min \{\underset{1\le i\le n}{\max }\{q_i{x}_i\}\}$
约束条件：
$\sum _{i=0}^n(1+p_i)x_i=M$
$x_i\ge 0,i=0,1,2,\dots ,n$

模型一：固定风险，最大收益

目标函数：
$\max \sum _{i=0}^n(r_i-p_i)x_i$
约束条件：
$\frac{q_i{x}_i}{M}\le a,i=0,1,2,\dots ,n$
$\sum _{i=0}^n(1+p_i)x_i=M$
$x_i\ge 0,i=0,1,2,\dots ,n$

from scipy.optimize import linprog
import numpy  as np
M=10000
lt1=np.array([0.05,0.28,0.21,0.23,0.25])
lt2=np.array([0,0.01,0.02,0.045,0.065])
c=lt1-lt2;c=-c
A_ub1=np.diag([0,0.025,0.015,0.055,0.026]);A_ub2=np.diag([-1,-1,-1,-1,-1]);A_ub=np.vstack((A_ub1,A_ub2))
A_eq=1+lt2;A_eq=A_eq.reshape(1,-1)
b_eq=np.array([M])
lt=[]
for i in range(0,50):
    b_ub=np.array([i/1000*M for _ in range(5)]+[0 for _ in range(5)])
    result=linprog(c,A_ub,b_ub,A_eq,b_eq)
    lt.append(-result.fun)
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(16,9));sns.set_style("darkgrid");plt.rcParams['font.sans-serif']=['SimHei']
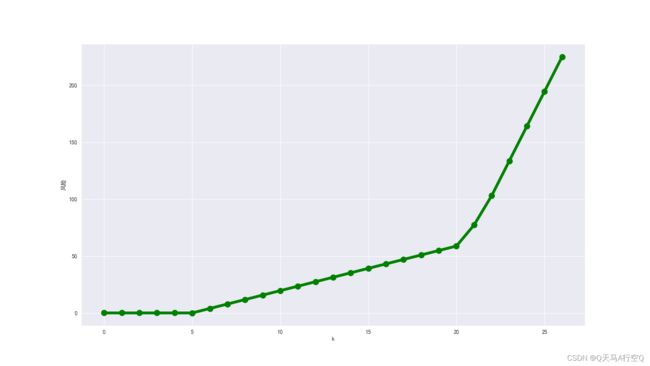
plt.plot([i for i in range(len(lt))],lt,ms=10,marker="o",linestyle="--",linewidth=5,color="green")
plt.xlabel("a");plt.ylabel("收益");plt.show()

以下两个模型需要目标函数进行线性转换。但是这样会造成不等式约束右侧包含变量，scipy库无法解决所以使用cvxpy库(至少我没找功能函数)。

模型二：固定收益，最小风险

目标函数：
$\min \{\underset{1\le i\le n}{\max }\{q_i{x}_i\}\}$
约束条件：
$\sum _{i=0}^n(r_i-p_i)x_i\ge kM$
$\sum _{i=0}^n(1+p_i)x_i=M$
$x_i\ge 0,i=0,1,2\dots ,n$

import numpy as np
import cvxpy as cp
M=10000
x=cp.Variable(6,pos=True)
obj=cp.Minimize(x[5])
p=np.array([0,0.01,0.02,0.045,0.065])
con1=(1+p)@x[:-1]==M
q=np.array([0,0.025,0.015,0.055,0.026])
con2=cp.multiply(q,x[:5])<=x[5]
r=np.array([0.05,0.28,0.21,0.23,0.25])
lt=[]
for i in range(100):
    con3=(r-p)@x[:-1]>=i/100*M
    con=[con1,con2,con3]
    pro=cp.Problem(obj,con)
    pro.solve(solver='ECOS')
    lt.append(x.value[5])
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(16,9));sns.set_style("darkgrid");plt.rcParams['font.sans-serif']=['SimHei']
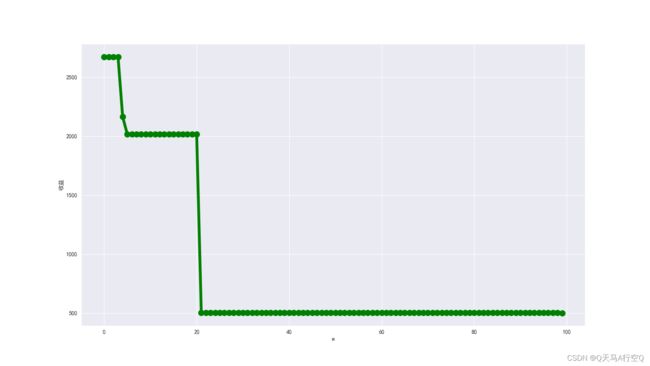
plt.plot([i for i in range(len(lt))],lt,ms=10,marker="o",linewidth=5,color="green")
plt.xlabel("k");plt.ylabel("风险");plt.savefig("figure")

分析：收益到0.26之后便就没有解了。
注释：(默认问题为凸问题，具体是不是我证明不了)ECOS是一个求解凸优化的方法(具体理论我不知道)，具有数值稳定，求解效率等等优点，

模型三：目标函数加权求和

目标函数：
$\min \{\omega \{\underset{1\le i\le n}{\max }\{q_i{x}_i\}\}-(1-\omega )\sum _{i=0}^n(r_i-p_i)x_i$}
约束条件：
$\sum _{i=0}^n(1+p_i)x_i=M$
$x_i\ge 0,i=0,1,2,\dots ,n$

import numpy as np
import cvxpy as cp
M=10000
x=cp.Variable(6,pos=True)
p=np.array([0,0.01,0.02,0.045,0.065])
con1=(1+p)@x[:-1]==M
q=np.array([0,0.025,0.015,0.055,0.026])
con2=cp.multiply(q,x[:5])<=x[5]
con=[con1,con2]
r=np.array([0.05,0.28,0.21,0.23,0.25])
lt1=[];lt2=[]
for i in range(100):
    obj=cp.Minimize(i*x[5]-(1-i/100)*((r-p)@x[:-1]))
    pro=cp.Problem(obj,con);pro.solve(solver='ECOS')
    lt1.append((r-p)@x.value[:-1]);lt2.append(x[5].value)
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(16,9));sns.set_style("darkgrid");plt.rcParams['font.sans-serif']=['SimHei']
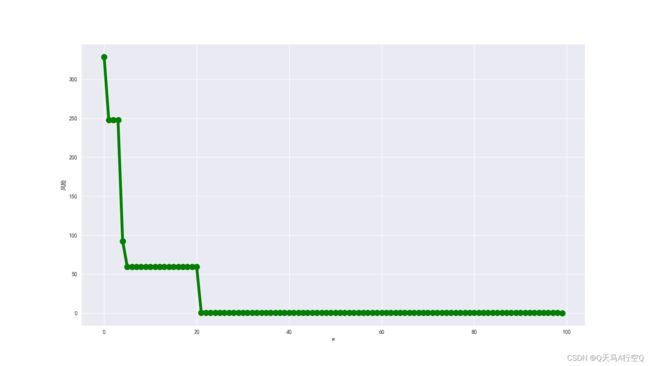
plt.plot([i for i in range(len(lt1))],lt1,ms=10,marker="o",linewidth=5,color="green")
plt.xlabel("w");plt.ylabel("收益");plt.savefig("figure1")
plt.figure(figsize=(16,9));sns.set_style("darkgrid");plt.rcParams['font.sans-serif']=['SimHei']
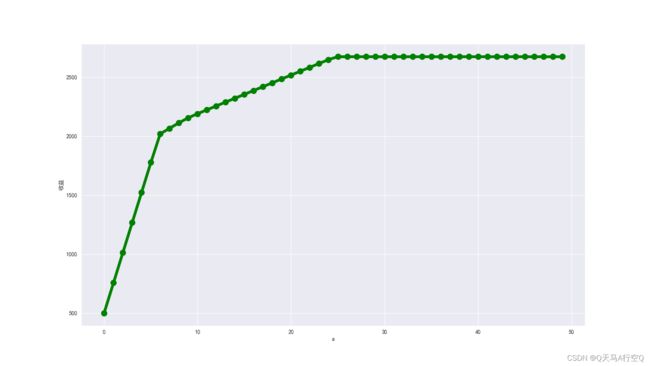
plt.plot([i for i in range(len(lt2))],lt2,ms=10,marker="o",linewidth=5,color="green")
plt.xlabel("w");plt.ylabel("风险");plt.savefig("figure2")

下篇文章：整数规划