频域抽取FFT(DIF-FFT)的C语言实现

原理

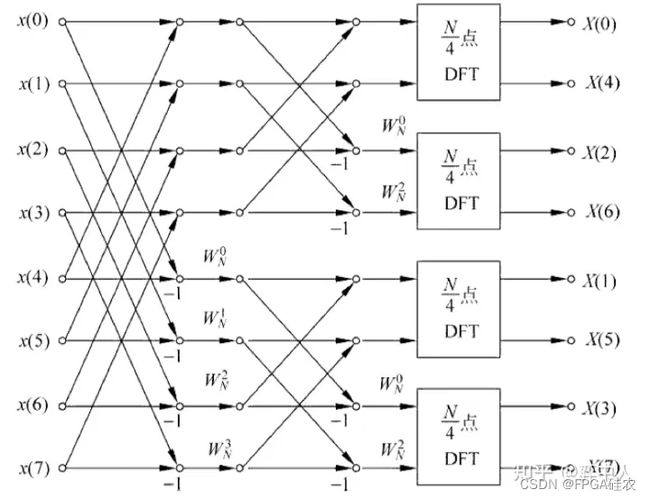
此处以基2频域抽取FFT为例，讲述频域抽取FFT的原理。假设FFT的长度为$N=2^m$，我们将序列$x$的FFT变换分为以下两个部分：
$$X(k)=\sum _{n=0}^{N/2-1}x(n)W_N^{nk}+\sum _{n=N/2}^{N-1}x(n)W_N^{nk}$$
对等号右边的第二项作代换：$n=n+N/2$，则有：
$$X(k)=\sum _{n=0}^{N/2-1}x(n)W_N^{nk}+\sum _{n=0}^{N/2-1}x(n+N/2)W_N^{k(n+N/2)}$$
由于$W_N^{k(n+N/2)}=W_N^{kn}\cdot W_N^{kN/2}=(-1{)}^k{W}_N^{nk}$，故有：
$$X(k)=\sum _{n=0}^{N/2-1}x(n)W_N^{nk}+(-1{)}^k\sum _{n=0}^{N/2-1}x(n+N/2)W_N^{kn}$$
令$k=2m$以及$k=2m+1$,分别有：
$$X(2m)=\sum _{n=0}^{N/2-1}(x(n)+x(n+N/2))W_N^{2nm}$$
$$X(2m+1)=\sum _{n=0}^{N/2-1}(x(n)-x(n+N/2))W_N^{n(2m+1)}$$
根据旋转因子$W_N$的可约性，有：
$$X(2m)=\sum _{n=0}^{N/2-1}(x(n)+x(n+N/2))W_{N/2}^{nm}$$
$$X(2m+1)=\sum _{m=0}^{N/2-1}(x(n)-x(n+N/2))W_N^n\cdot W_{N/2}^{nm}$$
令$x_1(n)=x(n)+x(n+N/2),x_2(n)=(x(n)-x(n+N/2))W_N^n$，则上式可以写作：
$$X(2m)=\sum _{n=0}^{N/2-1}{x}_1(n)W_{N/2}^{nm}$$
$$X(2m+1)=\sum _{n=0}^{N/2-1}{x}_2(n)W_{N/2}^{nm}$$
由此，我们将N点FFT转换为了两个N/2点的FFT，这就是FFT中分而治之的思想。

下图是8点频域抽取FFT的蝶形运算示意图：

实现

#include
#include
#include
#define PI 3.14159

using namespace std;
typedef complex<double> cdata_t;

void FFT(complex<double>* Xin,complex<double> *Xout,int N){
    if(N<2)
         Xout[0]=Xin[0];
    else
    {
         complex<double>* X1=new complex<double>[N/2];
         complex<double>* X2=new complex<double>[N/2];
         complex<double>* X1_out=new complex<double>[N/2];
         complex<double>* X2_out=new complex<double>[N/2];
         for(int i=0;i<N;i+=2)
         {
                X1[i/2]=Xin[i];
                X2[i/2]=Xin[i+1];
         }
         FFT(X1,X1_out,N/2);
         FFT(X2,X2_out,N/2);
         complex<double>* W=new complex<double>[N/2];
         for(int i=0;i<N/2;i++){
            W[i].real(cos(2*PI*i/N));
            W[i].imag(-sin(2*PI*i/N));
         }
         for(int i=0;i<N/2;i++){
                Xout[i]=X1_out[i]+W[i]*X2_out[i];
                Xout[i+N/2]=X1_out[i]-W[i]*X2_out[i];
         }
        delete []X1;
        delete []X2;
        delete []X1_out;
        delete []X2_out;
    }
    return;
}

void DIF_FFT8(complex<double>* Xin,complex<double>* Xout){
    complex<double> W[4];
    complex<double> TMP1[8];
    complex<double> TMP2[8];
    complex<double> TMP3[8];
    const int N=8;
    for(int i=0;i<4;i++){
        W[i]=complex<double>(cos(2*PI*i/N),-sin(2*PI*i/N));
    }
    //stage1
    for(int i=0;i<4;i++){
        TMP1[i]=Xin[i]+Xin[i+4];
        TMP1[i+4]=(Xin[i]-Xin[i+4])*W[i];
    }
    //stage2
    for(int i=0;i<2;i++)
    for(int j=0;j<2;j++){
        TMP2[i*4+j]=TMP1[i*4+j]+TMP1[i*4+j+2];
        TMP2[i*4+j+2]=(TMP1[i*4+j]-TMP1[i*4+j+2])*W[2*j];
    }
    //stage3
    for(int i=0;i<4;i++){
        TMP3[i*2]=TMP2[i*2]+TMP2[i*2+1];
        TMP3[i*2+1]=(TMP2[i*2]-TMP2[i*2+1])*W[0];
    }
    //
    Xout[0]=TMP3[0];
    Xout[1]=TMP3[4];
    Xout[2]=TMP3[2];
    Xout[3]=TMP3[6];
    Xout[4]=TMP3[1];
    Xout[5]=TMP3[5];
    Xout[6]=TMP3[3];
    Xout[7]=TMP3[7];

}

void DIF_FFT16(cdata_t* Xin,cdata_t* Xout){
    cdata_t W[8];
    cdata_t T1[16];
    cdata_t T2[16];
    cdata_t T3[16];
    cdata_t T4[16];
    //
    for(int i=0;i<8;i++){
        W[i]=cdata_t(cos(2*PI*i/16),-sin(2*PI*i/16));
    }
    //stage1
    for(int i=0;i<8;i++)
    {
        T1[i]=Xin[i]+Xin[i+8];
        T1[i+8]=(Xin[i]-Xin[i+8])*W[i];
    }
    //stage2
    for(int i=0;i<2;i++)
    for(int j=0;j<4;j++){
        T2[i*8+j]=T1[i*8+j]+T1[i*8+j+4];
        T2[i*8+j+4]=(T1[i*8+j]-T1[i*8+j+4])*W[2*j];
    }
    //stage3
    for(int i=0;i<4;i++)
    for(int j=0;j<2;j++){
        T3[i*4+j]=T2[i*4+j]+T2[i*4+j+2];
        T3[i*4+j+2]=(T2[i*4+j]-T2[i*4+j+2])*W[4*j];
    }
    //stage4
    for(int i=0;i<8;i++){
        T4[2*i]=T3[2*i]+T3[2*i+1];
        T4[2*i+1]=T3[2*i]-T3[2*i+1];
    }
    //
    Xout[0]=T4[0];
    Xout[1]=T4[8];
    Xout[2]=T4[4];
    Xout[3]=T4[12];
    Xout[4]=T4[2];
    Xout[5]=T4[10];
    Xout[6]=T4[6];
    Xout[7]=T4[14];
    Xout[8]=T4[1];
    Xout[9]=T4[9];
    Xout[10]=T4[5];
    Xout[11]=T4[13];
    Xout[12]=T4[3];
    Xout[13]=T4[11];
    Xout[14]=T4[7];
    Xout[15]=T4[15];
}

void DIF_FFT4(cdata_t* Xin,cdata_t* Xout){
    cdata_t W[2];
    cdata_t T1[4];
    cdata_t T2[4];
    for(int i=0;i<2;i++){
        W[i]=cdata_t(cos(2*PI*i/4),-sin(2*PI*i/4));
    }
    //stage1
    for(int i=0;i<2;i++){
        T1[i]=Xin[i]+Xin[i+2];
        T1[i+2]=(Xin[i]-Xin[i+2])*W[i];
    }
    //stage2
    for(int i=0;i<2;i++){
        T2[i*2]=T1[i*2]+T1[i*2+1];
        T2[i*2+1]=(T1[i*2]-T1[i*2+1]);
    }
    //
    Xout[0]=T2[0];
    Xout[1]=T2[2];
    Xout[2]=T2[1];
    Xout[3]=T2[3];
}

int main(){
    //FFT_LENGTH点傅里叶变换
    int n=4;
    complex<double> X[n];
    complex<double> Y[n];
    complex<double> Y2[n];
    for(int i=0;i<n;i++){
        X[i].real(i);
        X[i].imag(0);
    }
    FFT(X,Y,n);
    if(n==4)
        DIF_FFT4(X,Y2);
    else if(n==8)
        DIF_FFT8(X,Y2);
    else if(n==16)
        DIF_FFT16(X,Y2);
    else
        cout<<"未实现该长度的蝶形FFT函数"<<endl;
    for(int i=0;i<n;i++)
        cout<<Y[i]-Y2[i]<<endl;
    return 0;
}