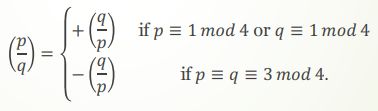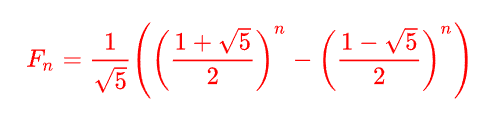数论与组合数学 期末总结(完结)
数论与组合数学
- 自然数的基本性质
- 整除
-
- 最大公约数(GCD)
-
- 辗转相除法=欧几里得算法
- 互质 Coprime
- 素数
- 算数基本定理
- 同余
-
- 欧拉定理
-
- 欧拉函数
- 费马小定理
- 威尔逊定理
- 逆元
-
- 求逆:欧几里得扩展算法
- 线性同余方程组 ( a x = b m o d m ) (ax=b\ mod\ m) (ax=b mod m)
-
- 求线性同余方程组:中国剩余定理
- 高次同余方程组
-
- Hensel引理
- 模多项式
- 阶
- 原根
-
- 原根数量
- 原根存在判定
- 平方剩余
-
- 勒让德符号
- 高斯引理
- 二次互反律 Quadratic Reciprocity Law
- 雅可比符号
- Tonelli-Shanks算法(不考)
- 分圆多项式 Cyclotomic Polynomials
- 算数函数 arithmetic function N->C
- 卷积(不考)
- 连分式 continued fraction
- 基本计数原理
-
- 加法原理
- 乘法原理
- 数学归纳法
- 鸽巢原理
- 容斥原理
- 生成函数
-
- 普通生成函数
- 斐波那契数列
- 指数生成函数(不考)
- 排列与组合
-
- 排列permutation
- 组合 Combination
- 二项式系数
- 多项式系数
- 组成 composition
-
- 分糖果 糖果相同,人不同
- 集合划分 糖果不同,筐子相同
-
- 斯特林第二类数S(n,k)
- 贝尔数
- 整数划分 糖果相同,筐子相同
- 卡特兰数
自然数的基本性质
- 数学归纳法(Principle of Mathematical Induction)
n = n 0 n=n_{0} n=n0时成立,且 n = k n=k n=k成立 ⇒ n = k + 1 \Rightarrow n=k+1 ⇒n=k+1成立,则定理对 n ≥ n 0 n\ge n_{0} n≥n0成立 - 良序定理(Well Ordering Principle)
每个非空集合都存在一个最小元素
整除
定义: a ∣ b a|b a∣b 代表 b = a x ( a , b , x ∈ Z , a ≠ 0 ) b=ax(a,b,x\in Z,a\ne 0) b=ax(a,b,x∈Z,a=0),读作a整除b
性质:
- ∀ n ∈ N , n ∣ 0 \forall n\in N,n|0 ∀n∈N,n∣0
任何自然数可整除0 - a ∣ b , b ∣ c ⇒ a ∣ c a|b,b|c \Rightarrow a|c a∣b,b∣c⇒a∣c
a整除b,b整除c ⇒ \Rightarrow ⇒a整除c - a ∣ b , a ∣ c ⇒ a ∣ b x + c y a|b,a|c \Rightarrow a|bx+cy a∣b,a∣c⇒a∣bx+cy , ∀ x , y ∈ Z \forall x,y\in Z ∀x,y∈Z
a整除b,a整除c ⇒ \Rightarrow ⇒a整除(bx+cy),其中x,y是任意整数
定理:
- a , b ∈ Z , a > 0 , ∃ q , r ∈ Z a,b\in Z,a>0,\exists q,r\in Z a,b∈Z,a>0,∃q,r∈Z,使得 b = a q + r , 0 ≤ r < a b=aq+r,0\le rb=aq+r,0≤r<a
b可以拆成q倍的a+余数的形式,r必须>=0
最大公约数(GCD)
定理
-设 g = g c d ( a , b ) , ∃ x 0 , y 0 ∈ Z g=gcd(a,b),\exist x_0,y_0 \in Z g=gcd(a,b),∃x0,y0∈Z使得 g = a x 0 + b y 0 g=ax_0+by_0 g=ax0+by0
辗转相除法=欧几里得算法
int gcd(int a,int b){
if(a<0)a=-a;
if(b<0)b=-b;
return b==0?a:gcd(b,a%b);
}
互质 Coprime
定义:gcd(a,b)=1,称a,b互质
推论
- g c d ( a , m ) = 1 , g c d ( b , m ) = 1 ⇒ g c d ( a b , m ) = 1 gcd(a,m)=1,gcd(b,m)=1\Rightarrow gcd(ab,m)=1 gcd(a,m)=1,gcd(b,m)=1⇒gcd(ab,m)=1
a,m互质,b,m互质,推出ab和m互质 - c ∣ a b , g c d ( c , a ) = 1 ⇒ c ∣ b c|ab,gcd(c,a)=1\Rightarrow c|b c∣ab,gcd(c,a)=1⇒c∣b
c整除ab,c,a互质,推出c整除b
素数
定义:p(整数p>1)的因子只有1和它本身
算数基本定理
任何正整数都可以被拆分为一系列素数的幂次的乘积,且分解唯一
定理
- 素数的个数无限
素数生成方法: ∏ i = 1 n p i + 1 \textstyle \prod_{i=1}^{n}p_i+1 ∏i=1npi+1
同余
定义: a ≡ b m o d m a\equiv b \ mod\ m a≡b mod m 代表 m ∣ ( a − b ) ( a , b , m ∈ Z , m ≠ 0 ) m|(a-b)\ (a,b,m\in Z,m\ne 0) m∣(a−b) (a,b,m∈Z,m=0)
性质:
当 a ≡ b ( m o d m ) , c ≡ d ( m o d m ) a\equiv b(mod\ m),c\equiv d(mod\ m) a≡b(mod m),c≡d(mod m)时,
- a + c ≡ b + d ( m o d m ) a+c\equiv b+d(mod\ m) a+c≡b+d(mod m)
- a c ≡ b d ( m o d m ) ac\equiv bd(mod\ m) ac≡bd(mod m)
- a k ≡ b k ( m o d m ) a^k\equiv b^k(mod\ m) ak≡bk(mod m)
定义:
完全剩余系:mod m的互不同余的所有数的集合
既约剩余系:mod m的互不同余且和m互质的所有数的集合
欧拉定理
欧拉函数
定义: ϕ ( m ) \phi (m) ϕ(m)代表m的既约剩余系的元素个数
- 对于素数来说,这个函数的结果是m-1
- p是素数,k>=1,则 ϕ ( p k ) = p k − p k − 1 = p k ( 1 − 1 p ) \phi(p^k)=p^k-p^{k-1}=p^k(1-\frac{1}{p}) ϕ(pk)=pk−pk−1=pk(1−p1)
- m,n互质 ϕ ( m n ) = ϕ ( m ) ϕ ( n ) \phi(mn)=\phi(m)\phi(n) ϕ(mn)=ϕ(m)ϕ(n)
- n可用算术基本定理拆开, ϕ ( n ) = n ∏ p ∣ n ( 1 − 1 p ) \phi(n)=n\prod_{p|n}(1-\frac{1}{p}) ϕ(n)=n∏p∣n(1−p1)
定理:
∑ d ∣ n ϕ ( d ) = n \sum_{d|n}\phi(d)=n ∑d∣nϕ(d)=n
g c d ( a , m ) = 1 ⇒ a ϕ ( m ) ≡ 1 m o d m gcd(a,m)=1\Rightarrow a^{\phi(m)}\equiv 1\ mod \ m gcd(a,m)=1⇒aϕ(m)≡1 mod m
前提条件是a,m互质
费马小定理
p是质数,a是整数,则 a p ≡ a m o d p a^p\equiv a\ mod\ p ap≡a mod p
威尔逊定理
p是素数, ( p − 1 ) ! ≡ − 1 m o d p (p-1)!\equiv -1\ mod \ p (p−1)!≡−1 mod p
逆元
定义: g c d ( a , m ) = 1 , ∃ gcd(a,m)=1,\exist gcd(a,m)=1,∃ b m o d m b\ mod \ m b mod m使得 a b ≡ 1 m o d m ab\equiv 1\ mod\ m ab≡1 mod m,称b是a的逆元
a,m必须互质,a才有逆元,逆元唯一
求逆:欧几里得扩展算法
gcd(a,n)=1时,求 a − 1 m o d n a^{-1}mod\ n a−1mod n
先用辗转相除法,拆到最后剩余1时回溯
线性同余方程组 ( a x = b m o d m ) (ax=b\ mod\ m) (ax=b mod m)
有解判定:令g=gcd(a,m),当且仅当g|b时,ax=b mod m才有解,且有g mod m个解
求线性同余方程组:中国剩余定理
{ x = a 1 m o d m 1 x = a 2 m o d m 2 . . . x = a k m o d m k \left\{\begin{matrix}x=a_1\ mod\ m_1 \\x=a_2\ mod\ m_2 \\... \\x=a_k\ mod\ m_k \end{matrix}\right. ⎩ ⎨ ⎧x=a1 mod m1x=a2 mod m2...x=ak mod mk
M i = ∏ m i m i M_i=\frac{\prod m_i}{m_i} Mi=mi∏mi
y i = M i − 1 m o d m i y_i=M_i^{-1}mod\ m_i yi=Mi−1mod mi
x = ∑ a i M i y i m o d ( ∏ m i ) x=\sum a_iM_iy_i\ mod (\prod m_i) x=∑aiMiyi mod(∏mi)
如果x前面有系数,先求逆乘到右边,将之化为标准形式
高次同余方程组
Hensel引理
f ( x ) ∈ Z ( x ) , f ( a ) = 0 m o d p k , f ′ ( a ) ≠ 0 m o d p ⇒ ∃ t m o d p , f ( a + t p k ) = 0 m o d p k + 1 f(x)\in Z(x),f(a)=0\ mod \ p^k,f'(a)\ne 0\ mod\ p\Rightarrow \exist t\ mod\ p,f(a+tp^k)=0\ mod\ p^{k+1} f(x)∈Z(x),f(a)=0 mod pk,f′(a)=0 mod p⇒∃t mod p,f(a+tpk)=0 mod pk+1
t唯一,且 t = − ( f ( a ) p k 1 f ′ ( a ) ) m o d p t=-(\frac{f(a)}{p^k}\frac{1}{f'(a)})mod\ p t=−(pkf(a)f′(a)1)mod p
代入t得 f ( a + t p k ) = f ( a − f ( a ) f ′ ( a ) ) f(a+tp^k)=f(a-\frac{f(a)}{f'(a)}) f(a+tpk)=f(a−f′(a)f(a))
模多项式
p是素数,f(x)最高次为n,f(x)=0 mod p最多有n个解
定理:
f ( x ) = x n + a n − 1 x n − 1 + . . . + a 0 f(x)=x^n+a_{n-1}x^{n-1}+...+a_0 f(x)=xn+an−1xn−1+...+a0,f(x)=0 mod p有n个不同解 ⇔ f ( x ) ∣ x p − x m o d p \Leftrightarrow f(x)|x^p-x\ mod\ p ⇔f(x)∣xp−x mod p
推论:
d ∣ p − 1 ⇒ x d = 1 m o d p d|p-1\Rightarrow x^d=1\ mod\ p d∣p−1⇒xd=1 mod p有d mod p个不同解
阶
定义:gcd(a,m)=1,满足 a h = 1 m o d m a^h=1\ mod\ m ah=1 mod m的最小正整数h是a mod m 的阶,写作 h = o r d m ( a ) h=ord_m(a) h=ordm(a)
定理:
- 其余满足该式的幂次都是h的倍数
- a k m o d m a^k\ mod\ m ak mod m的阶是 h g c d ( k , h ) \frac{h}{gcd(k,h)} gcd(k,h)h
- a mod m的阶是h,b mod m的阶是k,hk互素,则ab mod m的阶是hk
原根
定义:a mod m的阶是 ϕ ( m ) \phi(m) ϕ(m),则a是原根
定理:
p,q是素数, q e ∣ p − 1 q^e|p-1 qe∣p−1,则存在元素mod p的阶是 q e q^e qe
原根数量
mod m的原根数量是 ϕ ( ϕ ( m ) ) \phi(\phi(m)) ϕ(ϕ(m))
原根存在判定
当且仅当 m = 1 , 2 , 4 , p e , 2 p e m=1,2,4,p^e,2p^e m=1,2,4,pe,2pe时,m存在原根
平方剩余
定义:p是奇素数, a ≠ 0 m o d p a\ne 0\ mod\ p a=0 mod p,当 a = b 2 m o d p a=b^2\ mod\ p a=b2 mod p时,a是平方剩余,否则是平方非剩余
遇到一元二次方程,先化为上述标准形式
定理:
- a ≠ 0 m o d p , a p − 1 2 = 1 m o d p ⇒ a\ne 0\ mod\ p,a^{\frac{p-1}{2}}=1\ mod\ p\Rightarrow a=0 mod p,a2p−1=1 mod p⇒a是平方剩余
- 剩余集的一半数字是平方剩余,一半是非平方剩余
勒让德符号
写作 ( a p ) (\frac{a}{p}) (pa),=1表示a是mod p的平方剩余,=-1表示a是mod p的平方非剩余,=0表示a|p
定理:
- ( a p ) ( b p ) = ( a b p ) (\frac{a}{p})(\frac{b}{p})=(\frac{ab}{p}) (pa)(pb)=(pab)
高斯引理
- p是奇素数,a!=0,令 x p x_p xp为x mod p的平方剩余集中绝对值最小的数
n是
( a ) p , ( 2 a ) p , ( 3 a ) p , . . . , ( p − 1 2 a ) p (a)_p,(2a)_p,(3a)_p,...,(\frac{p-1}{2}a)_p (a)p,(2a)p,(3a)p,...,(2p−1a)p
中负数的个数,则 ( a p ) = ( − 1 ) n (\frac{a}{p})=(-1)^n (pa)=(−1)n - p是奇素数,gcd(a,p)=1,a是奇数
( a p ) = ( − 1 ) t (\frac{a}{p})=(-1)^t (pa)=(−1)t,其中 t = ∑ j = 1 p − 1 2 ⌊ j a p ⌋ t=\sum_{j=1}^{\frac{p-1}{2}} \left \lfloor \frac{ja}{p} \right \rfloor t=j=1∑2p−1⌊pja⌋ - ( a p ) = ( − 1 ) p 2 − 1 8 (\frac{a}{p})=(-1)^{\frac{p^2-1}{8}} (pa)=(−1)8p2−1
二次互反律 Quadratic Reciprocity Law
雅可比符号
Tonelli-Shanks算法(不考)
分圆多项式 Cyclotomic Polynomials
定义:对正整数n来说,能整除 x n − 1 x^n-1 xn−1但不能整除 x k − 1 ( k < n ) x^k-1(k
ϕ n ( x ) = ∏ 1 ≤ k ≤ n , g c d ( k , n ) = 1 x − e 2 i π k n \phi_n(x)=\prod_{1\le k\le n,gcd(k,n)=1}x-e^{2i\pi \frac{k}{n}} ϕn(x)=∏1≤k≤n,gcd(k,n)=1x−e2iπnk
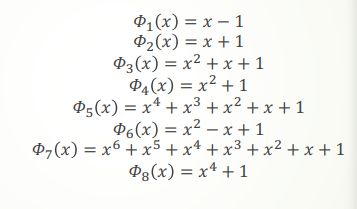
定理
- x n − 1 = ∏ d ∣ n ϕ d ( x ) x^n-1=\prod_{d|n}\phi_d(x) xn−1=∏d∣nϕd(x)
- ϕ n ( x ) \phi_n(x) ϕn(x)的最高次 n = ϕ ( x ) n=\phi(x) n=ϕ(x)
- 分圆多项式系数均为整数
- n>=2时,分圆多项式对称
- (不考)
- (不考)n是正整数,有无限个素数=1 mod n
算数函数 arithmetic function N->C
性质:
- 加性 f(mn)=f(m)+f(n)
- 乘性 f(mn)=f(m)f(n)
- 不完全 mn互质
- 完全 mn不互质
例子:
- v p i ( n ) v_{p_i}(n) vpi(n)是整除n的素数pi的最高次
- ω ( n ) \omega(n) ω(n)是n能分解出的素数的种类数
- Ω ( n ) \Omega(n) Ω(n)是n分解出的素数的幂次之和
- σ k ( n ) \sigma_k(n) σk(n)是n的正因数的k次方之和,k是复数
- k=0时,得到的是n的因子个数,记作d(n)
- k=1时,得到n的因数之和,记作 σ ( n ) \sigma(n) σ(n)
- 莫比乌斯函数
μ ( n ) = { ( − 1 ) ω ( n ) = ( − 1 ) Ω ( n ) , i f ω ( n ) = Ω ( n ) 0 , i f ω ( n ) ≠ Ω ( n ) \mu(n)=\begin{cases}(-1)^{\omega (n)}=(-1)^{\Omega (n)}, \ \ \ if\ \omega (n)=\Omega (n) \\0,\ \ \ if\ \omega (n)\ne \Omega (n) \end{cases} μ(n)={(−1)ω(n)=(−1)Ω(n), if ω(n)=Ω(n)0, if ω(n)=Ω(n) - f ( n ) = { 1 , i f n = 1 0 , i f o t h e r w i s e f(n)=\begin{cases}1, \ \ \ if\ n=1 \\0,\ \ \ if\ otherwise \end{cases} f(n)={1, if n=10, if otherwise
- π ( n ) \pi(n) π(n)是不超过n的素数个数
- 完美数是 σ ( n ) = 2 n \sigma(n)=2n σ(n)=2n的数,即因子之和=自身两倍的数,有6,28,496……
卷积(不考)
连分式 continued fraction
a 0 + 1 a 1 + 1 a 2 + 1 . . . + 1 a n a_0+\frac{1}{a_1+\frac{1}{a_2+\frac{1}{...+\frac{1}{a_n}}}} a0+a1+a2+...+an1111
简记作 [ a 0 , a 1 , . . . , a n ] [a_0,a_1,...,a_n] [a0,a1,...,an]
分数->连分式 使用辗转相除法
例子:
- 黄金分割率 ϕ : [ 1 , 1 , 1 , . . . ] \phi:[1,1,1,...] ϕ:[1,1,1,...]
- 2 : [ 1 , 2 , 2 , 2 , . . . ] \sqrt2:[1,2,2,2,...] 2:[1,2,2,2,...]
- π = [ 3 , 7 , 15 , 1 , 292 , 1 , 1 , 1 , 2 , 1 , 3 , 1 , . . . ] \pi=[3,7,15,1,292,1,1,1,2,1,3,1,...] π=[3,7,15,1,292,1,1,1,2,1,3,1,...]
- e = [ 2 , 1 , 2 , 1 , 1 , 4 , 1 , 1 , 6... ] e=[2,1,2,1,1,4,1,1,6...] e=[2,1,2,1,1,4,1,1,6...]
- 丢番图方程?
- [ a 0 , a 1 , . . . , a n ] = p k q k [a_0,a_1,...,a_n]=\frac{p_k}{q_k} [a0,a1,...,an]=qkpk
- p k − 1 q k − q k − 1 p k = ( − 1 ) k p_{k-1}q_k-q_{k-1}p_k=(-1)^k pk−1qk−qk−1pk=(−1)k
基本计数原理
加法原理
乘法原理
数学归纳法
马悖论
鸽巢原理
这个很好,很巧妙,很需要脑洞
容斥原理
乱序问题Derangement
答案是 d n = n ! ∑ k = 0 n ( − 1 ) k k ! d_n=n!\sum_{k=0}^n\frac{(-1)^k}{k!} dn=n!∑k=0nk!(−1)k
生成函数
可以利用生成函数通过递推关系求出通项
普通生成函数
G ( a n , x ) = ∑ n = 0 ∞ a n x n G(a_n,x)=\sum_{n=0}^\infty a_nx^n G(an,x)=∑n=0∞anxn
斐波那契数列
F 1 + F 2 + . . . + F n = F n + 2 − 1 F_1+F_2+...+F_n=F_{n+2}-1 F1+F2+...+Fn=Fn+2−1
- F 1 + F 3 + . . . + F 2 n − 1 = F 2 n F_1+F_3+...+F_{2n-1}=F_{2n} F1+F3+...+F2n−1=F2n
- F 2 + F 4 + . . . + F 2 n = F 2 n + 1 − 1 F_2+F_4+...+F_{2n}=F_{2n+1}-1 F2+F4+...+F2n=F2n+1−1
- F 1 − F 2 + . . . + ( − 1 ) n + 1 F n = ( − 1 ) n + 1 F n − 1 + 1 F_1-F_2+...+(-1)^{n+1}F_{n}=(-1)^{n+1}F_{n-1}+1 F1−F2+...+(−1)n+1Fn=(−1)n+1Fn−1+1
- F 1 2 + F 2 2 + . . . + F n 2 = F n F n + 1 F_1^2+F_2^2+...+F_n^2=F_nF_{n+1} F12+F22+...+Fn2=FnFn+1
指数生成函数(不考)
排列与组合
排列permutation
0!=1
- 可重集合multiset: n ! a 1 ! a 2 ! . . . a k ! \frac{n!}{a_1!a_2!...a_k!} a1!a2!...ak!n!
- 字符串全排列种类数 n k n^k nk
- n元素集合的子集数 2 n 2^n 2n
- 定义 P ( n , k ) = n ! ( n − k ) ! P(n,k)=\frac{n!}{(n-k)!} P(n,k)=(n−k)!n!
组合 Combination
( n k ) = n ! ( n − k ) ! k ! \begin{pmatrix}n \\k \end{pmatrix}=\frac{n!}{(n-k)!k!} (nk)=(n−k)!k!n!
定理:
- ( n k ) = ( n n − k ) \begin{pmatrix}n \\k \end{pmatrix}=\begin{pmatrix}n \\n-k \end{pmatrix} (nk)=(nn−k)
( n 0 ) = ( n n ) \begin{pmatrix}n \\0 \end{pmatrix}=\begin{pmatrix}n \\n \end{pmatrix} (n0)=(nn) - n中取k个元素的多重集合 ( n + k − 1 k ) \begin{pmatrix}n+k-1 \\k \end{pmatrix} (n+k−1k)
二项式系数
( x + y ) n = ∑ k = 0 n ( n k ) x n − k y k (x+y)^n=\sum_{k=0}^n\begin{pmatrix}n \\k \end{pmatrix}x^{n-k}y^k (x+y)n=∑k=0n(nk)xn−kyk
定理:
- ∑ k = 0 n ( − 1 ) k ( n k ) = 0 \sum_{k=0}^n(-1)^k\begin{pmatrix}n \\k \end{pmatrix}=0 ∑k=0n(−1)k(nk)=0
- ∑ k = 0 n ( n k ) = 2 n \sum_{k=0}^n\begin{pmatrix}n \\k \end{pmatrix}=2^n ∑k=0n(nk)=2n
- 递推公式(杨辉三角) ( n k ) = ( n − 1 k − 1 ) + ( n − 1 k ) \begin{pmatrix}n \\k \end{pmatrix}=\begin{pmatrix}n-1 \\k-1 \end{pmatrix}+\begin{pmatrix}n-1 \\k \end{pmatrix} (nk)=(n−1k−1)+(n−1k)
- ∑ m = k n ( m k ) = ( n + 1 k + 1 ) \sum _{m=k}^n\begin{pmatrix}m \\k \end{pmatrix}=\begin{pmatrix}n+1 \\k+1 \end{pmatrix} ∑m=kn(mk)=(n+1k+1)
- ∑ k = 0 n k ( n k ) = n 2 n − 1 \sum _{k=0}^nk\begin{pmatrix}n \\k \end{pmatrix}=n2^{n-1} ∑k=0nk(nk)=n2n−1
- ∑ j = 0 k ( m j ) ( n − m k − j ) = ( n k ) \sum _{j=0}^k\begin{pmatrix}m \\j \end{pmatrix}\begin{pmatrix}n-m \\k-j \end{pmatrix} =\begin{pmatrix}n \\k \end{pmatrix} ∑j=0k(mj)(n−mk−j)=(nk)
- ( n k ) ≥ ( n k + 1 ) \begin{pmatrix}n \\k \end{pmatrix}\ge \begin{pmatrix}n \\k+1 \end{pmatrix} (nk)≥(nk+1)
当且仅当n=2k+1,等号成立
多项式系数
借助 ( n a 1 , . . . , a k ) = n ! a 1 ! a 2 ! . . . a k ! \begin{pmatrix}n \\a_1,...,a_k \end{pmatrix}=\frac{n!}{a_1!a_2!...a_k!} (na1,...,ak)=a1!a2!...ak!n!
组成 composition
分糖果 糖果相同,人不同
n糖分给k人
- 每人至少一块(strong) ( n − 1 k − 1 ) \begin{pmatrix}n-1 \\k-1 \end{pmatrix} (n−1k−1)
- 可以分零块(weak) ( n + k − 1 k − 1 ) \begin{pmatrix}n+k-1 \\k-1 \end{pmatrix} (n+k−1k−1)
正整数n有 2 n − 1 2^{n-1} 2n−1个不同划分
集合划分 糖果不同,筐子相同
斯特林第二类数S(n,k)
递推公式 S(n,k)=S(n-1,k-1)+kS(n-1,k)
类似杨辉三角但有个系数k
贝尔数
B n B_n Bn是所有斯特林第二类数的加和
递推公式 B n + 1 = ∑ i = 0 n ( n i ) B i B_{n+1}=\sum_{i=0}^n\begin{pmatrix}n \\i \end{pmatrix}B_i Bn+1=∑i=0n(ni)Bi
整数划分 糖果相同,筐子相同
p(n)
Ferrers diagram
定理:
- n最多分k块的种类数=n分块中的最大数字不超过k
- n分奇数块的种类数=n的自共轭划分数
- 整数划分比集合划分种类少
卡特兰数
例子:
- 平衡括号
- 不超过对角线走格子
- 三角化
递推公式:
C n + 1 = ∑ i = 0 n C i C n − i , n ≥ 0 C_{n+1}=\sum_{i=0}^nC_iC_{n-i},n\ge 0 Cn+1=∑i=0nCiCn−i,n≥0
C0=1,C1=1
通项公式: C n = 1 n + 1 ( 2 n n ) C_n=\frac{1}{n+1}\begin{pmatrix}2n \\n \end{pmatrix} Cn=n+11(2nn)
数列:1,2,5,14,42,132……