人工蜂群算法(Artificial Bee Colony (ABC) Algorithm,附简单案例及详细matlab源码)
![]()
作者:非妃是公主
专栏:《智能优化算法》
博客地址:https://blog.csdn.net/myf_666
个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩
文章目录
- 专栏推荐
- 一、人工蜂群算法
- 二、伪代码
- 三、算法流程图
- 1. 初始化种群
- 2. 雇佣阶段
- 3. 观察阶段(跳舞来共享信息)
- 4. 侦察阶段
- 5. 算法终止条件
- 四、仿真实例
- 1. 问题
- 2. 分析
- 3. matlab代码实现
- 4. 效果展示
- the end……
专栏推荐
| 专栏名称 | 专栏地址 |
|---|---|
| 软件工程 | 专栏——软件工程 |
| 计算机图形学 | 专栏——计算机图形学 |
| 操作系统 | 专栏——操作系统 |
| 软件测试 | 专栏——软件测试 |
| 机器学习 | 专栏——机器学习 |
| 数据库 | 专栏——数据库 |
| 算法 | 专栏——算法 |
一、人工蜂群算法
人工蜂群(ABC)算法是一种基于蜂群的元启发式算法,由Karaboga在2005年提出(Karaboga, 2005),用于优化数值问题。它的灵感来自于蜜蜂的智能觅食行为。该算法特别基于Tereshko和Loengarov(2005)为蜜蜂群的觅食行为提出的模型。该模型由三个基本部分组成:就业和失业的觅食蜜蜂以及食物来源。前两个组成部分,即受雇和失业的觅食蜂,在其蜂巢附近寻找丰富的食物来源,这是第三个组成部分。该模型还定义了自我组织和集体智慧所必需的两种主要行为模式:将觅食者招募到丰富的食物来源,从而产生正反馈;觅食者放弃贫乏的食物来源,从而产生负反馈。
在ABC中,一个人工觅食蜂群(代理)搜索丰富的人工食物来源(对一个给定问题的良好解决方案)。为了应用ABC,所考虑的优化问题首先被转换为寻找使目标函数最小化的最佳参数向量的问题。然后,人工蜜蜂随机发现一个初始解决方案向量群,然后通过采用以下策略对其进行迭代改进:通过邻居搜索机制向更好的解决方案移动,同时放弃差的解决方案。
在ABC中,人工蜜蜂的蜂群包含三组蜜蜂:与特定食物来源相关的受雇蜜蜂,在蜂巢内观看雇佣蜜蜂的舞蹈以选择食物来源的观察蜜蜂,以及随机搜索食物来源的侦察蜜蜂。观察者和侦察者也都被称为无业蜜蜂。最初,所有的食物源位置都由侦察蜂发现。此后,食物源的花蜜被就业蜂和围观蜂开发,这种持续的开发最终会使它们变得枯竭。然后,正在开发已耗尽的食物来源的受雇蜂就会变成侦察蜂,再次寻找更多的食物来源。换句话说,食物来源已被耗尽的受雇蜂成为侦察蜂。在ABC中,食物源的位置代表问题的可能解决方案,食物源的花蜜量对应于相关解决方案的质量(适应度)。受雇蜜蜂的数量等于食物源(解决方案)的数量,因为每只受雇蜜蜂都与一个且仅有一个食物源相关。1
二、伪代码
伪代码如下:
Initialization Phase
REPEAT
Employed Bees Phase
Onlooker Bees Phase
Scout Bees Phase
Memorize the best solution achieved so far
UNTIL(Cycle=Maximum Cycle Number or a Maximum CPU time)
三、算法流程图
人工蜂群的算法流程图如下:
1. 初始化种群
x m i = l i + r a n d ( 0 , 1 ) × ( u i − l i ) x_{mi}=l_i+rand(0,1)\times (u_i-l_i) xmi=li+rand(0,1)×(ui−li)
2. 雇佣阶段
通过如下公式产生新个体:
v m i = x m i + ϕ m i ( x m i − x k i ) v_{mi}=x_{mi}+\phi_{mi}(x_{mi}-x_{ki}) vmi=xmi+ϕmi(xmi−xki)
产生个体的同时,根据新种群和老种群进行贪婪选择,留下好的个体,这样就形成了新的个体。
然后,通过如下公式计算个体的适应度(与函数值反相关):
f i t m ( x m ⃗ ) = { 1 1 + f m ( x m ⃗ ) i f f m ( x m ⃗ ) ≥ 0 1 + a b s ( f m ( x m ⃗ ) ) i f f m ( x m ⃗ ) < 0 fit_m(\vec{x_m})= \left\{ \begin{matrix} \frac{1}{1+f_m(\vec{x_m})} & if & f_m(\vec{x_m})\geq0\\ 1+abs(f_m(\vec{x_m})) & if &f_m(\vec{x_m})<0 \\ \end{matrix} \right. fitm(xm)={1+fm(xm)11+abs(fm(xm))ififfm(xm)≥0fm(xm)<0
3. 观察阶段(跳舞来共享信息)
p m = f i t m ( x m ⃗ ) ∑ m = 1 S N f i t m ( x m ⃗ ) p_m=\frac{fit_m(\vec{x_m})}{\sum_{m=1}^{SN} fit_m(\vec{x_m})} pm=∑m=1SNfitm(xm)fitm(xm)
4. 侦察阶段
如果,在一定次数内,一个雇佣蜂没有被围观蜂的围观而得到提高,那么到达这个次数后就被解雇了,重新初始化,这被称为侦察,初始化方法和最初一样,如下:
x i = l i + r a n d ( 0 , 1 ) × ( u i − l i ) x_{i}=l_i+rand(0,1)\times (u_i-l_i) xi=li+rand(0,1)×(ui−li)
5. 算法终止条件
算法迭代运行MaxCycles后,跳出循环终止运行。
四、仿真实例
1. 问题
求解下面函数的最小值:
f ( x ) = ∑ i = 1 9 100 × ( x i + 1 − x i 2 ) 2 + ( 1 − x i ) 2 f(x)=\sum_{i=1}^{9}100\times(x_{i+1}-x_i^2)^2+(1-x_i)^2 f(x)=i=1∑9100×(xi+1−xi2)2+(1−xi)2
其中, − 10 ≤ x i ≤ 10 -10\leq x_i\leq 10 −10≤xi≤10.
全局最优解为: x i = 1 ; f m i n = 0 x_i=1 ; fmin=0 xi=1;fmin=0.
2. 分析
这是一个连续的实数函数优化问题,一共有10个变量,因此我们的种群个体要有10个维度,同时设置合理的种群数量,然后即可利用进行人工蜂群算法进行优化。
3. matlab代码实现
下面的代码2源于人工蚁群算法(Artificial Bee Colony (ABC) Algorithm)的官网:https://abc.erciyes.edu.tr/.
本人根据matlab最新版本进行了简要修改,具体思路并不便于描述,但已经进行了逐行注释,感兴趣的朋友可以阅读一下。
%%%%%ARTIFICIAL BEE COLONY ALGORITHM%%%%
%Artificial Bee Colony Algorithm was developed by Dervis Karaboga in 2005
%by simulating the foraging behaviour of bees.
%Copyright @2008 Erciyes University, Intelligent Systems Research Group, The Dept. of Computer Engineering
%Contact:
%Dervis Karaboga ([email protected] )
%Bahriye Basturk Akay ([email protected])
clear all
close all
clc
% 设置 ABC 算法控制参数
% 三连点(省略号)...表示续行。
% 当一行内语句太长,可以使用三个点...表示续行,另起一行。
ABCOpts = struct( 'ColonySize', 10, ... % 雇佣蜂数量+ 观察蜂数量
'MaxCycles', 2000,... % 终止算法的最大周期数
'ErrGoal', 1e-20, ... % 错误目标,以便终止算法(在当前版本的代码中没有使用)。
'Dim', 10 , ... % 目标函数的参数维度 dimention
'Limit', 100, ... % 控制参数,以便放弃食物来源
'lb', -3, ... % 待优化参数的下限
'ub', 3, ... % 待优化参数的上限
'ObjFun' , 'rosenbrock', ... % 写出你想最小化的目标函数的名称
'RunTime',3); % 运行的次数
GlobalMins=zeros(ABCOpts.RunTime,ABCOpts.MaxCycles);% 运行次数以及终止最大周期数
for r=1:ABCOpts.RunTime % 外层循环——运行次数
% 初始化种群
Range = repmat((ABCOpts.ub-ABCOpts.lb),[ABCOpts.ColonySize ABCOpts.Dim]); % 初始化每一维度的范围
Lower = repmat(ABCOpts.lb, [ABCOpts.ColonySize ABCOpts.Dim]); % 初始化每一维度的下限
Colony = rand(ABCOpts.ColonySize,ABCOpts.Dim) .* Range + Lower; % 在每一维度的范围内,随机初始化种群
Employed=Colony(1:(ABCOpts.ColonySize/2),:); % 前一半个体为雇佣蜂
% 评估和计算适应度
ObjEmp=feval(ABCOpts.ObjFun,Employed); % 计算函数值
FitEmp=calculateFitness(ObjEmp); % 计算适应度
% 设置雇佣蜂Bas的初始值为0,表示没有改进的次数为0
Bas=zeros(1,(ABCOpts.ColonySize/2));
GlobalMin=ObjEmp(find(ObjEmp==min(ObjEmp),end)); % 雇佣蜂中的最优函数值
GlobalParams=Employed(find(ObjEmp==min(ObjEmp),end),:); % 雇佣蜂中的最优解
Cycle=1; % 从 1 开始
while ((Cycle <= ABCOpts.MaxCycles)) % 开始进行迭代
%%%%% 雇佣阶段
Employed2=Employed; % 新一代雇佣蜂
for i=1:ABCOpts.ColonySize/2 % 遍历雇佣蜂个体
Param2Change=fix(rand*ABCOpts.Dim)+1; % 选择更改的维度
neighbour=fix(rand*(ABCOpts.ColonySize/2))+1; % 选择更改的蜜蜂
while(neighbour==i) % 保证需要更改的蜜蜂不和当前蜜蜂相同
neighbour=fix(rand*(ABCOpts.ColonySize/2))+1;
end
% 产生新的群体
Employed2(i,Param2Change)=Employed(i,Param2Change)+(Employed(i,Param2Change)-Employed(neighbour,Param2Change))*(rand-0.5)*2;
% 限制范围
if (Employed2(i,Param2Change)<ABCOpts.lb)
Employed2(i,Param2Change)=ABCOpts.lb;
end
if (Employed2(i,Param2Change)>ABCOpts.ub)
Employed2(i,Param2Change)=ABCOpts.ub;
end
end
ObjEmp2=feval(ABCOpts.ObjFun,Employed2); % 重新评估
FitEmp2=calculateFitness(ObjEmp2); % 重新计算适应度
% 进行贪婪选择
[Employed, ObjEmp, FitEmp, Bas]=GreedySelection(Employed,Employed2,ObjEmp,ObjEmp2,FitEmp,FitEmp2,Bas,ABCOpts);
% 根据适应度正则化为概率
NormFit=FitEmp/sum(FitEmp);
%%% 观察阶段
Employed2=Employed; % 将新老种群同步
i=1;
t=0;
while(t<ABCOpts.ColonySize/2) % 进行观察
if(rand<NormFit(i)) % 进行轮盘赌
t=t+1; % 记忆轮盘赌的次数
Param2Change=fix(rand*ABCOpts.Dim)+1; % 获取观察选择的维度
neighbour=fix(rand*(ABCOpts.ColonySize/2))+1; % 选择一个被观察的个体
while(neighbour==i) % 被观察个体不能与当前个体相同
neighbour=fix(rand*(ABCOpts.ColonySize/2))+1;
end
Employed2(i,:)=Employed(i,:); % 由于上次的被观察,可能导致观察蜂和雇佣蜂不一致
% 进行观察
Employed2(i,Param2Change)=Employed(i,Param2Change)+(Employed(i,Param2Change)-Employed(neighbour,Param2Change))*(rand-0.5)*2;
if (Employed2(i,Param2Change)<ABCOpts.lb) % 如果超出下限
Employed2(i,Param2Change)=ABCOpts.lb; % 置为下限
end
if (Employed2(i,Param2Change)>ABCOpts.ub) % 如果超出上限
Employed2(i,Param2Change)=ABCOpts.ub; % 置为上限
end
ObjEmp2=feval(ABCOpts.ObjFun,Employed2); % 计算目标函数值
FitEmp2=calculateFitness(ObjEmp2); % 计算适应度
% 进行贪心选择
[Employed, ObjEmp, FitEmp, Bas]=GreedySelection(Employed,Employed2,ObjEmp,ObjEmp2,FitEmp,FitEmp2,Bas,ABCOpts,i);
end
i=i+1; % i+1,下一个个体被观察
if (i==(ABCOpts.ColonySize/2)+1) % 如果 i 超出索引
i=1; % 重新置为 1
end
end
%%% 记录最优个体
CycleBestIndex=find(FitEmp==max(FitEmp)); % 寻找最优个体,可能是多个
CycleBestIndex=CycleBestIndex(end); % 选择最后一个,变为1个
CycleBestParams=Employed(CycleBestIndex,:); % 记录它的参数
CycleMin=ObjEmp(CycleBestIndex); % 记录目标函数值
if CycleMin<GlobalMin % 记录全局最优个体,防止最优个体丢失
GlobalMin=CycleMin;
GlobalParams=CycleBestParams;
end
GlobalMins(r,Cycle)=GlobalMin; % 追踪每一次循环的最优个体
%% 侦察阶段
ind=find(Bas==max(Bas)); % 查找没有变优次数最多的个体
ind=ind(end); % 可能有很多个,选择最后一个
if (Bas(ind)>ABCOpts.Limit) % 判断是否大于限制
Bas(ind)=0; % 重新开始计数
Employed(ind,:)=(ABCOpts.ub-ABCOpts.lb)*(0.5-rand(1,ABCOpts.Dim))*2;% 进行侦察操作
%message=strcat('burada',num2str(ind))
end
ObjEmp=feval(ABCOpts.ObjFun,Employed); % 重新评估种群
FitEmp=calculateFitness(ObjEmp); % 计算适应值函数
fprintf('Cycle=%d ObjVal=%g\n',Cycle,GlobalMin); % 打印每个cycle的最优个体
Cycle=Cycle+1;
end % End of ABC
end %end of runs
semilogy(mean(GlobalMins))
title('Mean of Best function values');
xlabel('cycles');
ylabel('error');
fprintf('Mean =%g Std=%g\n',mean(GlobalMins(:,end)),std(GlobalMins(:,end)));
calculateFitness.m函数如下:
function fFitness=calculateFitness(fObjV)
fFitness=zeros(size(fObjV));
ind=find(fObjV>=0);
fFitness(ind)=1./(fObjV(ind)+1);
ind=find(fObjV<0);
fFitness(ind)=1+abs(fObjV(ind));
rosenbrok.m 函数定义如下:
function ObjVal = rosenbrock(Chrom,~)
% Dimension of objective function
Dim=size(Chrom,2); % 获取第 2 维的长度
% Compute population parameters
[~,Nvar] = size(Chrom);
% function 11, sum of 100* (x(i+1) -xi^2)^2+(1-xi)^2 for i = 1:Dim (Dim=10)
% n = Dim, -10 <= xi <= 10
% global minimum at (xi)=(1) ; fmin=0
Mat1 = Chrom(:,1:Nvar-1);
Mat2 = Chrom(:,2:Nvar);
if Dim == 2
ObjVal = 100*(Mat2-Mat1.^2).^2+(1-Mat1).^2;
else
ObjVal =transpose(sum(transpose((100*(Mat2-Mat1.^2).^2+(1-Mat1).^2)))); % 注意这里用了两个转置
end
% End of function
GreedySelection.m 函数定义如下:
function [Colony, Obj, Fit, oBas]=GreedySelection(Colony1,Colony2,ObjEmp,ObjEmp2,FitEmp,FitEmp2,fbas,ABCOpts,i)
oBas=fbas;
Obj=ObjEmp;
Fit=FitEmp;
Colony=Colony1;
if (nargin==8)
for ind=1:size(Colony1,1)
if (FitEmp2(ind)>FitEmp(ind))
oBas(ind)=0;
Fit(ind)=FitEmp2(ind);
Obj(ind)=ObjEmp2(ind);
Colony(ind,:)=Colony2(ind,:);
else
oBas(ind)=fbas(ind)+1;
Fit(ind)=FitEmp(ind);
Obj(ind)=ObjEmp(ind);
Colony(ind,:)=Colony1(ind,:);
end
end %for
end %if
if(nargin==9)
ind=i;
if (FitEmp2(ind)>FitEmp(ind))
oBas(ind)=0;
Fit(ind)=FitEmp2(ind);
Obj(ind)=ObjEmp2(ind);
Colony(ind,:)=Colony2(ind,:);
else
oBas(ind)=fbas(ind)+1;
Fit(ind)=FitEmp(ind);
Obj(ind)=ObjEmp(ind);
Colony(ind,:)=Colony1(ind,:);
end
end
4. 效果展示
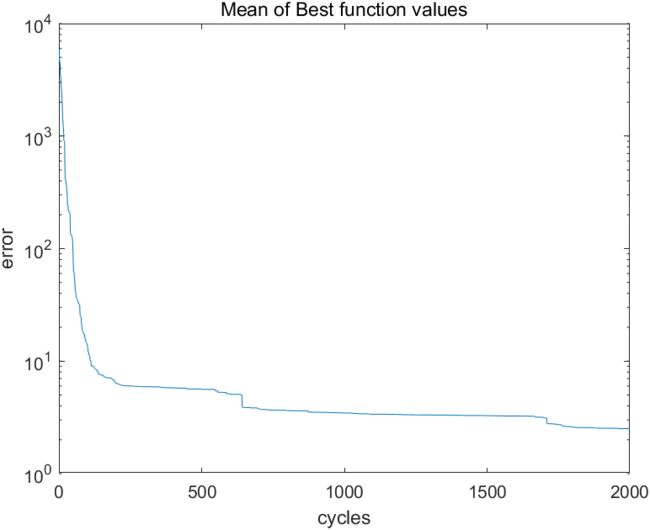
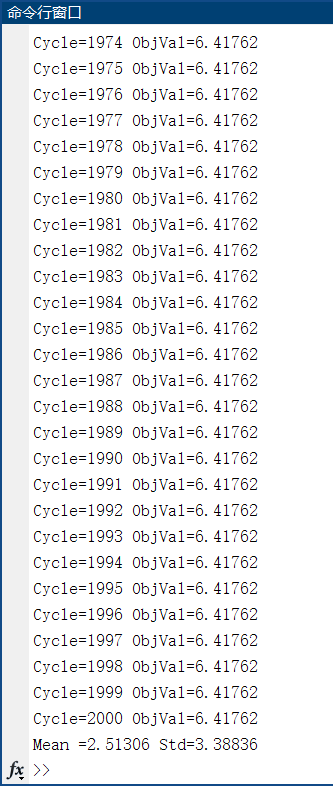
多次运行上述代码,最终寻得的最优解,以及适应度曲线分别如下:
第一次运行如下:
第三次运行:
第四次运行:
第五次运行:
可以看到对于求解 rosenbroke 的最小值问题,人工蜂群(Artificial Bee Colony)算法每次运行的结果都有很大的差别,证明人工蜂群(Artificial Bee Colony)算法在收敛性上还是存在一定问题的。
the end……
人工蜂群算法到这里就要结束啦~~到此既是缘分,欢迎您的点赞、评论、收藏!关注我,不迷路,我们下期再见!!
我是Cherries,一位计算机科班在校大学生,写博客用来记录自己平时的所思所想!
内容繁杂,又才疏学浅,难免存在错误,欢迎各位大佬的批评指正!
我们相互交流,共同进步!
注:本文由
非妃是公主发布于https://blog.csdn.net/myf_666,转载请务必标明原文链接:https://blog.csdn.net/myf_666/article/details/129363425
Dervis Karaboga (2010) Artificial bee colony algorithm. Scholarpedia, 5(3):6915. ↩︎
https://abc.erciyes.edu.tr/ ↩︎