ResNet 论文理解含视频
-
- ResNet 论文理解
-
- 问题导引论文理解
-
- Q1.神经网络真的越深越好吗?
- Q2. 为什么加深网络会带来退化问题?
- Q3. 如何构建更深层的网络?
- 基于残差的深度学习框架
-
- Residual Learning 的理论依据
- 网络结构
- ResNet 的成绩
- 总结
- 视频理解
-
- 引入
- 恒等映射
ResNet 论文理解
问题导引论文理解
ResNet 网络的论文名字是《Deep Residual Learning for Image Recognition》,发表在2016年的 CVPR 上,获得了 最佳论文奖。ResNet 中的 Res 也是 Residual 的缩写,它的用意在于基于 残差 学习,让神经网络能够越来越深,准确率越来越高。
深度残差网络(deep residual network)是该论文中提出的一种全新的网络结构,其核心模块是 残差块 residual block。正是由于残差块结构的出现使得深度神经网络模型的层数可以不断加深到100层、1000层甚至更深。
自 2012 年 AlexNet 在 ILSVRC 一战成名后,卷积神经网络便一发不可收拾,后续的各类竞赛中各种神经网络都大发异彩,除了更高的准确率之外,它们普遍的特征就是,网络的层级越来越深 了。
ILSVRC是ImageNet Large Scale Visual Recognition Challenge的缩写,是一个从2010年开始举办的 大规模图像识别竞赛,使用ImageNet数据集的一个子集,总共有1000类。
ILSVRC的目的是评估算法在对象检测和图像分类方面的性能,同时也推动了计算机视觉领域的发展。ILSVRC每年都有一个相应的研讨会,在其中展示竞赛的方法和结果。
ILSVRC的获奖网络是指在 图像分类任务中取得最佳成绩的卷积神经网络(CNN)。从2012年开始,ILSVRC的冠军网络都是基于CNN的深度学习模型,它们在提高图像识别的准确率和效率方面都有重要的贡献。以下是
ILSVRC历届冠军网络的简介:
- 2012年:AlexNet,由 Alex Krizhevsky 等人提出,使用了 8层 CNN 和 ReLU 激活函数,利用GPU加速训练,首次在 ILSVRC 上 大幅度降低了错误率,引发了深度学习的热潮。
- 2013年:ZFNet,由 Matthew Zeiler 和 Rob Fergus 提出,对AlexNet进行了一些改进,主要是调整了第一层卷积核的大小和步长,以及使用了 可视化 方法来分析网络的特征。
- 2014年:VGGNet,由牛津大学的 Karen Simonyan 和 Andrew Zisserman 提出,使用了 16层或19层 CNN,统一了卷积核的大小为3x3,展示了 网络深度对性能的影响。
- 2014年:GoogLeNet,由Google的 Christian Szegedy 等人提出,使用了22层CNN,引入了 Inception 模块,可以有效地增加网络宽度和深度,同时减少参数和计算量。
- 2015年:ResNet,由微软亚洲研究院的何恺明等人提出,使用了 152层CNN,引入了 残差连接(Residual Connection),可以 有效地解决深度网络的退化问题,刷新了图像识别的记录。
- 2016年:Inception-v4/Inception-ResNet-v2,由Google的Christian Szegedy等人提出,结合了 Inception 模块和残差连接,进一步提高了网络性能。
- 2017年:SENet(Squeeze-and-Excitation Network),由牛津大学的Jie Hu等人提出,引入了 SE 模块,可以 自适应地调整特征图的权重,增强了特征表达能力。
Inception 模块是一种图像模型的组成部分,旨在 近似一个最优的局部稀疏结构。简单地说,它 允许我们在一个图像块中使用多种类型的卷积核大小,而不是被限制在一个单一的卷积核大小,然后 将它们拼接起来传递到下一层。
- Inception模块的设计思想是 为了减少计算和参数的开销,同时 增加网络的宽度和深度,提高对不同尺度信息的适应性。
- Inception 模块有多个版本,如 Inception v1(GoogLeNet),Inception v2,Inception v3,Inception v4和 Inception-ResNet 等,它们都在不同的方面对Inception 模块进行了改进和优化。
Q1.神经网络真的越深越好吗?
深度学习的发展从 LeNet 到 AlexNet,再到 VGGNet 和 GoogLeNet,网络的深度在不断加深,经验表明,网络深度有着至关重要的影响,层数深的网络可以提取出图片的低层、中层和高层特征。
神经网络真的越深越好吗?
情况不是这样的,如果神经网络越来越深,这个神经网络可能会出现 退化(degradation) 的现象。即在深度神经网络中,如果不断增加网络的层数,可能会出现一个问题,就是 网络的训练精度和测试精度都不再提高,甚至开始下降。
当更深的网络能够开始收敛时,一个退化问题就暴露出来了:随着网络深度的增加,精度趋于饱和(这可能不足为奇),然后迅速退化。出乎意料的是,这种退化并 不是由过拟合引起 的,在 适当深度的模型上增加更多的层会导致更高的训练误差。
 在 CIFAR-10 这个小型的数据集上,56 层的神经网络的表现比不过 20 层的神经网络。
在 CIFAR-10 这个小型的数据集上,56 层的神经网络的表现比不过 20 层的神经网络。
Q2. 为什么加深网络会带来退化问题?
- 即使新增的这些 layer 什么都没学习,保持恒等输出(所有的 weight 都设为1),那么按理说网络的精度也应该 = 原有未加深时的水平;
- 如果新增的 layer 学习到了有用特征,那么必然加深过后的模型精度会 > 未加深的原网络。
看起来对于网络的精度加深后都应该 >= 加深前才对啊 ?
实际上,让新增的 layer 保持什么都不学习的恒等状态,恰恰很困难,因为在训练过程中 每一层 layer 都通过线性修正单元 relu 处理,而这样的处理方式会 带来特征的信息损失(不论是有效特征or冗余特征)。
所以上述假设的前提是不成立的,简单的堆叠 layer 可能会带来退化问题。
Q3. 如何构建更深层的网络?
到此,何凯明团队创新地提出了 残差块 的构想,通过 shortcut/skip connection 这样的方式(最初出现在 highway network中),绕过这些 普通的堆叠块,既然保持 堆叠块 的 identity 恒等性很困难,那就直接绕过它们,通过 shortcut 通路来保持恒等。 如下图:
同样的堆叠块网络,加上恒等映射 x x x 后,mapping 也随之改变。普通网络的 underlying mapping 是 H ( x ) \mathcal H(x) H(x),加上恒等映射 x x x 后,变成了残差 mapping 是 F ( x ) \mathcal F(x) F(x),那么之前的 H ( x ) \mathcal H(x) H(x) 被强制转换为 H ( x ) : = F ( x ) + x \mathcal H(x) := \mathcal F(x) + x H(x):=F(x)+x。
反向传播算法会自动找最优参数,当经过这些图左边 普通的堆叠块网络,如果 输出的效果比输入更差(那还不如不学习,想让网络输出仍然是 x x x),
- 考虑情况,不加图右边的恒等映射 x x x,就是原来的网络要拟合输入 x x x,这相当于是 让网络学习恒等映射,这是困难的(实验结果证明);
- 而加上恒等映射 x x x 后,只需要让网络推向0,这是更容易的(实验结果证明)。
这就保证了 深层网络起码不会越学习越差。
这种训练方式称为残差学习,这种结构块也称为 Residual Block 残差块。正是残差结构的出现,使得残差网络能很好的加深网络层数,同时解决退化问题。
基于残差的深度学习框架
论文中说:
有一个解决方案是:在一个的常规的比较浅的模型上添加新的层,而新的层是基于 identity mapping 恒等映射的。
就是在一个浅层的网络模型上进行改造,然后将新的模型与原来的浅层模型相比较,这里有个底线就是,改造后的模型至少不应该比原来的模型表现要差。因为 新加的层可以让它的结果为 0,这样它就等同于原来的模型了。 这个假设是 ResNet 的出发点。
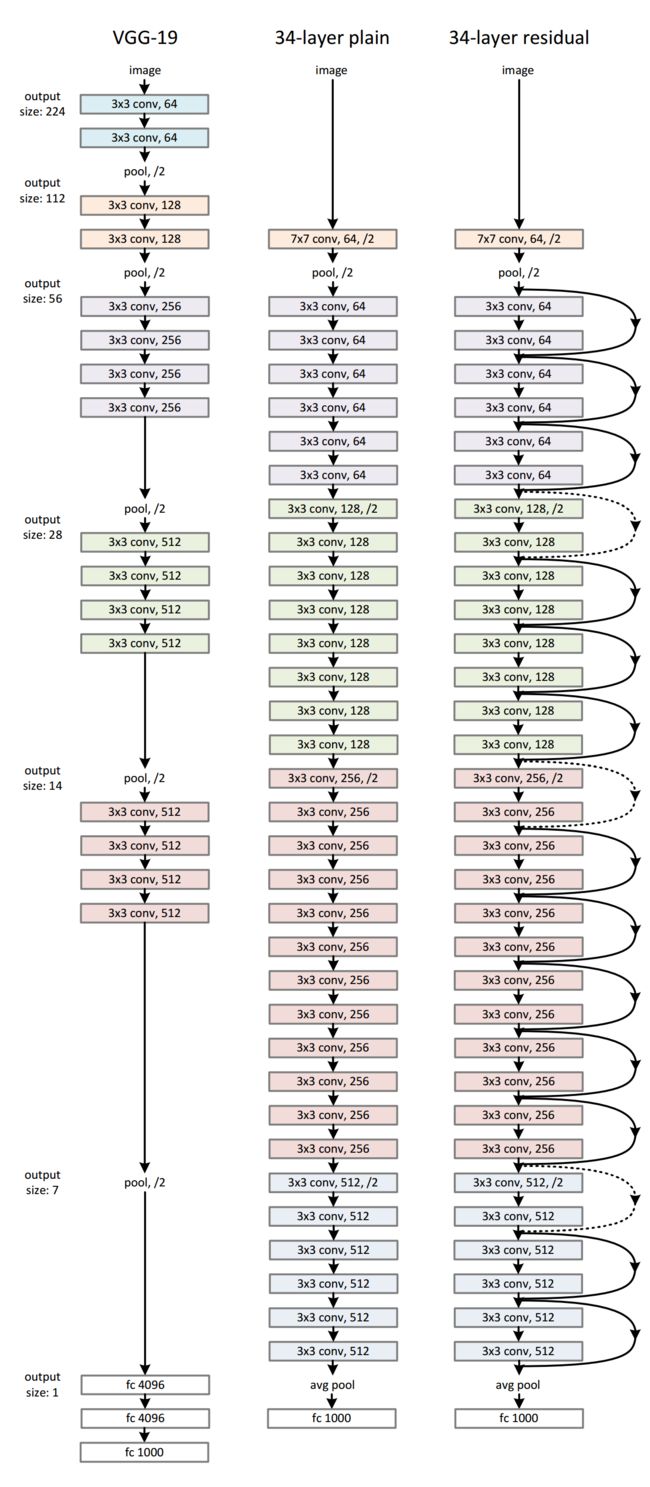
个人觉得,论文中的下图可以这样理解:
- 这个 比较浅的模型 就是大名鼎鼎的 VGG-19;
- 然后中间的是在 VGG-19 的模型上 添加新的层后形成的 34-layer 普通网络;
- 为了保证改造后的模型至少不比原来的模型表现差,加上恒等映射,即右边的 34-layer 残差网络。
从 34-layer plain 到 34-layer residual 不需要额外的参数。
作者引入了 deep residual learning framework,也就是 基于残差的深度学习框架,实际上是对常规的神经网络的改造。
目前流行的神经网络都可以看成是 卷积层的堆叠,可以用栈来表示,我们就叫它卷积栈好了。
输入数据经过每个卷积层都会发生变化,产生新的 feature map ,我们可以说 数据在输入与输出间发生了映射,也就是 mapping。神经网络中的权重参数 一个作用就是 去拟合这种输入与输出之间的 mapping。
ResNet 准备从这一块动手,假设现在有一个栈的卷积层比如说 2 个卷积层堆叠,将 当前这个栈的输入 与 后面的栈的输入(也就是当前这个栈的输出)之间的 mapping 称为 underlying mapping,现在的工作是企图替换它引入一种新的 mapping 关系,ResNet 称之为 residual mapping 去替换常规的 mapping 关系。
意思是与其让卷积栈直接拟合 underlying mapping,不如让它去拟合 residual mapping。而 residual mapping 和 underlying mapping 其实是有关联的。
- 将 underlying mapping 标记为 H ( x ) \mathcal H ( x ) H(x)
- 将经过堆叠的非线性层产生的 mapping 标记为 F ( x ) : = H ( x ) − x \mathcal F ( x ) : = \mathcal H ( x ) − x F(x):=H(x)−x
- 所以,最原始的 mapping 就被强制转换成 F ( x ) + x \mathcal F ( x ) + x F(x)+x
然后,作者假设对 residual mapping 的优化要比常规的 underlying mapping 要简单和容易。
而 F ( x ) + x \mathcal F ( x ) + x F(x)+x 在 实际的编码过程 中,可以被一种叫做 快捷连接 的结构件来实现。

快捷连接通常会跳过 1 个或者多个层,在 ResNet 中快捷连接直接运用了 identity mapping,意思就是 将一个卷积栈的输入直接与这个卷积栈的输出相加。
F ( x ) \mathcal F ( x ) F(x) 表示残差,最理想的情况是 identity mapping 是最优的输出,那么让 F ( x ) \mathcal F ( x ) F(x) 为 0 就好了,现实是 F ( x ) \mathcal F ( x ) F(x) 不可能全为 0,那么这些多出来的东西就可以增强网络的表达能力。
Residual Learning 的理论依据
我们可以将焦点放在 H ( x ) \mathcal H ( x ) H(x) 上。
理论上有一种假设,多层卷积的参数可以近似地估计很复杂的函数表达公式的值,那么多层卷积也肯定可以近似地估计 H ( x ) − x \mathcal H ( x ) − x H(x)−x 这种残差公式。
所以与其让卷积栈去近似的估计 H ( x ) \mathcal H(x) H(x),还不如让它去近似地估计 F ( x ) : = H ( x ) − x \mathcal F(x):=\mathcal H(x)-x F(x):=H(x)−x,而 F ( x ) \mathcal F(x) F(x) 就是残差。
作者假设的是,残差比原始的 mapping 更容易学习。
作者在他的另外一篇论文《Identity Mappings in Deep Residual Networks》中给出了详细的讨论。
网络结构
ResNet 的起始是从一个 常规的比较浅的网络上探求加层的过程。这个常规的比较浅的网络是大名鼎鼎的 VGG-19。
作者对 VGG-19 进行仿制与改造,得到了一个 34 层的 plain network,然后又在这个 34 层的 plain network 中插入快捷连接,最终形成了一个 34 层的 residual network。
F ( x ) \mathcal F(x) F(x) 要与 x x x 相加,那么它们的维度就需要一样。而 ResNet 采用的是 用 1x1 的卷积核去应对维度的变化,通过 1x1 的卷积核去 对输入进行升维和降维。
ResNet 作者做了大量的模型评估工作,网络的层数从 18 到 152 都有试验。
值得注意的是,从 50-layer 起,ResNet 采用了一种 bottleneck design 的手段。
1x1 的卷积核让整个残差单元变得更加细长,这也是 bottleneck 的含义,更重要的是 参数减少 了。
最终在 ImageNet 验证集上的表现也证明了 ResNet 比当时其他网络要强,并且 ResNet 本身层级越多准确率越高。
最后,为了证明 ResNet 的 泛化能力,作者也在 CIFAR-10 数据集上做了测试和分析,ResNet 甚至做到了 1000 层以上。这证明了 基于残差学习可以让网络更深。
ResNet 的成绩
ResNet 依靠成绩说话,
- 它是 ILSVRC 2015 年图像分类冠军。
而且 ResNet 的 泛化 变现也很卓越,在
- ImageNet 目标检测
- ImageNet 目标定位
- COCO 目标检测
- COCO 图像分割
等竞赛中 都取得了当年(2015)的冠军。
并且,ResNet 是:
- 当年 ImageNet 参赛模型中层级最深的模型,达到了 152层
这些证据证明了 ResNet 加深网络后,性能比其他的模型更突出。
总结
- 论文 更多讲述的是经验,这些经验 靠实验结果 表现出了 ResNet 的高效,但 后来的补充材料给出了理论依据,自此它才变得更加 让人信服。
- ResNet 是 基于浅层网络的探索性的结果,就如 VGG 是在 AlexNet 的基础上探索得到的。
- ResNet 验证了大量的结构,并且进行了 大量的横向和纵向对比 才得到的 最理想的结果。
参考:
【深度学习】经典神经网络 ResNet 论文解读
视频理解
下面的视频,用图形的方式解释了 ResNet 的原理和优势:https://www.youtube.com/watch?v=GWt6Fu05voI
现在,残差连接 无处不在,不仅仅是在图像识别中,它们也出现在变换器(Transformer)中,以及你能想到的任何地方,你很可能会在某个地方找到一些残差连接。
变换器是一种基于自注意力机制(self-attention)的神经网络模型,用于 处理序列数据,如自然语言处理(NLP)和语音识别(ASR)等领域。
- 变换器的优点是 可以捕捉序列中任意位置之间的依赖关系,而不受距离的限制,同时也可以实现高效的并行计算。
- 从 Transformer 推出至今,已经成为众多模型的核心模块,比如大家熟悉的 BERT、T5 等都有 Transformer 的身影,就连近段时间爆火的 ChatGPT 也依赖 Transformer。
引入
将一张图像输入到卷积层中,首先会保持较大的分辨率,但会增加通道数量,然后随着过滤器数量的增加,你会缩小图像的比例。这样你就会堆叠越来越多的过滤器,同时缩小图像的分辨率。如果你在进行图像分类,比如你想把它分类为乐高塔或其他任何东西,它在哪里并不那么重要。
在较低的层次上,你会想要 解析出像边缘等非常低层的特征,它们所在的地方是重要的。然后你往上走,去到越来越多的抽象特征,随着你往上走,这些神经网络 倾向于学习越来越多的抽象特征。
假设是这些抽象特征的精确定位会越来越不重要,所以如果你认识到有一个矩形,那么它在哪里并不重要,重要的是它在那里的某个地方,也许它与另一个矩形有关系。
所以如果想识别一辆汽车,
- 下层会识别有边缘的事实;
- 然后 中间层会识别出轮子和这些方的几何形状,但它们到底在哪里并不重要;
- 然后 更高层会学会将各个部分相互组合,这些东西在哪里变得越来越不重要。
越来越重要的是你建立更具表现力的特征,这样人们就会 降低分辨率,增加过滤器的数量,这是一个很好的启发式方法。
但这基本上就是这些网络的架构,我们会质疑为什么增加了层数,它会变得更糟。
恒等映射
理论上,存在一种解,增加层数应该不会变得更糟:
假如我有一个5层的网络,我想构建更深的9层网络,那么我拿来5层网络作为前5层,后4层网络只需要完成恒等映射的任务,
- 按理来说,就可以保证更深的9层网络不会比5层的网络效果差,
- 但 实验效果 却是9层网络效果更差,这说明后4层网络不太能完成恒等映射。
所以作者团队后面就 不用网络来拟合恒等映射了,而是直接“曲线救国”,加了一个跨层连接 恒等映射。
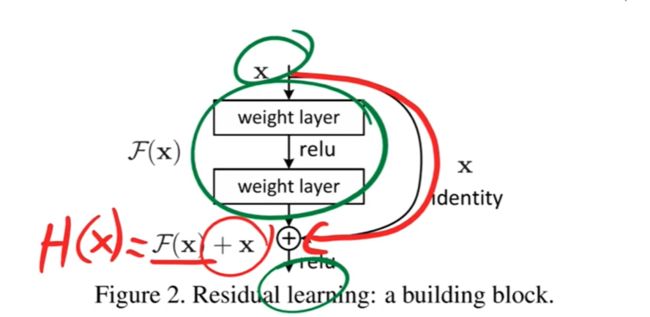
绿色圆圈的网络 F ( x ) F(x) F(x) 只是学习什么东西让输出和输入不同并且学习差异。在权重层趋向于零函数之前,我们对权重层使用权重衰减,或通常我们如何初始化它们,它们会很好地趋向于零函数。
如果 F ( x ) F(x) F(x) 趋向于0函数,那么 H ( x ) H(x) H(x) 成为恒等函数。