初探图神经网络——GNN
title: 图神经网络(GNN)
date:
tags:
- 随笔
- 知识点
categories: - [学习笔记]
初探图神经网络(GNN)
文章来源:https://distill.pub/2021/gnn-intro/
前言:说一下为什么要写这篇文章,因为自己最近一直听说“图神经网络”,但是一直不了解这是什么,因此这次有机会对图神经网络有一个简单的认识了解好了,开始步入正题。
整片文章并没有对内容进行章节部分的划分,只是从头到尾进行了讲解,因此这里就根据原文的顺序依次做笔记的填写了。
文章首先说了这样的一句话We are starting to see.....。这句话的提出就说明了现在的图神经网络还是正在兴起的阶段,因此还是有一定的发展前景的——既是挑战也是机遇。
作者从以下四个方面来说明和解释什么是图神经网络(也是本文的主要讲述的点):
- 什么样子的数据可以表示成为图;
- 图跟其他的数据有什么不一样的地方;
- 构建一个GNN;
- 提供一个GNN playground;
什么是图
图表示实体节点之间的关系,如下图所示:
其中U表示的是整张图。
为了进一步说明什么是节点、关系和整张图,我们可以用下面的方式来表示出什么是图(用向量的方式来表示出):
![]()
另外,图可以表示为无向图和有向图两种图:
数据表示成图
那么其他的数据是怎么可以表示成图的呢?
Imgae as graphs
我们将图片数据的像素点看成是一个节点,这样的话就可以构造出一个图:
Text as graphs
用图来表示一段文本的话,那就是一个有向图来表示了,那么一段话中,每一个字符、单词、token等都可以作为图的节点:
当然,文章也说明了,目前来说的图片和文本用图的形式来表示的话,并非是两者常用的编码方法,因为用图的形式来表示的话,会产生冗余的表示形式。
其他形式的数据表示
- 比赛关系的表示(简单说一下这个例子:就是在跆拳道比赛中,每个人与其他人比赛之间的关系——是否进行比赛,可以用图的形式来表示):
解决的问题方向或应用
那么图可以解决什么问题呢,可以从以下三个方面来考虑:
- 图层面(graph-level)
- 节点层面(node-level)
- 边层面(edge-level)
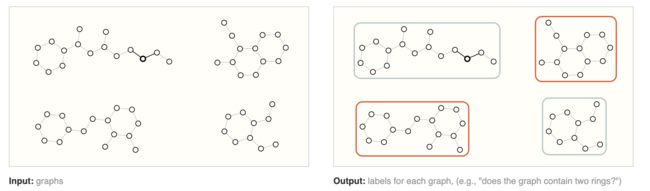
首先是图层面的任务,文章中说到了一个任务就是查看或者说检查一个分子图中是否存在两个环:
这类问题在图像中与分类问题很像,在文本中与情感分析的任务很想。
节点层面的任务,文中所举的例子是跆拳道的比赛问题——假设在比赛过程中指导员Mr. Hi和管理员John H产生了分歧,节点表示参与竞赛的人员,边表示关系,那么任务就是——正确分类参与人员是Mr. Hi一方的人还是John H一方的人:
![]()
那么在图像中,就类似是图像的分割任务,每一个节点代表是一个像素;
在文本中,就类似预测句子中的单词的词性——词性标注;
那么边层面上考虑,文中提出了这样一个场景——假设在一场比赛中,人物都用节点来表示,那么边就用来表示节点之间的关系:
也就是说,任务转为预测节点之间的关系,那么就很像是知识图谱中的关系抽取一样的作用:
在机器学习中存在的问题
文章主要是针对在神经网络中存在的问题做了论述,即将神经网络用到图上该怎么表示图。
到目前,我们知道图有四种属性是需要我们来考虑的:
- 节点;
- 边;
- 全图属性信息;
- 连接性
前三个还可以表示——用向量来表示,最难来表示的就是最后一个——图的连接性,即如何来表示两个节点的连通性呢?
有人说可以用邻接矩阵来实现连通性的存储表示,但是这样会存在一些问题:
-
数据量很大的前提下 ,图是存储不了的;
-
如果用稀疏矩阵来表示地话,在GPU上计算是不能实现并行计算的(这也是目前来说待解决的问题);
-
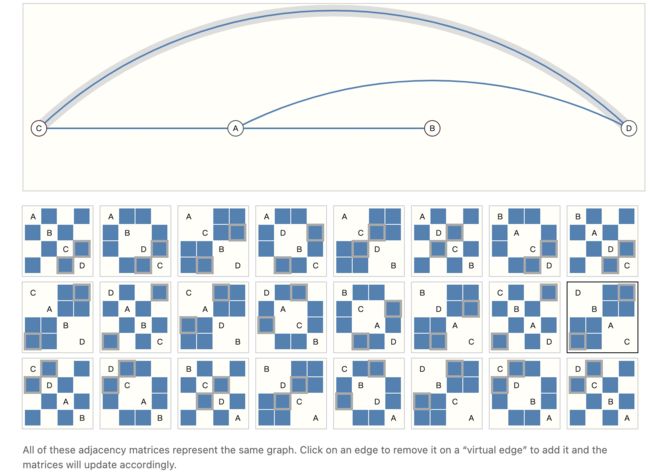
邻接矩阵还有一个特点就是——一个图的信息可以用不同的邻接矩阵来表示,那么针对不同的数据的输入,神经网络该如何处理呢?也就是如何处理数据来实现无顺序性的表示。
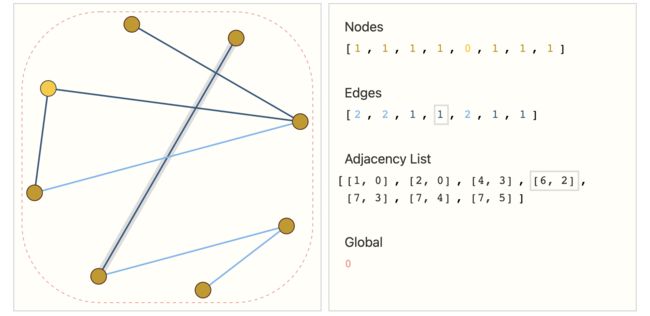
文中提出了下面这样的表示方法:
- 对于图中的节点,用一个标量来表示(将图中的节点进行编号),类似One-hot的表示方法;
- 对于图中的边,也用一个标量来表示,同样地还是用类似One-hot的方法来表示;
- 这里的连接性用邻接列表来表示,列表的长度代表来边的个数,列表中的元素是一个二元组,分别表示的是边的两边联通的是哪两个节点;
图神经网络是什么?
文中先是给出了一个GNN的概念:
A GNN is an optimizable transformation on all attributes of the graph (nodes, edges, global-context) that preserves graph symmetries (permutation invariances).
翻译过来就是,图神经网络是一个能够在图的属性上进行转换,且能够保持图上的对称信息的。
对称信息的意思就是,将节点的位置进行重新打乱排序之后,图的结构还是不变的。
文中说使用了message passing neural network框架来进行构建GNN,当然还有其他的网络来进行表示。在该网络中,输入的是一个图网络,输出的还是一个图网络。
The simplest GNN
我们来构造一个最简单的GNN的例子,如下图所示,对于顶点向量(也就是我们前面提到的节点向量),边向量和全局向量,我们分别构造一个多层感知机。
这样三个MLP就构成了一个GNN的层。
这个层的作用就是根据输入的顶点向量、边向量和全局向量,对应地输入到MLP中,然后输入对应的图,其中只是图的属性做出了改变,但是联通性或者说结构没有发生改变。
如何预测
那么接下来就考虑,如何去预测了?
- 简单情况
先考虑最简单的二分类问题,对于顶点我们已经有了全部的顶点向量信息,通过这些顶点向量信息我们可以在其后面追加一个输出大小为2的全连接层,最后再用一个softmax做一个分类即可;
同样地,对于一个多分类问题,也是只需要在输出后面添加一个输出大小为n的全连接层,最后添加一个softmax作为预测即可。
对于线性回归问题,只需要一个输出大小为1的连接层即可。
下图的意思就是,给定最后一层的输出(是一个图),然后将顶点输入到全连接层中,最后得到预测的输出。
需要注意的是,所有的节点都共享同一个全连接层的参数;同理,所有的边也是共享同一个全连接层的参数。
- 复杂情况
如果没有顶点信息,但是仍然需要做顶点的情况预测,那么该怎么处理呢?
文中提到了一种方法就是——Pooling,该方法分两步:
- 对于需要被pool的元素(这里的元素是指与没有顶点信息相邻的边),收集它们向量表示;
- 对于收集到的全部向量做加法求和,得到一个新的向量,此时这个向量就是我们要求得的顶点向量;
- (其中还需要添加一个全局向量,但是文中并未提及,但是会在全局信息的共享中说明这个东西是什么)
用公式的方法来表示的话,就是用下图来表示:
上图中是说没有点,只有边的情况,那么对于只有点信息没有边的情况,那么可以用下面的方法来表示:
因此,针对于上述的方法,我们可以看出,不管缺少哪种数据,我们都可以根据pool的方法来获得缺少的数据。
那么总结一个简单的GNN,就用下图来表示,先是输入一个图,然后通过MLP,得到最后的输出,如果缺少了数据,可以用pooling层来处理,然后再经过分类层得到最后的预测结果。
![]()
信息传递
上述的方法有一个很大的局限性就是不能够利用图的结构信息来预测,可以看出上述的方法只是分别独立地对于点,边,全局信息作属性的修改,没有利用连接关系,那信息传递就可以很好地来解决这个问题。
其实消息传递的过程跟pooling的过程很是相似,过程可以用下图来表示(用相邻的节点信息来加和):
用公式化的形式表示如下:
前面讲到的pooling都是在最后的输出层之后做的,那么是否可以根据这个方法来提前对属性进行补全呢?
答案是可以的。
下面是根据这个方法,可以将图中点和边的信息进行共享分布,本质上还是向量的相加(都是相邻的才能相加,换句话说就是只有是相邻与点V相连的边才能加到把点V的向量加到边上,同理边加到点上的道理也一样。)
但是呢,究竟是先从点集加到边集好,还是先从边集加到点集好(两种方法会产生不一样的结果),尚未有定论。另外文中还给出了其他的方法,比如交替汇聚pool,这里就不做论述了。
全局信息的共享
到目前为止,我们所讨论的情况是存在这样的一个问题:无法共享不直接相邻点或边的信息。
这就是我们为什么要引入全局变量这个信息或概念的原因。
文中提出的说到方法就是引入一个图U——被称作master node或context vector.这个U,连接了图中所有的边和点,因此可以作为信息传递的桥梁,具体来说可以用下图来表示:
![]()
搭建一个GNN
这一部分就是在文中有一个交互图了,体现了GNN对超参数的调整是很敏感的,虽然也不清楚图表示的是什么意思,在这里就不做阐述了。
文章后面还做了大量的讨论,有时间再补上吧。