11.动态规划：树形DP问题、树上最大独立集【灵神基础精讲】

树形DP问题

回溯和树形DP的区别（什么时候需要return结果？）：对于回溯，通常是在「递」的过程中增量地构建答案，并在失败时能够回退，例如八皇后。对于递归，是把原问题分解为若干个相似的子问题，通常会在「归」的过程中有一些计算。如果一个递归能考虑用记忆化来优化，就需要 return 一个值并加以保存。

一、树的直径（二叉树==>一般树）

树形DP①树的直径【基础算法精讲 23】

二叉树的直径：

• 复习：104. 二叉树的最大深度

• 边权型： 543. 二叉树的直径

• 点权型： 124. 二叉树的最大路径和

一般树的直径：

• 1245.树的直径
• 2246.相邻字符不同的最长路径

---

一篇文章解决所有二叉树路径问题：https://leetcode.cn/problems/diameter-of-binary-tree/solution/yi-pian-wen-zhang-jie-jue-suo-you-er-cha-6g00/

二叉树路径的问题大致可以分为两类：

一、自顶向下：这类题通常用深度优先搜索(DFS)和广度优先搜索(BFS)解决

二、非自顶而下：这类题目一般解题思路如下：设计一个辅助函数dfs调用自身求出以一个节点为根节点的左侧最长路径left和右侧最长路径right，那么经过该节点的最长路径就是left+right
接着只需要从根节点开始dfs,不断比较更新全局变量即可

这类题型DFS注意点：

1、left,right代表的含义要根据题目所求设置，比如最长路径、最大路径和等等

2、全局变量res的初值设置是0还是INT_MIN要看题目节点是否存在负值,如果存在就用INT_MIN，否则就是0

3、注意两点之间路径为1，因此一个点是不能构成路径的

543. 二叉树的直径

难度简单1303

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树

          1
         / \
        2   3
       / \     
      4   5    

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

**注意：**两结点之间的路径长度是以它们之间边的数目表示。

题解：

换个角度看直径

从一个叶子出发向上，在某个节点[拐弯]，向下到达另一个叶子得到了由两条链拼起来的路径。(也可能只有一条链)

算法

遍历二叉树，在计算最长链的同时，顺带把直径算出来。

• 在当前节点[拐弯]的直径长度 =左子的最长链 +右子的最长链 +2

• 返回给父节点的是以当前节点为根的子树的最长链-max(左子树的最长链，右子树的最长链)+1。

class Solution {
    int res = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        dfs(root);
        return res;
    }

    // private int dfs(TreeNode root){
    //     if(root.left == null && root.right == null){
    //         return 0; //不能是root == null 
    //     }
    //     // 获得左右子树的最长路径
    //     int left = root.left == null ? 0 : dfs(root.left) + 1;
    //     int right = root.right == null ? 0 : dfs(root.right) + 1;
    //     res = Math.max(res, left + right); 
    //     return Math.max(left, right); // 返回左右子树长度较长的那一个
    // }
    //零神写法：
    public int dfs(TreeNode node){
        if(node == null) 
            return -1; // 下面 +1 后，对于叶子节点就刚好是 0
        int leftlen = dfs(node.left) + 1; // 左子树最大链长+1
        int rightlen = dfs(node.right) + 1; // 右子树最大链长+1
        res = Math.max(res, leftlen + rightlen); // 两条链拼成路径
        return Math.max(leftlen, rightlen); // 当前子树最大链长
    }
}

124. 二叉树中的最大路径和

难度困难1919

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

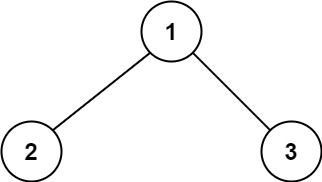
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

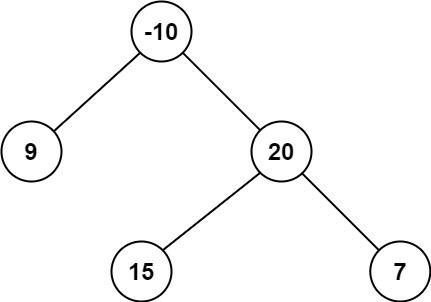
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

• 树中节点数目范围是 [1, 3 * 104]
• -1000 <= Node.val <= 1000

题解：从边变成了点，实际上解法是一样的

算法：

遍历二叉树，在计算最大链和的同时，顺带更新答案的最大值。

在当前节点[拐弯]的最大路径和= 左子树最大链和 + 右子最大链和 +当前节点值。

返回给父节点的是 max(左子树最大链和，右子树最大链和)+ 当前节点值，如果这个值是负数，则返回 0。

class Solution {
    int res = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
        dfs(root);
        return res;
    }

    public int dfs(TreeNode node){
        if(node == null) 
            return 0;
        int leftlen = dfs(node.left);
        int rightlen = dfs(node.right);
        res = Math.max(res, leftlen + rightlen + node.val);
        return Math.max(0, Math.max(leftlen, rightlen) + node.val);
    }
}

(树的直径)2246. 相邻字符不同的最长路径

难度困难50

给你一棵 树（即一个连通、无向、无环图），根节点是节点 0 ，这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树，其中 parent[i] 是节点 i 的父节点，由于节点 0 是根节点，所以 parent[0] == -1 。

另给你一个字符串 s ，长度也是 n ，其中 s[i] 表示分配给节点 i 的字符。

请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ，并返回该路径的长度。

示例 1：

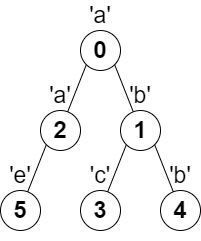
输入：parent = [-1,0,0,1,1,2], s = "abacbe"
输出：3
解释：任意一对相邻节点字符都不同的最长路径是：0 -> 1 -> 3 。该路径的长度是 3 ，所以返回 3 。
可以证明不存在满足上述条件且比 3 更长的路径。 

示例 2：

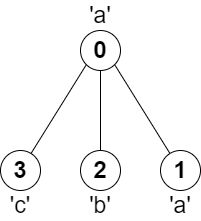
输入：parent = [-1,0,0,0], s = "aabc"
输出：3
解释：任意一对相邻节点字符都不同的最长路径是：2 -> 0 -> 3 。该路径的长度为 3 ，所以返回 3 。

提示：

• n == parent.length == s.length
• 1 <= n <= 105
• 对所有 i >= 1 ，0 <= parent[i] <= n - 1 均成立
• parent[0] == -1
• parent 表示一棵有效的树
• s 仅由小写英文字母组成

思考：

1、如何求树的直径？

• 思路一: 遍历 x 的子树，把最长链的长度都存到一个列表中，排序，取最大的两个

• 思路二: 遍历 x 的子树的同时求最长+次长

↓↓↓↓↓↓

2、如何一次遍历找到最长+次长?

• 如果次长在前面，最长在后面那么遍历到最长的时候就能算出最长+次长
• 如果最长在前面，次长在后面那么遍历到次长的时候就能算出最长+次长

一、求树的直径（本题是以parent数组表示的图）

• 求树的直径-树形DP模板

class Solution {
    List<Integer>[] g;
    String s;
    int ans;
    public int longestPath(int[] parent, String s) {
        this.s = s;
        int n = parent.length;
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int i = 1; i < n; i++)
            g[parent[i]].add(i);
        dfs(0);
        return ans + 1; // 求点的个数 = 边个数 + 1
    }

    public int dfs(int x){
        int maxlen = 0;// 记录x的最大链长
        for(int y : g[x]){
            int len = dfs(y) + 1;	// y为根节点的最大链长
            ans = Math.max(ans, maxlen + len); // 更新答案的最大链长（xy分别为最长和次长时的直径）
            maxlen = Math.max(maxlen, len); // 更新 x 的最大链长
        }
        return maxlen; // 返回x的最大链长
    }
}

二、2246题的解法

• 在求树的直径问题上加判断条件

class Solution {
    List<Integer>[] g;
    String s;
    int ans;
    public int longestPath(int[] parent, String s) {
        this.s = s;
        int n = parent.length;
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int i = 1; i < n; i++)
            g[parent[i]].add(i);
        dfs(0);
        return ans + 1; // 求点的个数 = 边个数 + 1
    }

    public int dfs(int x){
        int maxlen = 0;
        for(int y : g[x]){
            int len = dfs(y) + 1;
            // 条件：相邻节点不能分配到相同字符
            if(s.charAt(y) != s.charAt(x)){
                ans = Math.max(ans, maxlen + len); // 更新答案的最大链长
                maxlen = Math.max(maxlen, len); // 更新 x 的最大链长
            }   
        }
        return maxlen; // 返回x的最大链长
    }
}

如果x的邻居包含父节点(x节点)，在DFS中额外传入参数表示父节点：

class Solution {
    List<Integer>[] g;
    String s;
    int ans;
    public int longestPath(int[] parent, String s) {
        this.s = s;
        int n = parent.length;
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int i = 1; i < n; i++)
            g[parent[i]].add(i);
        dfs(0, -1);
        return ans + 1;
    }

    public int dfs(int x, int fa){
        int maxlen = 0;
        for(int y : g[x]){
            if(y == fa) continue; // y是x的父节点就跳过
            int len = dfs(y, x) + 1;
            // 条件：相邻节点不能分配到相同字符
            if(s.charAt(y) != s.charAt(x)){
                ans = Math.max(ans, maxlen + len); // 更新答案的最大链长
                maxlen = Math.max(maxlen, len); // 更新 x 的最大链长
            }   
        }
        return maxlen; // 返回x的节点个数
    }
}

二、树上最大独立集（打家劫舍Ⅲ）

树形DP如何思考？打家劫舍III【基础算法精讲 24】

树的最大独立集合：对于一颗无根树，选出尽量多的点使得任何两个结点均不相邻。

337. 打家劫舍 III

难度中等1682

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

提示：

• 树的节点数在 [1, 104] 范围内
• 0 <= Node.val <= 104

题解：

1、选或不选

• 选当前节点：左右儿子都不能选

• 不选当前节点：左右儿子可选可不选

2、提炼状态

• 选当前节点时，以当前节点为根的子树最大点权和

• 不选当前节点时，以当前节点为根的子树最大点权和

3、转移方程

• 选 = 左不选 + 右不选 + 当前节点值

• 不选 =max(左选，左不选) + max(右选，右不选)

最终答案=max(根选，根不选）

class Solution {
    public int rob(TreeNode root) {
        int[] res = dfs(root);
        return Math.max(res[0], res[1]);
    }
    //   当前结点值：
    // res[0] : 选 = 左不选 + 右不选 + 当前节点值
    // res[1] : 不选 = max(左选,左不选) + max(右选,右不选)
    public int[] dfs(TreeNode node){
        if(node == null)
            return new int[]{0, 0};
        int[] left = dfs(node.left);
        int[] right = dfs(node.right);
        int[] res = new int[2];
        res[0] = left[1] + right[1] + node.val;
        res[1] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        return res;
    }
}

课后作业： 没有上司的舞会 https://www.luogu.com.cn/problem/P1352 1377. T 秒后青蛙的位置 https://leetcode.cn/problems/frog-position-after-t-seconds/ 1377 思考题：如果有多个目标位置呢？ 2646. 最小化旅行的价格总和 https://leetcode.cn/problems/minimize-the-total-price-of-the-trips/

三、树上最小支配集

练习

1.树的直径相关问题

687. 最长同值路径

难度中等762

给定一个二叉树的 root ，返回 最长的路径的长度 ，这个路径中的 每个节点具有相同值 。 这条路径可以经过也可以不经过根节点。

两个节点之间的路径长度 由它们之间的边数表示。

示例 1:

输入：root = [5,4,5,1,1,5]
输出：2

示例 2:

输入：root = [1,4,5,4,4,5]
输出：2

提示:

• 树的节点数的范围是 [0, 104]
• -1000 <= Node.val <= 1000
• 树的深度将不超过 1000

class Solution {
    int res = 0;
    public int longestUnivaluePath(TreeNode root) {
        dfs(root);
        return res;
    }

    public int dfs(TreeNode node){
        if(node == null) 
            return -1; // 下面 +1 后，对于叶子节点就刚好是 0
        int leftlen = dfs(node.left) + 1; // 左子树最大链长+1
        int rightlen = dfs(node.right) + 1; // 右子树最大链长+1

        // 如果当前节点的值与左/右子树的值不同，链长可视作0
        if(node.left != null && node.left.val != node.val) leftlen = 0;
        if(node.right != null && node.right.val != node.val) rightlen = 0;
        
        res = Math.max(res, leftlen + rightlen); // 两条链拼成路径
        return Math.max(leftlen, rightlen); // 当前子树最大链长
    }
}

---

1617. 统计子树中城市之间最大距离

难度困难149

给你 n 个城市，编号为从 1 到 n 。同时给你一个大小为 n-1 的数组 edges ，其中 edges[i] = [ui, vi] 表示城市 ui 和 vi 之间有一条双向边。题目保证任意城市之间只有唯一的一条路径。换句话说，所有城市形成了一棵 树 。

一棵 子树 是城市的一个子集，且子集中任意城市之间可以通过子集中的其他城市和边到达。两个子树被认为不一样的条件是至少有一个城市在其中一棵子树中存在，但在另一棵子树中不存在。

对于 d 从 1 到 n-1 ，请你找到城市间 最大距离 恰好为 d 的所有子树数目。

请你返回一个大小为 n-1 的数组，其中第 d 个元素（下标从 1 开始）是城市间 最大距离 恰好等于 d 的子树数目。

请注意，两个城市间距离定义为它们之间需要经过的边的数目。

示例 1：

输入：n = 4, edges = [[1,2],[2,3],[2,4]]
输出：[3,4,0]
解释：
子树 {1,2}, {2,3} 和 {2,4} 最大距离都是 1 。
子树 {1,2,3}, {1,2,4}, {2,3,4} 和 {1,2,3,4} 最大距离都为 2 。
不存在城市间最大距离为 3 的子树。

示例 2：

输入：n = 2, edges = [[1,2]]
输出：[1]

示例 3：

输入：n = 3, edges = [[1,2],[2,3]]
输出：[2,1]

提示：

• 2 <= n <= 15
• edges.length == n-1
• edges[i].length == 2
• 1 <= ui, vi <= n
• 题目保证 (ui, vi) 所表示的边互不相同。

本题结合了 78 题和 1245 题：枚举城市的子集（子树），求这棵子树的直径。

需要注意的是，枚举的子集不一定是一棵树，可能是森林（多棵树，多个连通块）。我们可以在计算树形 DP 的同时去统计访问过的点，看看是否与子集相等，只有相等才是一棵树。

class Solution {
    int[] res;
    boolean[] inSet, vis;
    int n, diameter;
    List<Integer>[] g;
    public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {
        res = new int[n-1];
        g = new ArrayList[n];
        inSet = new boolean[n];
        this.n = n;
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int[] e : edges){
            int x = e[0] - 1, y = e[1] - 1;
            g[x].add(y);
            g[y].add(x);
        }
        f(0); // 回溯：枚举所有子集的可能性
        return res;
    }
    // 枚举所有子树的可能性（子集型回溯）
    public void f(int i){
        if(i == n){
            // 枚举的子集不一定是一棵树，可能是森林
            for(int v = 0; v < n; v++){
                if(inSet[v]){
                    vis = new boolean[n];
                    diameter = 0;
                    dfs(v);
                    break;
                }
            }
            if(diameter > 0 && Arrays.equals(vis, inSet)){
                ++res[diameter-1];
            }
            return;
        }
        f(i+1); // 不选城市i
        // 选城市i
        inSet[i] = true;
        f(i+1);
        inSet[i] = false;
    }

    // 求树的直径
    public int dfs(int x){
        vis[x] = true;
        int maxLen = 0;
        for(int y : g[x]){
            if(!vis[y] && inSet[y]){
                int ml = dfs(y) + 1;
                diameter = Math.max(diameter, maxLen + ml);
                maxLen = Math.max(maxLen, ml);
            }
        }
        return maxLen;
    }
}

---

2538. 最大价值和与最小价值和的差值

难度困难33

给你一个 n 个节点的无向无根图，节点编号为 0 到 n - 1 。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。

每个节点都有一个价值。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价值。

一条路径的 价值和 是这条路径上所有节点的价值之和。

你可以选择树中任意一个节点作为根节点 root 。选择 root 为根的 开销 是以 root 为起点的所有路径中，价值和 最大的一条路径与最小的一条路径的差值。

请你返回所有节点作为根节点的选择中，最大 的 开销 为多少。

示例 1：

输入：n = 6, edges = [[0,1],[1,2],[1,3],[3,4],[3,5]], price = [9,8,7,6,10,5]
输出：24
解释：上图展示了以节点 2 为根的树。左图（红色的节点）是最大价值和路径，右图（蓝色的节点）是最小价值和路径。
- 第一条路径节点为 [2,1,3,4]：价值为 [7,8,6,10] ，价值和为 31 。
- 第二条路径节点为 [2] ，价值为 [7] 。
最大路径和与最小路径和的差值为 24 。24 是所有方案中的最大开销。

示例 2：

输入：n = 3, edges = [[0,1],[1,2]], price = [1,1,1]
输出：2
解释：上图展示了以节点 0 为根的树。左图（红色的节点）是最大价值和路径，右图（蓝色的节点）是最小价值和路径。
- 第一条路径包含节点 [0,1,2]：价值为 [1,1,1] ，价值和为 3 。
- 第二条路径节点为 [0] ，价值为 [1] 。
最大路径和与最小路径和的差值为 2 。2 是所有方案中的最大开销。

提示：

• 1 <= n <= 105
• edges.length == n - 1
• 0 <= ai, bi <= n - 1
• edges 表示一棵符合题面要求的树。
• price.length == n
• 1 <= price[i] <= 105

题解：0x3f：https://leetcode.cn/problems/difference-between-maximum-and-minimum-price-sum/solution/by-endlesscheng-5l70/

1、由于价值都是正数，因此价值和最小的一条路径一定只有一个点。

2、根据提示 1，「价值和最大的一条路径与最小的一条路径的差值」等价于「去掉路径的一个端点」。

3、由于价值都是正数，一条路径能延长就尽量延长，这样路径和就越大，那么最优是延长到叶子。根据提示 2，问题转换成去掉一个叶子后的最大路径和（这里的叶子严格来说是度为 1 的点，因为根的度数也可能是 1）。

4、最大路径和是一个经典树形 DP 问题，类似「树的直径」。由于我们需要去掉一个叶子，那么可以让子树返回两个值：

• 带叶子的最大路径和；

• 不带叶子的最大路径和。

对于当前节点，它有多颗子树，我们一颗颗 DFS，假设当前 DFS 完了其中一颗子树，它返回了「当前带叶子的路径和」和「当前不带叶子的路径和」，那么答案有两种情况：

• 前面最大带叶子的路径和 + 当前不带叶子的路径和；

• 前面最大不带叶子的路径和 + 当前带叶子的路径和；

然后更新「最大带叶子的路径和」和「最大不带叶子的路径和」。

最后返回「最大带叶子的路径和」和「最大不带叶子的路径和」，用来供父节点计算。

class Solution {
    List<Integer>[] g;
    int n;
    long res;
    int[] price;
    public long maxOutput(int n, int[][] edges, int[] price) {
        this.n = n;
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int[] e : edges){
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x);
        }
        this.price = price;
        dfs(0, -1);
        return res;
    }

    // 返回带叶子的最大路径和，不带叶子的最大路径和
    public long[] dfs(int x, int fa){
        // s1 带叶子的最大路径和 ； s2 不带叶子的最大路径和
        long p = price[x], maxS1 = p, maxS2 = 0;
        for(int y : g[x]){
            if(y != fa){
                long[] result = dfs(y, x);
                long s1 = result[0], s2 = result[1];
                // 前面最大带叶子的路径和 + 当前不带叶子的路径和
                // 前面最大不带叶子的路径和 + 当前带叶子的路径和
                res = Math.max(res, Math.max(maxS1 + s2, maxS2 + s1));
                // 这里加上 p 是因为 x 必然不是叶子
                maxS1 = Math.max(maxS1, s1 + p);
                maxS2 = Math.max(maxS2, s2 + p);
            }
        }
        return new long[]{maxS1, maxS2};
    }
}

2.树上最大独立集练习题

P1352 没有上司的舞会

题目描述

某大学有 $n$ 个职员，编号为 $1\dots n$。

他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。

现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数 $r_i$，但是呢，如果某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。

所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

输入格式

输入的第一行是一个整数 $n$。

第 $2$ 到第 $(n+1)$ 行，每行一个整数，第 $(i+1)$ 行的整数表示 $i$ 号职员的快乐指数 $r_i$。

第 $(n+2)$ 到第 $2n$ 行，每行输入一对整数 $l,k$，代表 $k$ 是 $l$ 的直接上司。

输出格式

输出一行一个整数代表最大的快乐指数。

样例 #1

样例输入 #1

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5

样例输出 #1

5

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le n\le 6\times 10^3$，$-128\le r_i\le 127$，$1\le l,k\le n$，且给出的关系一定是一棵树。

public class test {

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        int n = Integer.valueOf(br.readLine());
        int[] nums = new int[n];
        for (int i = 0; i < n; i++) {
            nums[i] = Integer.valueOf(br.readLine());
        }
        // 入度 + 1，出度 - 1，根据最大入度找根节点
        int[] degree = new int[n];
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (int i = 0; i < n - 1; i++) {
            String[] strs = br.readLine().split(" ");
            int x = Integer.valueOf(strs[0]) - 1;
            int y = Integer.valueOf(strs[1]) - 1;
            g[y].add(x);
            degree[y] += 1;
            degree[x] -= 1;
        }
        int fa = 0;
        for (int i = 0; i < n; i++) {
            if (degree[i] > degree[fa])
                fa = i;
        }
        int[] res = dfs(fa, g, nums);
        out.println(Math.max(res[0], res[1]));
        out.flush();
    }

    // res[0] : 选 = 左不选 + 右不选 + 当前节点值
    // res[1] : 不选 = max(左选,左不选) + max(右选,右不选)
    public static int[] dfs(int i, List<Integer>[] g, int[] nums) {
        if (g[i].size() == 0)
            return new int[] { 1, 0 };
        int[] res = new int[2];
        for (int y : g[i]) {
            int[] child = dfs(y, g, nums);
            res[0] += child[1];
            res[1] += Math.max(child[0], child[1]);
        }
        res[0] += nums[i];
        return res;
    }
}

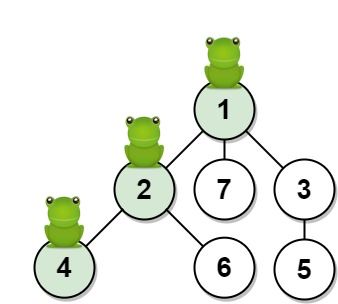
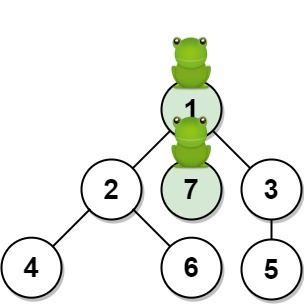
1377. T 秒后青蛙的位置

难度困难103

给你一棵由 n 个顶点组成的无向树，顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下：

• 在一秒内，青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点（如果它们直接相连）。
• 青蛙无法跳回已经访问过的顶点。
• 如果青蛙可以跳到多个不同顶点，那么它跳到其中任意一个顶点上的机率都相同。
• 如果青蛙不能跳到任何未访问过的顶点上，那么它每次跳跃都会停留在原地。

无向树的边用数组 edges 描述，其中 edges[i] = [ai, bi] 意味着存在一条直接连通 ai 和 bi 两个顶点的边。

返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10-5 的结果将被视为正确答案。

示例 1：

输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出：0.16666666666666666 
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，第 1 秒 有 1/3 的概率跳到顶点 2 ，然后第 2 秒 有 1/2 的概率跳到顶点 4，因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。 

示例 2：

输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出：0.3333333333333333
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。 

提示：

• 1 <= n <= 100
• edges.length == n - 1
• edges[i].length == 2
• 1 <= ai, bi <= n
• 1 <= t <= 50
• 1 <= target <= n

https://blog.csdn.net/qq_42958831/article/details/130839438

https://leetcode.cn/problems/frog-position-after-t-seconds/solution/dfs-ji-yi-ci-you-qu-de-hack-by-endlessch-jtsr/

既然答案是由若干分子为 1 的分数相乘得到，那么干脆只把分母相乘，最后再计算一下倒数，就可以避免因浮点乘法导致的精度丢失了。另外，整数的计算效率通常比浮点数的高。

• 自顶向下是一边[递]，一边把儿子个数 c 乘起来，如果能在第 t 秒到达 target，或者小于t 秒到达 target 且 target 是叶子节点(此时每次跳跃都会停留在原地) ，那么就记录答案为乘积的倒数，同时返回一个布尔值表示递归结束
• 自底向上的思路是类似的，找到 target 后，在[归]的过程中做乘法。 个人更喜欢这种写法，因为只在找到 target 之后才做乘法，而自顶向下即使在不含 target 的子树中搜索，也会盲目地做乘法。

技巧：
可以把节点 1 添加一个 0 号邻居，从而避免判断当前节点为根节点1，也避免了特判 n = 1的情况

此外，DFS 中的时间不是从 0 开始增加到 t，而是从 leftT = t 开始减小到 0，这样代码中只需和 0 比较，无需和 t 比较，从而减少一个DFS 之外变量的引入。

方法一：自顶向下

class Solution {
    List<Integer>[] g;
    double ans = 0.0;
    int target;
    public double frogPosition(int n, int[][] edges, int t, int target) {
        this.target = target;
        g = new ArrayList[n+1];
        Arrays.setAll(g, e -> new ArrayList<>());
        g[1].add(0);
        for(int[] e : edges){
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x);
        }
        dfs(1, 0, t, 1);
        return ans;
    }

    public boolean dfs(int x, int fa, int left_time, long prod){
        // t 秒后必须在 target（恰好到达，或者 target 是叶子停在原地）
        if(x == target && (left_time == 0 || g[x].size() == 1)){
            ans = 1.0 / prod;
            return true;
        }
        if(x == target || left_time == 0) return false;
        for(int y : g[x]){ // 遍历 x 的儿子 y
            if(y != fa && dfs(y, x, left_time-1, prod * (g[x].size() - 1)))
                return true; // 找到 target 就不再递归了
        }
        return false; // 未找到target
    }
}

方法二：自底向上

class Solution {
    List<Integer>[] g;
    int target;
    public double frogPosition(int n, int[][] edges, int t, int target) {
        this.target = target;
        g = new ArrayList[n+1];
        Arrays.setAll(g, e -> new ArrayList<>());
        g[1].add(0);
        for(int[] e : edges){
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x);
        }
        long prod = dfs(1, 0, t);
        return prod != 0 ? 1.0 / prod : 0;
    }

    public long dfs(int x, int fa, int left_time){
        if(left_time == 0)
            return x == target ? 1 : 0;
        if(x == target) 
            return g[x].size() == 1 ? 1 : 0;
        for(int y : g[x]){
            if(y != fa){
                long prod = dfs(y, x, left_time-1); // 寻找 target
                if(prod != 0){
                    return prod * (g[x].size() - 1); // 乘上儿子个数，并直接返回
                }
            }
        }
        return 0; // 未找到target
    }
}

2646. 最小化旅行的价格总和

难度困难29

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：

输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

示例 2：

输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。 
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。 
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

提示：

• 1 <= n <= 50
• edges.length == n - 1
• 0 <= ai, bi <= n - 1
• edges 表示一棵有效的树
• price.length == n
• price[i] 是一个偶数
• 1 <= price[i] <= 1000
• 1 <= trips.length <= 100
• 0 <= starti, endi <= n - 1

class Solution {
    // 1. 计算每个点经过的次数 cnt（贡献法思想：计算每个点对答案能贡献多少）
    // 2. 写一个树形DP求答案
    private List<Integer>[] g;
    private int[] price, cnt;
    private int end;

    public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int[] e : edges){
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x); // 建树
        }
        this.price = price;

        // 1. 计算每个点经过的次数 cnt
        cnt = new int[n];
        for(int[] t : trips){
            end = t[1];
            path(t[0], -1);
        }
        // 2. 写一个树形DP求答案
        // 随便选一个点出发进行DP就可以了
        // 为什么？题目的描述与根节点无关
        int[] p = dfs(0, -1); 
        return Math.min(p[0], p[1]);

    }
    // 寻找路径，找到终点就返回True（注意树只有唯一的一条简单路径）
    // 寻找路径的同时标记源点到终点所有的点 +1
    private boolean path(int x, int fa) {
        if(x == end){ // 到达终点
            cnt[x]++; // 统计从 start 到 end 的路径上的点经过了多少次
            return true;
        }
        for(int y : g[x]){
            if(y != fa && path(y,x)){
                cnt[x]++; // 统计从 start 到 end 的路径上的点经过了多少次
                return true; // 找到终点
            }
        }
        return false; // 未找到终点
    }

    private int[] dfs(int x, int fa){
        int notHalve = price[x] * cnt[x]; // x 不变
        int halve = notHalve / 2; // x 减半
        for(int y : g[x]){
            if(y != fa){
                int[] p = dfs(y, x); // 计算 y 不变/减半的最小价值总和
                // x没有减半的话，y既可以减半，也可以不减半，取这两种情况的最小值
                notHalve += Math.min(p[0], p[1]);
                halve += p[0]; // x 减半，那么 y 只能不变
            }
        }
        return new int[]{notHalve, halve};
    }
}