5、学习率、过拟合

知识补充

在上个博客中，我们已经学会对参数进行训练。但是我们的学习率learn_rate是固定的，这就会出现一个问题。我们将参数进行某个方向上的梯度下降,没训练一次，下降一次，因为学习率是固定的，所以我们下降的高度也是一样的。如果，我们下降到了对低点上面一点，我们再下降一次，过了最低点，又上去了。这就很尴尬了。再继续训练下去，只会在最低点周围反复横跳。永远达不到最低点。关键在于学习率，我们在一次训练结束后，要对学习率进行一个调整。至于怎么调整？我们可以观察学习率与误差的关系，因为学习率越合适，误差就是越小。然后找到一个最优点。注意，最优点不一定是最低点。一般是取偏上面的一个点。因为对这一组数据，这个点是最低点，但是换了另外一组数据可能就不是了。

1. 定义数据集的误差和精确度

代码如下所示：

def valid_loss(parameters):
    loss_accu = 0
    for img_i in range(valid_num):
        loss_accu+=sqr_loss(valid_img[img_i],valid_lab[img_i],parameters)
    return loss_accu/(valid_num/10000)
def valid_accuracy(parameters):
    correct = [predict(valid_img[img_i],parameters).argmax()==valid_lab[img_i] for img_i in range(valid_num) ]
    return correct.count(True)/len(correct)

def train_loss(parameters):
    loss_accu = 0
    for img_i in range(train_num):
        loss_accu+=sqr_loss(train_img[img_i],train_lab[img_i],parameters)
    return loss_accu/(train_num/10000)
def train_accuracy(parameters):
    correct = [predict(train_img[img_i],parameters).argmax()==train_lab[img_i] for img_i in range(train_num) ]
    return correct.count(True)/len(correct)

解释一下在计算误差的时候为什么要再除以10000。这个就是为了后面数据显示的好看，表示数据集中每10000个数据的平均误差

2. 初始化，准备收集数据

将误差和精确度放在list里面

parameters=init_parameters()#初始化参数
current_epoch=0#当前的时期
train_loss_list=[]#训练集的误差
valid_loss_list=[]#验证集的误差
train_accu_list=[]#训练集的精确度
valid_accu_list=[]#验证集的精确度

解释一下这个epoch。epoch是中文意思就是时期。在神经网络里面就是当一个完整的数据集通过了神经网络一次并且返回了一次，这个过程称为一次epoch。而我们需要多个epoch,因为在神经网络中传递完整的数据集一次是不够的，而且我们需要将完整的数据集在同样的神经网络中传递多次。但请记住，我们使用的是有限的数据集，并且我们使用一个迭代过程即梯度下降来优化学习过程。

3. 进行训练

这里的学习率还是一开始的1。训练完一次后,epoch加1，并且将训练集和验证集的误差与精确度放入对应的list当中保存。

from tqdm import tqdm
learn_rate=1#学习率
epoch_num=10#时期数，也就是训练多少次
for epoch_num in tqdm(range(epoch_num)):
    for i in range(train_num//batch_size):
        gard_tmp=train_batch(i,parameters)
        parameters=combine_parameters(parameters,gard_tmp,learn_rate)
    current_epoch+=1
    train_loss_list.append(train_loss(parameters))
    train_accu_list.append(train_accuracy(parameters))
    valid_loss_list.append(valid_loss(parameters))
    valid_accu_list.append(valid_accuracy(parameters))

解释一下这个tqdm。Tqdm 是一个快速，可扩展的Python进度条，可以在 Python 长循环中添加一个进度提示信息，用户只需要封装任意的迭代器 tqdm(iterator)。如图所示：

有了进度条就不用跟上个博客中一样，用print的方法来表示进度了。至于进度的快慢取决于电脑CPU的频率，多线程运行。

4. 作出图表

通过图表的方式来反应误差和精确度，方便分析。
代码如下所示：

#误差
lower=0
#[a:b]表示的列表中的范围，从a到b。下面的代码中则表示从第0个开始
plt.plot(valid_loss_list[lower:],color='black',label='validation loss')
plt.plot(train_loss_list[lower:],color='red',label='train loss')

结果如下：

#精确度
plt.plot(valid_accu_list[lower:],color='black',label='validation loss')
plt.plot(train_accu_list[lower:],color='red',label='train loss')
plt.show

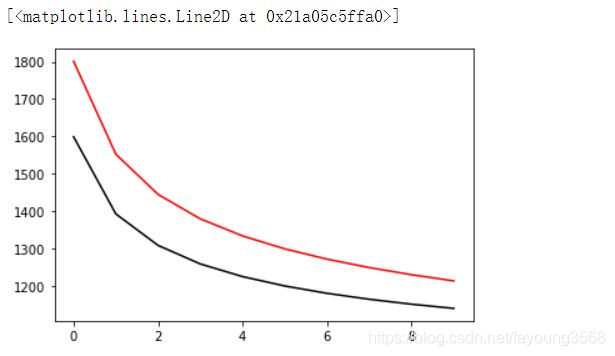
结果如下：

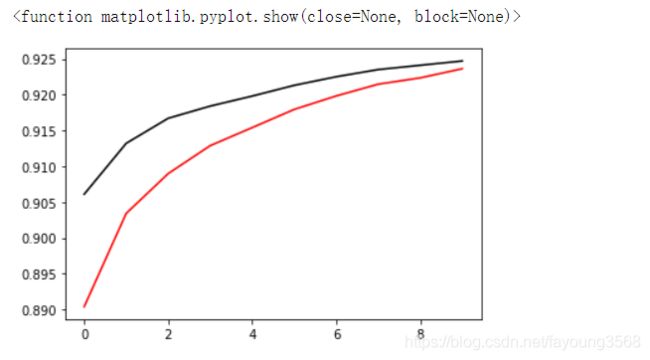
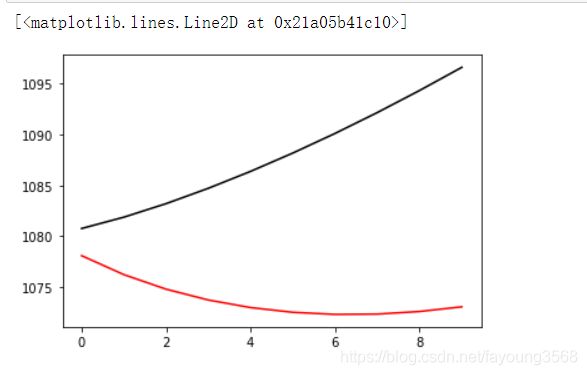
由此可见，我们第一次训练的结果还是好的，误差在逐渐的减小，精确度再逐渐的上升。

注意到，黑线是验证集，红线是训练集。从图表上我们可以看出验证集的训练效果是比训练集的训练效果好的。结合之前博客中提到的数据集的类比，就是你平常上课不好好听讲，但是课后练习还是做的比较好。这是一个有意思的现象，应该是训练次数太少或者数据集太少的原因导致的。

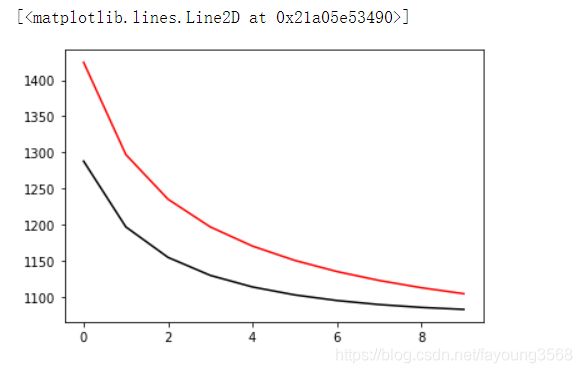
5. 再训练一次

误差结果如下：

误差还在继续减小
精确度结果如下：

精确度还在提升，但是我们注意到红线已经赶上黑线了，但是二者都有趋平的态势。也就是说在这次训练中，以学习率为1进行梯度下降，误差和精确度的变化在逐渐减小，也就是要到最低点了。

6. 再训练一次看看
   误差结果如下：
   
   误差还在继续减小
   精确度结果如下：
   
   这时红线已经超过黑线了。

说明还没有到最低点，这个学习率还是可以的。接下来对学习率进行分析

7. 调整学习率

取一个随机训练组，将训练组中的参数梯度赋给学习率的梯度，即grad_lr。然后通过学习率和误差的关系来反应学习率的好坏。
代码如下：

rand_batch=np.random.randint(train_num//batch_size)
grad_lr=train_batch(rand_batch,parameters)

lr_list=[]#将学习率放入list中保存
lower=-5#下界
upper=2#上界
step=1#步长
#以step为单位，把区间[lower,upper]划分为num个数字
for lr_pow in tqdm(np.linspace(lower,upper,num=(upper-lower)//step+1)):
	#对学习率进行等比缩放，比等差缩放会快一点，下面代码则以10的多少次方比进行缩放
    learn_rate=10**lr_pow
    parameters_tmp=combine_parameters(parameters,grad_lr,learn_rate)
    train_loss_tmp=train_loss(parameters_tmp)
    lr_list.append([lr_pow,train_loss_tmp])

numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
在指定的间隔内返回均匀间隔的数字。
返回num均匀分布的样本，在[start, stop]。
这个区间的端点可以任意的被排除在外。
如图所示：

lr_list如下：

8. 作出学习率的图表

代码如下：

plt.plot(np.array(lr_list)[:,0],np.array(lr_list)[:,1],color='black')
plt.show

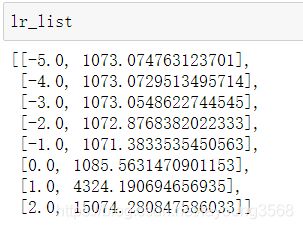
结果如下所示：

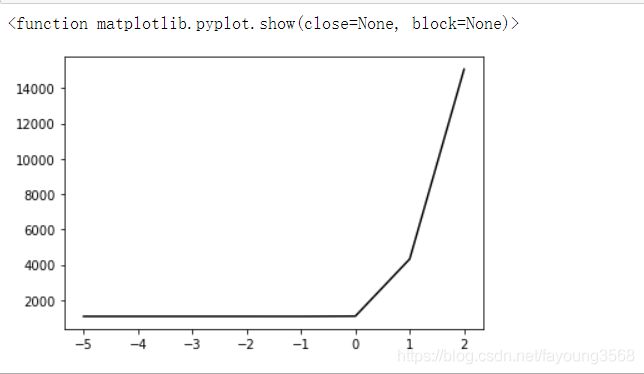
由于误差的范围太大了，不能确定最低点在哪里。虽然看上去是0出最低，我们把[0,2]这个区间去掉看看。
代码如下：

#[:-2]表示从上界到倒数第二个。第0列为x轴，第1列为y轴
plt.plot(np.array(lr_list)[:-2,0],np.array(lr_list)[:-2,1],color='black')
plt.show

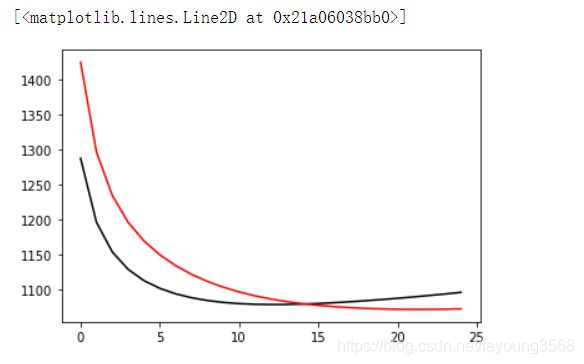
结果如图所示：

这就很明显了，在-1左右是最低点。根据这个图标我们可以把upper确定为0，lower确定为-2。在这个区间内进行学习率进行进一步判断。

9. 调整代码

调整后代码如下：

lr_list=[]
lower=-2
upper=0
step=0.1
#因为step是浮点数，除了之后还是浮点数，所以num要用int()强制转换一下。
for lr_pow in tqdm(np.linspace(lower,upper,num=int((upper-lower)//step+1))):
    learn_rate=10**lr_pow
    parameters_tmp=combine_parameters(parameters,grad_lr,learn_rate)
    train_loss_tmp=train_loss(parameters_tmp)
    lr_list.append([lr_pow,train_loss_tmp])
    
upper=len(lr_list)
plt.plot(np.array(lr_list)[:upper,0],np.array(lr_list)[:upper,1],color='black')
plt.show

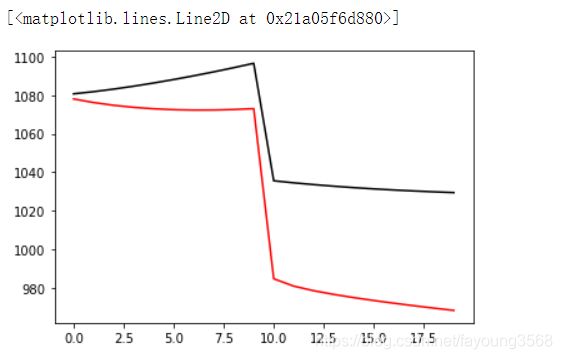
结果如下：

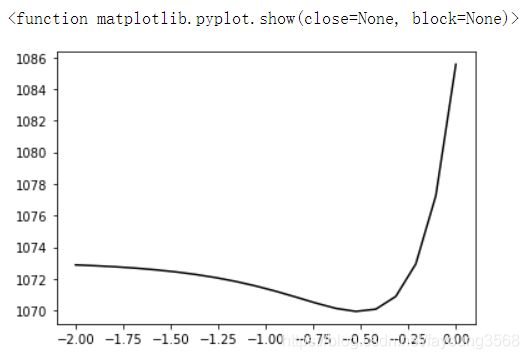
由此，我们可以看出在-0.6到-0.3之间是有最低点的。这里我们取学习率为-0.6。

10. 在学习率调整之前在训练一次
    代码如下：

learn_rate=1
epoch_num=10
for epoch_num in tqdm(range(epoch_num)):
    for i in range(train_num//batch_size):
        gard_tmp=train_batch(i,parameters)
        parameters=combine_parameters(parameters,gard_tmp,learn_rate)
    current_epoch+=1
    train_loss_list.append(train_loss(parameters))
    train_accu_list.append(train_accuracy(parameters))
    valid_loss_list.append(valid_loss(parameters))
    valid_accu_list.append(valid_accuracy(parameters))

lower=0
plt.plot(valid_loss_list[lower:],color='black',label='validation loss')
plt.plot(train_loss_list[lower:],color='red',label='train loss')

结果如下：

误差开始上升，这就说明过了最低点，又往上走了。

plt.plot(valid_accu_list[lower:],color='black',label='validation loss')
plt.plot(train_accu_list[lower:],color='red',label='train loss')
plt.show

结果如下：

同样说明过了最低点了。

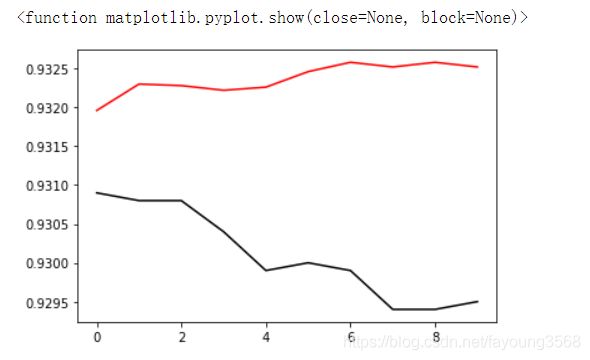
为了看的更清楚，取最后10个看一下。代码如下：

lower=-10
plt.plot(valid_loss_list[lower:],color='black',label='validation loss')
plt.plot(train_loss_list[lower:],color='red',label='train loss')

结果如下：

plt.plot(valid_accu_list[lower:],color='black',label='validation loss')
plt.plot(train_accu_list[lower:],color='red',label='train loss')
plt.show

结果如下：

发现都过了最低点，都在左右横跳。

11. 调整学习率后进行训练

代码如下：

learn_rate=10**-0.6
epoch_num=10
for epoch_num in tqdm(range(epoch_num)):
    for i in range(train_num//batch_size):
        gard_tmp=train_batch(i,parameters)
        parameters=combine_parameters(parameters,gard_tmp,learn_rate)
    current_epoch+=1
    train_loss_list.append(train_loss(parameters))
    train_accu_list.append(train_accuracy(parameters))
    valid_loss_list.append(valid_loss(parameters))
    valid_accu_list.append(valid_accuracy(parameters))

lower=-20
plt.plot(valid_loss_list[lower:],color='black',label='validation loss')
plt.plot(train_loss_list[lower:],color='red',label='train loss')

结果如下：

plt.plot(valid_accu_list[lower:],color='black',label='validation loss')
plt.plot(train_accu_list[lower:],color='red',label='train loss')
plt.show

结果如下：

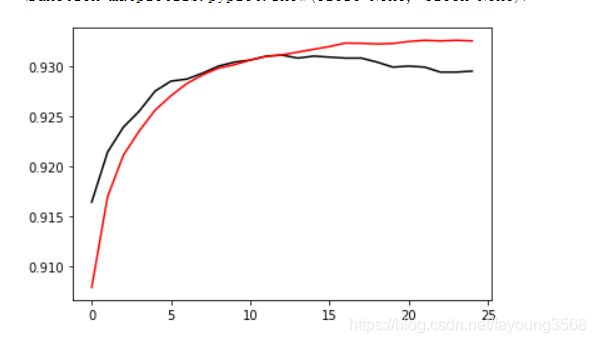
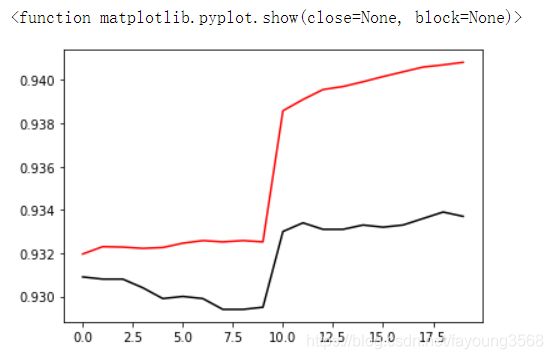
由此，我们可以看出在学习率取10**-0.6时，误差的下降和精确度的上升是训练中幅度最大的，训练后期的变化趋势也是趋于平缓。但是我们也可以看出出现了一点过拟合现象，即训练集和验证集的结果相差过大。

代码解释

#定义数据集的误差和精确度
def valid_loss(parameters):
    loss_accu = 0
    for img_i in range(valid_num):
        loss_accu+=sqr_loss(valid_img[img_i],valid_lab[img_i],parameters)
    return loss_accu/(valid_num/10000)
def valid_accuracy(parameters):
    correct = [predict(valid_img[img_i],parameters).argmax()==valid_lab[img_i] for img_i in range(valid_num) ]
    return correct.count(True)/len(correct)

def train_loss(parameters):
    loss_accu = 0
    for img_i in range(train_num):
        loss_accu+=sqr_loss(train_img[img_i],train_lab[img_i],parameters)
    return loss_accu/(train_num/10000)
def train_accuracy(parameters):
    correct = [predict(train_img[img_i],parameters).argmax()==train_lab[img_i] for img_i in range(train_num) ]
    return correct.count(True)/len(correct)

#初始化，准备收集数据
parameters=init_parameters()
current_epoch=0
train_loss_list=[]
valid_loss_list=[]
train_accu_list=[]
valid_accu_list=[]

#进行训练
from tqdm import tqdm
learn_rate=10**-0.6
epoch_num=10
for epoch_num in tqdm(range(epoch_num)):
    for i in range(train_num//batch_size):
        gard_tmp=train_batch(i,parameters)
        parameters=combine_parameters(parameters,gard_tmp,learn_rate)
    current_epoch+=1
    train_loss_list.append(train_loss(parameters))
    train_accu_list.append(train_accuracy(parameters))
    valid_loss_list.append(valid_loss(parameters))
    valid_accu_list.append(valid_accuracy(parameters))
    
#作出图表

#误差
lower=-20
plt.plot(valid_loss_list[lower:],color='black',label='validation loss')
plt.plot(train_loss_list[lower:],color='red',label='train loss')

#精确度
plt.plot(valid_accu_list[lower:],color='black',label='validation loss')
plt.plot(train_accu_list[lower:],color='red',label='train loss')
plt.show

#调整学习率
rand_batch=np.random.randint(train_num//batch_size)
grad_lr=train_batch(rand_batch,parameters)

lr_list=[]
lower=-2.75
upper=-0.25
step=0.25
num_tmp=(upper-lower)//step+1
for lr_pow in tqdm(np.linspace(lower,upper,num=int((upper-lower)//step+1))):
    learn_rate=10**lr_pow
    parameters_tmp=combine_parameters(parameters,grad_lr,learn_rate)
    train_loss_tmp=train_loss(parameters_tmp)
    lr_list.append([lr_pow,train_loss_tmp])
#作出学习率和误差的图表
upper=len(lr_list)
plt.plot(np.array(lr_list)[:upper,0],np.array(lr_list)[:upper,1],color='black')
plt.show

每日一句：你若盛开，蝴蝶自来。