算法实现(JAVA)
目录
前言
第一章 概述
一、算法复杂度
二、汉诺塔问题
三、判断素数
四、判断回文
第二章 递归算法设计技术
一、递归
二、二叉树
三、复制二叉树
四、二叉树节点之和
五、N皇后问题
六、递归求字符个数
七、非递归二叉树
第三章 分治法
一、快速排序
二、查找最大和次大元素
三、寻找中位数所在的位置
四、折半查找
五、查找第k小元素
六、寻找两个等长有序序列的中位数
七、归并排序
八、折半查找的拓展
九、最大序列和(分治法)
第四章 蛮力法
一、找数字
二、完美数
三、数列分段
四、最大子序列和(蛮力法)--3种实现方法
五、 最小差值
六、相邻数对
七、报数游戏
八、简单选择排序
九、冒泡排序
前言
本文是用来记录在大三下学期学习《算法设计与分析》这门课时,根据老师布置的作业,用java实现的算法代码。本文仅供学习交流使用,侵删。
第一章 概述
一、算法复杂度
计算复杂度主要是找到程序的运行关系
详细的内容可见该博客一文讲透算法中的时间复杂度和空间复杂度![]() https://www.cnblogs.com/lonely-wolf/p/15674526.html
https://www.cnblogs.com/lonely-wolf/p/15674526.html
二、汉诺塔问题
1、描述
2、实现代码
public class HanioTest {
public static void main(String[] args) throws IOException {
System.out.println("请输入盘子数:");
Scanner scanner = new Scanner(System.in);
int i = scanner.nextInt();
hanio(i,'a','b','c');
}
public static void hanio(int n ,char a,char b,char c) throws IOException {
/**
* @description: 用递归的方式解决汉诺塔问题
* @param n 多少个盘子
* @param a 第一个柱子a
* @param b 第一个柱子b
* @param c 第一个柱子c
* @return: void
* @author: fayoung
* @time: 2022/3/3 17:27
*/
if (n == 1){
move(n,a,c);
}else {
hanio(n-1,a,c,b);
move(n,a,c);
hanio(n-1,b,a,c);
}
}
public static void move(int n,char a,char b) throws IOException {
/**
*
*
* @description:
* @param n 第几个盘子
* @param a 要移动的盘子的起始位子
* @param b 要移动的盘子的放置位置
* @return: void
* @author: fayoung
* @time: 2022/3/3 17:29
*/
File file = new File("src/com/fayoung/ach/date2_28/hanio/output.txt");
if (file.exists()){
file.createNewFile();
}
FileWriter fw = new FileWriter("src/com/fayoung/ach/date2_28/hanio/output.txt", true);
PrintWriter pw = new PrintWriter(fw);
pw.println("把第"+n+"个盘子从"+a+"移到"+b);
pw.flush();
}
}3、结果
4、时间复杂度
设盘子个数为n时,需要T(n)步,把A柱子n-1个盘子移到B柱子,需要T(n-1)步,A柱子最后一个盘子移到C柱子一步,B柱子上n-1个盘子移到C柱子上T(n-1)步。
得递推公式T(n)=2T(n-1)+1
所以汉诺塔问题的时间复杂度为O(2^n);
三、判断素数
1、描述
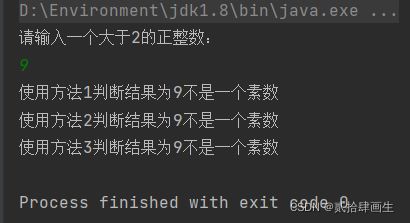
判断一个大于2的正整数n是否为素数的方法有很多中,给出两种算法,说明其中哪种算法更好的理由。
2、实现代码
public class isPrimeNumber {
public static void main(String[] args) {
System.out.println("请输入一个大于2的正整数:");
Scanner scanner1 = new Scanner(System.in);
int x = scanner1.nextInt();
if (isPrimeNumber.way1(x))
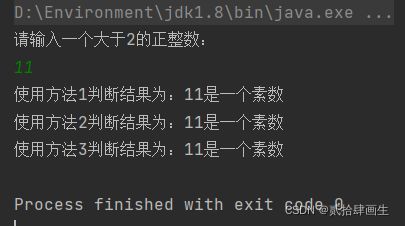
System.out.println("使用方法1判断结果为:" + x + "是一个素数");
else
System.out.println("使用方法1判断结果为" + x + "不是一个素数");
if (isPrimeNumber.way2(x))
System.out.println("使用方法2判断结果为:" + x + "是一个素数");
else
System.out.println("使用方法2判断结果为" + x + "不是一个素数");
if (isPrimeNumber.way3(x,2))
System.out.println("使用方法3判断结果为:" + x + "是一个素数");
else
System.out.println("使用方法3判断结果为" + x + "不是一个素数");
}
//将n与[1,n-1]相取余,判断是否为0。如果为0则表示可以整除,该数就部署素数。反之就是素数
public static boolean way1(int n) {
Boolean flag = true;
for (int i = 2; i < n; i++) {
if (n % i == 0) {
flag = false;
break;
} else
flag = true;
}
return flag;
}
//将n与[1,根号n]相取余,判断是否为0。如果为0则表示可以整除,该数就部署素数。反之就是素数
public static boolean way2(int n) {
Boolean flag = true;
for (int i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
flag = false;
break;
} else
flag = true;
}
return flag;
}
//用递归的方式处理,终止条件为取余为0
public static boolean way3(int n ,int i){
if(i==n) return true;
if (n%i==0) return false;
return way3(n,++i);
}
}
3、结果
4、时间复杂度
方法一为O(n);方法二为O(根号n);方法三为O(n)
四、判断回文
1、描述
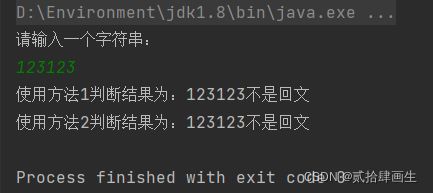
一个字符串采用string对象存储,设计一个算法判断该字符串是否为回文。
2、实现代码
public class isPalinDrome {
public static void main(String[] args) {
System.out.println("请输入一个字符串:");
Scanner scanner = new Scanner(System.in);
String s = scanner.next();
if (fun1(s))
System.out.println("使用方法1判断结果为:" + s + "是回文");
else
System.out.println("使用方法1判断结果为:" + s + "不是回文");
if (fun2(s,0,s.length()))
System.out.println("使用方法2判断结果为:" + s + "是回文");
else
System.out.println("使用方法2判断结果为:" + s + "不是回文");
}
//将该字符串先转成字符数组s1,然后复制该该字符数组s2。将s2和s1反向对比,判断回文
public static boolean fun1(String s) {
Boolean flag = true;
char[] s1 = s.toCharArray();
char[] s2 = new char[s1.length];
int n=s1.length;
for (int i = 0; i 3、结果
4、时间复杂度
方法一:O(n);方法二:O(n);
第二章 递归算法设计技术
一、递归
1、描述
递归(英语:recursion)在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。
2、总结
递归是将站在全局,将大问题转化成小问题,主要是要找到递归关系式。
二、二叉树
1、描述
基础知识可见此博客数据结构与算法——二叉树基础![]() https://xiaozhuanlan.com/topic/7189032546
https://xiaozhuanlan.com/topic/7189032546
2、实现二叉树
treeNode
//用类去实现数据结构
public class TreeNode {
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode(char x){
val =x;
}
}TreeNodeUtil
public class TreeNodeUtil {
public static TreeNode arrayToTreeNode(char[] array){
if(array.length == 0){
return null;
}
TreeNode root = new TreeNode(array[0]);
Queue queue = new LinkedList();
queue.add(root);
boolean isLeft = true;
for(int i = 1; i < array.length; i++){
TreeNode node = queue.peek();
if(isLeft){
if(array[i] != '0'){
node.left = new TreeNode(array[i]);
queue.offer(node.left);
}
isLeft = false;
}else {
if(array[i] != '0'){
node.right = new TreeNode(array[i]);
queue.offer(node.right);
}
queue.poll();
isLeft = true;
}
}
return root;
}
} TreeNodeShow
public class TreeNodeShow {
private static int getTreeDepth(TreeNode root){
return root == null ? 0 : (1+ Math.max(getTreeDepth((root.left)), getTreeDepth(root.right)));
}
private static void writeArray(TreeNode currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
// 保证输入的树不为空
if (currNode == null) return;
// 先将当前节点保存到二维数组中
res[rowIndex][columnIndex] = String.valueOf(currNode.val);
// 计算当前位于树的第几层
int currLevel = ((rowIndex + 1) / 2);
// 若到了最后一层,则返回
if (currLevel == treeDepth) return;
// 计算当前行到下一行,每个元素之间的间隔(下一行的列索引与当前元素的列索引之间的间隔)
int gap = treeDepth - currLevel - 1;
// 对左儿子进行判断,若有左儿子,则记录相应的"/"与左儿子的值
if (currNode.left != null) {
res[rowIndex + 1][columnIndex - gap] = "/";
writeArray(currNode.left, rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
}
// 对右儿子进行判断,若有右儿子,则记录相应的"\"与右儿子的值
if (currNode.right != null) {
res[rowIndex + 1][columnIndex + gap] = "\\";
writeArray(currNode.right, rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
}
}
public static void show(TreeNode root) {
if (root == null){
System.out.println("EMPTY!");
return;
}
// 得到树的深度
int treeDepth = getTreeDepth(root);
// 最后一行的宽度为2的(n - 1)次方乘3,再加1
// 作为整个二维数组的宽度
int arrayHeight = treeDepth * 2 - 1;
int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
// 用一个字符串数组来存储每个位置应显示的元素
String[][] res = new String[arrayHeight][arrayWidth];
// 对数组进行初始化,默认为一个空格
for (int i = 0; i < arrayHeight; i++) {
for (int j = 0; j < arrayWidth; j++) {
res[i][j] = " ";
}
}
// 从根节点开始,递归处理整个树
// res[0][(arrayWidth + 1)/ 2] = (char)(root.val + '0');
writeArray(root, 0, arrayWidth / 2, res, treeDepth);
// 此时,已经将所有需要显示的元素储存到了二维数组中,将其拼接并打印即可
for (String[] line : res) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < line.length; i++) {
sb.append(line[i]);
if (line[i].length() > 1 && i <= line.length - 1) {
i += line[i].length() > 4 ? 2 : line[i].length() - 1;
}
}
System.out.println(sb.toString());
}
}
}test
public class Test {
public static void main(String[] args) {
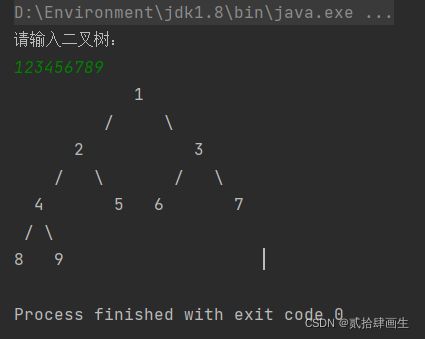
System.out.println("请输入二叉树:");
Scanner scanner = new Scanner(System.in);
String s = scanner.next();
char[] s1 = s.toCharArray();
TreeNode q = TreeNodeUtil.arrayToTreeNode(s1);
TreeNodeShow.show(q);
}
}3、结果
三、复制二叉树
1、描述
给定一个二叉树,复制该二叉树
2、代码实现
/**
* @description:复制二叉树
* @author: fayoung
* @time: 2022/3/9 10:20
*/
class TreeNode{
int val=0;
TreeNode left;
TreeNode right;
public int getVal() {
return val;
}
public void setVal(int val) {
this.val = val;
}
public TreeNode getLeft() {
return left;
}
public void setLeft(TreeNode left) {
this.left = left;
}
public TreeNode getRight() {
return right;
}
public void setRight(TreeNode right) {
this.right = right;
}
}
public class CopyBT {
public TreeNode copyTree(TreeNode root){
TreeNode copyRoot = new TreeNode();
if (root!=null){
copyRoot.setVal(root.getVal());
copyRoot.setLeft(root.getLeft());
copyRoot.setRight(root.getRight());
}
return copyRoot;
}
public static void main(String[] args) {
TreeNode root = new TreeNode();
TreeNode left = new TreeNode();
TreeNode right = new TreeNode();
TreeNode node = new TreeNode();
root.setVal(1);
right.setVal(2);
left.setVal(3);
node.setVal(4);
root.setRight(right);
root.setLeft(left);
root.getLeft().setLeft(node);
TreeNode copy1 = new CopyBT().copyTree(root);
System.out.println("原来的树:"+ root.getVal()+" "+left.getVal()+" "+right.getVal()+" "+left.left.getVal());
System.out.println("复制后的树:"+copy1.getVal()+" "+copy1.getLeft().getVal()+" "+copy1.getRight().getVal()+
" "+copy1.getLeft().getLeft().getVal());
}
}
3、结果
四、二叉树节点之和
1、描述
给定一个字节类型为Int的二叉树,计算该二叉树各节点之和。
2、代码实现
/**
* @description:二叉树节点之和
* @author: fayoung
* @time: 2022/3/9 10:59
*/
public class SumBTNode {
public static void main(String[] args) {
BTNode root = new BTNode();
BTNode right = new BTNode();
BTNode left = new BTNode();
root.setVal(1);
right.setVal(5);
left.setVal(3);
root.setRight(right);
root.setLeft(left);
int sumBTNode = new SumBTNode().Sum(root);
System.out.println("二叉树:"+root.getVal()+" "+left.getVal()+" "+right.getVal());
System.out.println("节点之和为:"+sumBTNode);
}
public int Sum(BTNode root) {
if (root != null)
return root.getVal() + Sum(root.getLeft()) + Sum(root.getRight());
return 0;
}
}
class BTNode{
int val;
BTNode left;
BTNode Right;
public int getVal() {
return val;
}
public void setVal(int val) {
this.val = val;
}
public BTNode getLeft() {
return left;
}
public void setLeft(BTNode left) {
this.left = left;
}
public BTNode getRight() {
return Right;
}
public void setRight(BTNode right) {
Right = right;
}
}3、结果
五、N皇后问题
1、描述
N皇后问题是将n个皇后放置在n*n的棋盘上,皇后彼此之间不能相互攻击(任意两个皇后不能位于同一行,同一列,同一斜线)。给定一个整数n,返回所有不同的N皇后问题的解决方案。
2、代码实现
/**
* @description:用递归解决n皇后问题
* @author: fayoung
* @time: 2022/3/9 16:55
*/
public class NQueen {
static int max=4;//有几个皇后
int[] array=new int[max];//用一维数组表示皇后所在的位置,值表示所在列,下标表示所在行
static int count=0;//解法的个数
public static void main(String[] args) {
NQueen q = new NQueen();
q.check(0);
System.out.println( max+"皇后问题的解法有" + count + "种");
}
private boolean judge( int n){ //判断放入第n个皇后是否冲突
for (int i = 0; i < n; i++) {
if (array[n] == array[i] || Math.abs(n - i) == Math.abs(array[n] - array[i])) { //在同一列或者同一斜线
return false; //冲突
}
}
return true;
}
public void check ( int n){ //递归调用check
if (n == max) {
print();
count++;
return;
}
for (int i = 0; i < max; i++) {
array[n] = i;
if (judge(n)) {
check(n + 1);
}
}
}
private void print() { //打印n皇后的一种解法
for (int i = 0; i < max; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
}3、结果
六、递归求字符个数
1、描述
对于一个采用字符数组存放的字符串str,设计一个递归算法求其字符个数(长度)
2、实现代码
/**
* @description:对于一个采用字符数组存放的字符串str,设计一个递归算法求其字符个数(长度)
* @author: fayoung
* @time: 2022/3/9 21:20
*/
public class CharLength {
public int length(String str,int i){
if (str ==null){
return 0;
}
if(i>= str.length())
return 0;
else {
return 1+length(str,++i);
}
}
public static void main(String[] args) {
String s = "hello world";
int length = new CharLength().length(s,0);
System.out.println(s+"的字符长度为:"+length);
}
}3、结果
七、非递归二叉树
1、描述
假设二叉树采用二叉链存储结构存放,节点值为Int类型,设计一个非递归算法求二叉树bt中所有叶子节点值大于等于k的节点个数。
2、代码实现
/**
* @description:二叉树二叉链表的java实现。假设二叉树采用二叉链存储结构存放,节点类型为int类型,设计一个非递归算法求二叉数bt中所有节点值大于等于k的节点的个数
* @author: fayoung
* @time: 2022/3/10 8:44
*/
public class BinaryChainTree {
public static void main(String[] args) {
BinaryChainTree tree = new BinaryChainTree();
Node node = new Node();
node=tree.creat(1);
tree.add(node,2,true );
tree.add(node,3,false);
int k =2;
System.out.println("二叉树:"+" "+tree.root.data+" "+tree.root.left.data+" "+tree.root.right.data);
System.out.println("该二叉树中大于等于"+k+"的节点个数为:"+num(tree, k));
}
//二叉链树的节点,也就是域,每个节点都有三个域,分别为左、根、右
public static class Node{
Integer data;//用Inter类型是因为int无法判空
Node left;
Node right;
//无参构造,以可以new出来
public Node(){
}
//有参构造
public Node(int data){
this.data=data;
this.left=null;
this.right=null;
}
}
private Node root;
//根据提供的元素构造二叉树
public Node creat(Integer data){
return root = new Node(data);
}
//为指定节点添加子节点
public Node add(Node parent,int data,boolean isLeft){
//如果提供的节点为空,则不能添加子节点
if(parent==null||parent.data==null){
throw new RuntimeException("节点为空的不能添加子节点");
}
Node node=null;
if(isLeft){//如果要添加的是左子节点
if(parent.left!=null){
throw new RuntimeException("该节点的左子节点已经存在");
}else{
node=new Node(data);
parent.left=node;
}
}else{//否则添加的是右子节点
if(parent.right!=null){
throw new RuntimeException("该节点的右子节点已经存在");
}else{
node=new Node(data);
parent.right=node;
}
}
return node;
}
//采用非递归的方法进行遍历,统计大于k的节点的个数
public static int num(BinaryChainTree tree,int k) {
int num=0;//大于k的节点的个数
Stack stack = new Stack();
if (tree == null){//树为空,返回0
return 0;
}
stack.push(tree.root);//将树的根节点入栈
while (!stack.isEmpty()){//当栈不为空时
Node pop = stack.pop();//用一个变量Node表示出栈的根节点
if (pop!=null){//如果根节点不为空
if (pop.data>=k){//如果根节点的值大于k,则num++
num++;
}
stack.push(pop.right);//将根的右节点入栈
stack.push(pop.left);//将根的左节点入栈
}
}
return num;//返回个数
}
} 3、结果
第三章 分治法
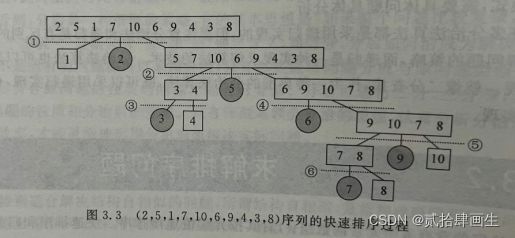
一、快速排序
1、描述
快速排序的基本思想是在待排序的n个元素中任取一个元素(通常取第一个元素)作为基准,把该元素放人最终位置后,整个数据序列被基准分割成两个子序列,所有小于基准的元素放置在前子序列中,所有大于基准的元素放置在后子序列中,并把基准排在这两个子序列的中间,这个过程称为
划分。然后对两个子序列分别重复上述过程,直到每个子序列内只有一个元素或空为止。
2、代码实现
package com.fayoung.ach.date3_14;
import java.util.Arrays;
/**
* @description:快速排序(分治法)
* 实现步骤:
* 1、从数列中挑出一个元素,称为 "基准"(pivot),一般是数组开头的第一个
* 2、重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
* 所以实际上我们需要找到中间的某个位置 k,这样 k 左边的值全部比 k 上的值小,k 右边的值全部比 k 上的值大。然而分区算法有很多中,这里选择哨兵分区,也叫做两边交换法
* ①右边的哨兵guardR先从数列最后一个开始由右往左找一个小于基准的数,左边的哨兵guardL再从数列第二个开始由左往右找一个大于基准的数,然后把右边比基准小的放在左边,左边比基准大的放在右边,与基准相同的在原地。
* ②完成后,右边的哨兵guardR继续从右往左找一个小于基准的数,左边的哨兵guardL继续从左往右找一个大于基准的数,进行交换。直到guardL==guardR,即哨兵相遇。
* ③将基准再放到此时哨兵所在的位置,基准就到了数列中间,左边是比基准小的数,右边是比基准大的数
* 3、递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;也就是把各个分区进行相同操作,直到分区里只有一个元素。
* @author: fayoung
* @time: 2022/3/14 19:36
*/
public class QuicklySort {
public static int Partition(int[] a,int s,int f){//分区,返回分区之间的位置,也就是从数列哪里进行划分
int guardR=f; //右边的哨兵
int guardL=s; //左边的哨兵
int pivot = a[s];//基准:数列第一个
if (guardLguardL){
while (guardR>guardL && a[guardR]>=pivot)//哨兵i从右向左找比基准值小的数值
guardR--;
a[guardL] = a[guardR];//此时右边的哨兵所在位置的值是小于基准的,将这个值放在左边
while (guardL 3、结果
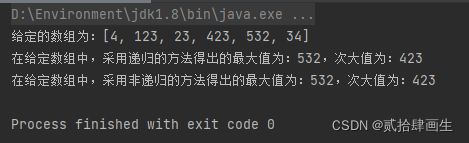
二、查找最大和次大元素
1、描述
对于给定的含有n个元素的无序序列,用递归和非递归的方式,求出这个序列中最大和次大的元素。
2、代码实现
/**
* @description:查找最大和次大元素,用递归和非递归的方式实现。递归就是用分治的思想,非递归就是用遍历的思想
* @author: fayoung
* @time: 2022/3/15 19:55
*/
public class FindFirstAndSecond {
public static void main(String[] args) {
int[] a = {4,123,23,423,532,34};
FASMax fasMax = divideAndConquer(a, 0, a.length - 1);
FASMax traversal = traversal(a);
System.out.println("给定的数组为:"+ Arrays.toString(a));
System.out.println("在给定数组中,"+"采用递归的方法得出的"+"最大值为:"+fasMax.max1+",次大值为:"+fasMax.max2);
System.out.println("在给定数组中,"+"采用非递归的方法得出的"+"最大值为:"+traversal.max1+",次大值为:"+traversal.max2);
}
/**
* first and second max自定义的类,用于存放最大值和次大值
*/
static class FASMax{
int max1;//最大值
int max2;//次大值
public FASMax() {//无参构造
}
}
/**
* 分治法求解分析:
*先给出无序序列数组a[...]。
* 1、第一种情况为当数组中只有一个元素时,此时只存在一个最大值即为本身,次大值为负无穷;
* 2、第二种情况为数组中只有两个元素,此时最大值和次大值很显然将两个元素比较即可;
* 3、第三种情况为数组中的元素大于两个,此时用分治法,将数组中元素砍为两半,注意的是此时中间的点归为前半部分;
* 4、接着我们对前半部分再次进行判断三种情况,再对后半部分做同样的操作,因为我们每次判断返回的都是当前判断的一部分的最大值和次大值;
* 5、因此折半后两边都有最大值和次大值,再将两边的四个值比较找出最大值和次大值;
* @param a :所要查找的数组
* @param s:数组的第一下标
* @param f :数组最后一个下标
* @return 返回数组a中的最大值和次大值
*/
public static FASMax divideAndConquer(int[] a,int s,int f){//分治的方式
FASMax divideAndConquer = new FASMax();
if (s==f){//如果数组只有一个元素
divideAndConquer.max1=a[s];//最大值就为该元素
divideAndConquer.max2=Integer.MIN_VALUE;//次大的值为-∞,在这里用Integer.MIN_VALUE表示
}else if (s==f-1){//如果数组有两个元素
divideAndConquer.max1=Math.max(a[s],a[f]);//最大值为两个元素中最大的一个
divideAndConquer.max2=Math.min(a[s],a[f]);//次大值为两个元素中最小的一个
}else {//如果数组大于两个元素
int mid=(s+f)/2;//得到数组的中间下标
FASMax front = divideAndConquer(a,s,mid);//front为数组a前半部分的最大值和次大值(包括a[mid])
FASMax last = divideAndConquer(a,mid+1,f);//last为数组a后半部分的最大值和次大值
if(front.max1>last.max1){//如果前半部分的最大值大于后半部分的最大值
divideAndConquer.max1=front.max1;//最大值为前半部分的最大值
divideAndConquer.max2=Math.max(front.max2,last.max1);//次大值为前半部分的次大值和后半部分最大中最大的一个
}else {//如果前半部分的最大值小于后半部分的最大值
divideAndConquer.max1=last.max1;//最大值为后半部分的最大值
divideAndConquer.max2=Math.max(last.max2, front.max1);//次大值为后半部分的次大值和前半部分的最大值中最大的一个
}
}
return divideAndConquer;//将最大值和次大值返回
}
/**
* 该方法采用对数组遍历的方式,找出最大值和次大值
* 1、最大值和次大值都从数组第一个元素开始找
* 2、如果如果此时的最大值小于当前元素的值,找最大值
* 3、如果此时的最大值大于当前元素的值,找次大值
* @param a:所要查找的数组
* @return 返回数组a中的最大值和次大值
* */
public static FASMax traversal(int[] a){
FASMax traversal = new FASMax();
先初始化,最大值为数组第一个,次小值也为数组第一个
traversal.max1=a[0];
traversal.max2=a[0];
for (int i = 0; i 3、结果
三、寻找中位数所在的位置
1、描述
已知由n(n>=2)个正整数构成的集合A ,将其划分成两个不相交的子集A1和A2,元素个数分别为n1和n2,A1和A2中元素之和分别为S1和S2。设计一个尽可能高效的划分算法,满足|n1-n2|最小且|S1-S2|最大。 要求: 1)给出算法的基本设计思想。 2)根据设计思想,采用C或C++语言描述算法,关键之处给出注释。 3)说明你所设计算法的平均时间复杂度和空间复杂度。
2、代码实现
/**
* @description:已知由n(n>=2)个正整数构成的集合A ,将其划分成两个不相交的子集A1和A2,元素个数分别为n1和n2,A1和A2中元素之和分别为S1和S2。设计一个尽可能高效的划分算法,满足|n1-n2|最小且|S1-S2|最大。
* @author: fayoung
* @time: 2022/3/15 21:46
*/
import java.util.ArrayList;
import java.util.Arrays;
/**
*思路:求解该问题的思路为要|n1-n2|最小且|S1-S2|最大,那两个小集合的元素数量就要尽可能相同,一个小集合放集合A中较小的数,另一个小集合放集合A中较大的数,这就想到了快速排序中的分区。也就是用分治的思想解决这个问题
* 也就是要找到划分分区的那个位置position.
* 1、如果position=n/2,则结束,找到了那个位置
* 2、如果positionn/2,那position后面所有的元素都属于A2,继续对position之前的元素进行划分
*/
public class FundPosition {
public static void main(String[] args) {
int[] a = {3,2,4,1,5};
int n = a.length;
System.out.println("该集合A为:"+ Arrays.toString(a)+",集合A的元素个数N为:"+n);
smallPartition divide = divide(a);
System.out.println("从集合A第"+divide.position+"个位置进行划分"+"集合A1为:"+divide.A1+"集合A2为:"+divide.A2);
System.out.println("集合A1的元素个数N1为:"+divide.position+" ,集合A2的元素个数N2为:"+(n-divide.position)+",那|N1-N2|为:"+Math.abs(divide.position-(n-divide.position)));
System.out.println("集合A1的元素之和S1为:"+divide.sum1+" ,集合A2的元素之和为:"+divide.sum2+",那|S1-S2|为:"+Math.abs(divide.sum1-divide.sum2));
}
/**
*找到符合条件的分区位置
* @param a 要划分的数组A
* @param s 数组A的第一个元素下标 start
* @param f 数组A的最后一个元素的下标 final
* @return 返回中间位置
*/
public static int partition(int[] a,int s,int f){//快速排序中的分区
int pivot = a[s];//基准
while (s=pivot)
f--;
a[s] = a[f];
while (f>s && a[s]<=pivot)
s++;
a[f] = a[s];
}
a[s] = pivot;
return s;//返回中间位置
}
static class smallPartition{//分别存放集合A1和集合A2
int position =-1;//集合A从position处划分集合A1和集合A2
ArrayList A1 = new ArrayList();//用ArrayList存放集合A1
ArrayList A2 = new ArrayList();//用ArrayList存放集合A2
int sum1=0;//A1之和
int sum2 =0;//A2之和
public smallPartition() {//无参构造
}
}
//将集合A划分成集合A1和集合A2
public static smallPartition divide(int[] a ){
int n = a.length;//集合A中元素的个数
int s = 0,f = n-1;//s:start,集合A中的第一个下标;f:final,集合A中最后一个下标
smallPartition smallPartition = new smallPartition();//初始化A1和A2
int position = -1;//初始化中间位置
while (s 3、结果
4、复杂度
平均复杂度为O(n),空间复杂度为O(1);
四、折半查找
1、描述
折半查找,也称二分查找、二分搜索,是一种在有序数组中查找某一特定元素的搜索算法。搜素过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜素过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组已经为空,则表示找不到指定的元素。这种搜索算法每一次比较都使搜索范围缩小一半,其时间复杂度是O(logN)。
2、代码实现
/**
* @description:折半查找,递归实现
* @author: fayoung
* @time: 2022/3/16 16:16
*/
public class HalfSearch {
public static void main(String[] args) {
int[] a={2,4,6,7,9,13,36};
int key = 7;
int position = halfSearch(a,key,0,a.length-1);
System.out.println("在该数组:"+ Arrays.toString(a)+"中查找"+key+"在第几个位置");
System.out.println(key+"在该数组的第"+(position+1)+"个位置");
}
/**
*
* @param a:要查找数所在的数组
* @param key:要查找的数
* @param s:数组的第一个下标
* @param f:数组的最后一个下标
* @return 返回数组中第几个数为要查找的数
*/
public static int halfSearch(int[] a,int key,int s,int f){
int mid = s+(s+f)/2;//中间位置
if (a[mid] == key){
return mid;
}else if (a[mid]3、结果
五、查找第k小元素
1、描述
查找一个数组中的第k小元素
2、代码实现
/**
* @description:查找第k小元素
* @author: fayoung
* @time: 2022/3/16 16:57
*/
public class FindKth {
public static void main(String[] args) {
int[] a = {3,4,1,2,5};//要查找元素所在数组
int k = 2;//第几小
System.out.println("在该数组:"+Arrays.toString(a)+"中查找第"+k+"小的元素为:"+FindKth(a,k));
}
/**
* 在数组a中,查找第k小的元素,整体的思想为通过分治的思想返回要查找元素所在的分区
* @param a 查找的数组
* @param k 查找元素的第几大
* @return 返回第k大的元素
*/
public static int FindKth(int a[],int k){
int s =0;
int f = a.length-1;
while (s pivot)
f--;
a[s] = a[f];
while (f > s && a[s] < pivot)
s++;
a[f] = a[s];
}
a[s] = pivot;
return s;
}
} 3、结果
六、寻找两个等长有序序列的中位数
1、描述
给定两个有序序列,找到这两个有序序列的中位数
2、代码实现
/**
* @description:寻找两个等长有序序列的中位数
* @author: fayoung
* @time: 2022/3/20 21:50
*/
public class Find2ListMid {
public static void main(String[] args) {
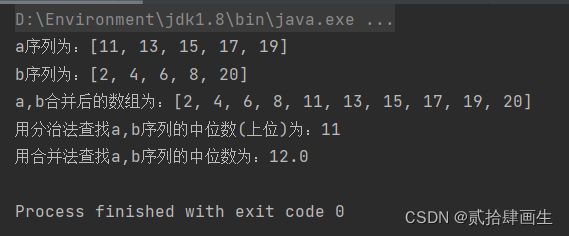
int a[] ={11,13,15,17,19};
int b[] = {2,4,6,8,20};
System.out.println("a序列为:"+ Arrays.toString(a));
System.out.println("b序列为:"+ Arrays.toString(b));
System.out.println("a,b合并后的数组为:"+Arrays.toString(Merge2List(a,b)));
System.out.println("用分治法查找a,b序列的中位数(上位)为:"+FindMidByBinary(a,0,a.length-1,b,0,b.length-1));
System.out.println("用合并法查找a,b序列的中位数为:"+FindMidByMerge(a,b));
}
//采用分治的思想解决
/**
* 整体的思想为利用分治的思想找到两个序列的中位数,再比较这两个中位数,进而确定整个序列中位数的位置
* 对于含有n个,元素的有序序列a[s … t ],
*
* 当n为奇数时,中位数出现在m=(s+t)/2;
* 当n为偶数时,中位数出现在m=(s+t)/2上中位和m=(s+t)/2+1下中位;在这里假设只取上中位
*
* (1)分别求a、b的中位数a[m1]和b[m2]
* (2)若a[m1]=b[m2],则a[m1]和b[m2]即为所求中位数
* (3)若a[m1]b[m2],则舍弃a中的后半部分,同时舍弃b的前半部分,两端舍弃部分的长度要相等
*
* 在保留的两个升序序列中重复上述过程,直到两个序列中只含有一个元素为止,较小者即为所求的中位数。
*/
/**
* 求序列的前半子序列
* @param s start 数组起始位置
* @param f final 数组末尾位置
*/
public static void pre(int s,int f){
int m = (s+f)/2; //中间位置
f=m;//前半序列的最后一个下标
}
/**
* 求序列的后半子序列
* @param s start 起始位置
* @param f final 末尾位置
* [1,2,3,4,5] 该序列为奇数个,pre[1,2,3] last[3,4,5]
* [1,2,3,4] 该序列为偶数个 ,pre[1,2] last[3,4]
*/
public static void last(int s,int f){
int m = (s+f)/2;
if ((s+f)%2 == 0)//如果是奇数个元素
s=m;
else
s=m+1;//偶数
}
/**
* 利用分治的思想,查找中位数
* @param a a序列
* @param s1 a序列的首个下标
* @param f1 a序列的最后一个下标
* @param b b序列
* @param s2 b序列的第一个下标
* @param f2 b序列的最后一个下标
* @return a b序列的中位数
*/
public static int FindMidByBinary(int[] a,int s1,int f1,int[] b,int s2,int f2){
int m1,m2;
if (s1==s2&&f1==f2){//如果两个数组均只有1个元素,这个数就是中位数
return a[s1];
}else {
m1 = (s1+f1)/2;//a序列的中间位置
m2 = (s2+f2)/2;//b序列的中间位置
if (a[m1] == a[m2]){//如果两个中位数相等,则就是整个序列的中位数
return a[m1];
}else if(a[m1] 3、结果
七、归并排序
1、描述
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
2、代码实现
/**
* @description:归并排序,利用分治的思想进行数组的排序(递归实现)
* 1、将n个元素从中间分开,分为左分区和右分区
* 2、将左分区和右分区再分别递归,直到分区里只有一个元素
* 3、从最后一层的分区逐步合并两个有序分区
* @author: fayoung
* @time: 2022/3/21 10:13
*/
public class MergeSort {
public static void main(String[] args) {
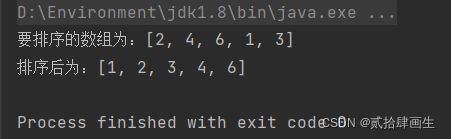
int[] a ={2,4,6,1,3};
System.out.println("要排序的数组为:"+Arrays.toString(a));
mergeSort(a,0,a.length-1);
System.out.println("排序后为:"+Arrays.toString(a));
}
/**
* 合并两个有序数组
* @param arr 要排序的数组
* @param start arr数组的第一个下标
* @param mid arr数组的中间下标
* @param end arr数组的最后一个下标
*/
public static void Merge(int[] arr,int start, int mid,int end){
int[] temp = new int[arr.length]; //一个临时数组temp,用于存放合并后的有序数组
int start1 = start;//左边分区的第一个下标,最后一个下标为mid,相当于左边分区的指针
int start2 = mid+1;//右边分区的第一个下标,最后一个下标为end,相当于右边分区的指针
int k =0;//表示temp数组的下标,相当于temp数组的指针
while (start1<=mid && start2<=end){//当左右分区的指针都在分区里面时
if (arr[start1]=end){ //递归的结束条件
return;
}
int mid =start + ((end-start)/2);//数组的中间位置
mergeSort(arr,start,mid);//递归归并左边分区
mergeSort(arr,mid+1,end);//递归归并右边分区
Merge(arr,start,mid,end);//再将两个有序数组合并
}
} 3、结果
八、折半查找的拓展
1、描述
设有n个互不相同的整数,按递增顺序存放在数组a[0,n-1]中,若存在一个下标i,满足a[i]=i,设计一个log2N的的算法找到
2、代码实现
/**
* @description:折半查找的拓展:设有n个互不相同的整数,按递增顺序存放在数组a[0,n-1]中,若存在一个下标i,满足a[i]=i,设计一个log2N的的算法找到
* @author: fayoung
* @time: 2022/3/23 11:27
*/
public class FindI {
public static void main(String[] args) {
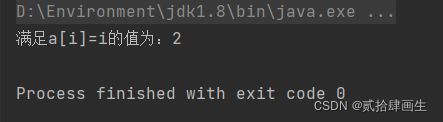
int[] a = {-2,-1,2,4,6,8,9};
int i = findI(a);
if (i!=-1)
System.out.println("满足a[i]=i的值为:"+i);
else
System.out.println("该数组中不存在");
}
/**
* 思路就是折半查找,a[i]=i是一个条件,要在一组数中找到符合条件的值,就折半查找效率最高
* @param arr 查找的数组
* @return 符合条件的值,或-1(表示不存在)
*/
public static int findI(int[] arr){
int start =0,end = arr.length-1;//数组的第一个下标和最后一个下标
int mid;//中间位置
while (start<=end){//结束条件
mid = (start+end)/2;//中间位置,折半
if (arr[mid]==mid)//如果a[i]=i,则返回i
return mid;
else if (arr[mid]i,说明要找的数在左边
end = mid-1;
}
return -1;
}
} 3、结果
九、最大序列和(分治法)
1、描述
用分治法解决最大序列和问题
2、代码实现
/**
* @description:用分治法解决最大序列和问题
* @author: fayoung
* @time: 2022/3/23 23:04
*/
public class MaxSumByDivide {
public static void main(String[] args) {
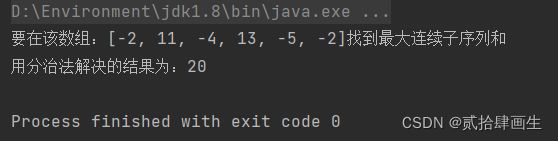
int[] a = {-2,11,-4,13,-5,-2};
int n = a.length;
System.out.println("要在该数组:"+ Arrays.toString(a)+"找到最大连续子序列和");
System.out.println("用分治法解决的结果为:"+maxSumByDivideAndConquer(a,0,n-1));
}
public static int maxSumByDivideAndConquer(int[] arr,int low,int high){
int sum =0;
if (low==high){
return sum= arr[low];
}else {
int mid = (low+high)/ 2;
int leftMax = maxSumByDivideAndConquer(arr, low, mid);//左边分区
int rightMax = maxSumByDivideAndConquer(arr, mid + 1, high);
//计算包含左侧子序列最后一个元素的子序列的最大值
int leftListMax = Integer.MIN_VALUE;
int leftListSum = 0;
for (int i = mid; i >=low; i--) {
leftListSum +=arr[i];
leftListMax = Math.max(leftListSum,leftListMax);
}
//计算包含右侧子序列的第一个元素的子序列最大值
int rightListMax = arr[mid+1];
int rightListSum = 0;
for (int i = mid+1; i <=high; i++) {
rightListSum+=arr[i];
rightListMax = Math.max(rightListMax,rightListSum);
}
//计算中间的子序列的最大值
int listMax = leftListMax+rightListMax;
return Math.max(listMax,Math.max(leftMax,rightMax));
}
}
}3、结果
第四章 蛮力法
一、找数字
1、描述
找到一个4位数,千位和百位被擦除,知道十位上是1,个位是2,且如果这个数n-7可以整除7,这个数n-8可以整除8,这个数n-9可以整除9
2、代码实现
/**
* @description:找到一个4位数,千位和百位被擦除,知道十位上是1,个位是2,且如果这个数n-7可以整除7,这个数n-8可以整除8,这个数n-9可以整除9
* @author: fayoung
* @time: 2022/3/21 11:41
*/
public class FindNumber {
public static void main(String[] args) {
int n;
for (int a =1;a<=9;a++){
for (int b =0;b<=9;b++){
n=1000*a+100*b+10+2;
if ((n-7)%7 == 0&& (n-8)%8==0&&(n-9)%9==0) {
System.out.println("满足”千位和百位被擦除,知道十位上是1,个位是2,且如果这个数n-7可以整除7,这个数n-8可以整除8,这个数n-9可以整除9“" +
"条件的数为"+n);
}
}
}
}
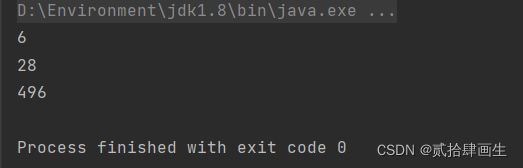
}
3、结果
二、完美数
1、描述
如果一个数恰好等于它的真因子(又叫“真因数”,即除了自身以外的约数)之和,则称该数为完全数,又称完美数或完备数。
2、代码实现
public class PerfectNumber {
/**
* @description: 查找完全数,数本身会等于其所有因子之和
* @author: fayoung
* @time: 2022/3/21 11:28
*/
public static void main(String[] args) {
for (int i = 2; i < 1000; i++) {
int sum = 0;
//查找因数
for (int j = 1; j < i; j++) {
if (i % j == 0) {
sum += j;
}
}
if (sum == i)
System.out.println(i);
}
}
}3、结果
三、数列分段
1、描述
给定一整数数列,数列中连续相同的最长整数序列算成一段,问数列中共有多少段?
2、代码实现
/**
* @description:数列分段:
* 问题描述:给定一整数数列,数列中连续相同的最长整数序列算成一段,问数列中共有多少段?
* 输入格式:输入的第一行包含一个整数n,表示数列中整数的个数。
* 第二行包含n个整数a1,a2....an,表示给定的数列,相邻的整数之问用一个空格分隔
* @author: fayoung
* @time: 2022/3/23 13:12
*/
public class SequenceSegment {
public static void main(String[] args) throws IOException {
int[] a ={8,8,8,0,12,12,8,0};
int n = a.length;
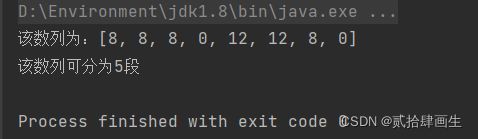
System.out.println("该数列为:"+ Arrays.toString(a));
System.out.println("该数列可分为"+sequenceSegment(a, n)+"段");
}
public static int sequenceSegment(int[] a ,int n){
int temp= Integer.MIN_VALUE;
int count=0;
for (int i = 0; i 3、结果
四、最大子序列和(蛮力法)--3种实现方法
1、问题描述
用蛮力法解决最大连续子序列问题
2、代码实现
/**
* @description:用蛮力法解决最大连续子序列问题
* @author: fayoung
* @time: 2022/3/21 10:37
*/
public class MaxSumByBrute {
public static void main(String[] args) {
int[] a = {-2,11,-4,13,-5,-2};
int n = a.length;
System.out.println("要在该数组:"+Arrays.toString(a)+"找到最大连续子序列和");
System.out.println("用蛮力法1解决的结果为:"+maxSumByBrute1(a,n));
System.out.println("用蛮力法2解决的结果为:"+maxSumByBrute2(a,n));
System.out.println("用蛮力法3解决的结果为:"+maxSumByBrute3(a,n));
}
/**
* 用蛮力法解决最大子序列和问题
* @param a 要查找的数组a
* @param n 数组的长度
* @return
*/
public static int maxSumByBrute1(int[] a,int n){
int maxSum = 0;
int curSum;
for (int i = 0; i maxSum)
maxSum=curSum;
}
}
return maxSum;
}
public static int maxSumByBrute2(int[] a,int n){
int maxSum = 0;
int curSum;
for (int i = 0; i maxSum)
maxSum=curSum;
}
}
return maxSum;
}
public static int maxSumByBrute3(int[] a,int n){
int maxSum=0,curSum =0;
int[] temp = new int[a.length];
for (int i = 0; i < n; i++) {
curSum+=a[i];
if (curSum<0)
curSum=0;
if (maxSum 3、结果
五、 最小差值
1、问题描述
给定n个数,请找出其中相差(差的绝对值)最小的两个数,输出它们的差值的绝对值。
2、代码实现
/**
* @description:最小差值:给定n个数,请找出其中相差(差的绝对值)最小的两个数,输出它们的差值的绝对值。
* @author: fayoung
* @time: 2022/3/23 13:35
*/
public class MinimumDifference {
public static void main(String[] args) {
int[] a = {1,5,4,8,20};
int n = a.length;
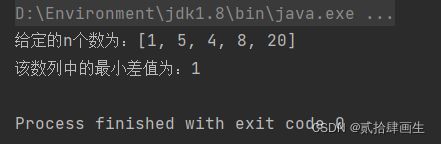
System.out.println("给定的n个数为:"+ Arrays.toString(a));
System.out.println("该数列中的最小差值为:"+minimumDifference(a,n));
}
public static int minimumDifference(int[] a,int n){
int temp = Integer.MAX_VALUE;//temp是一个临时变量,设初值为最大值
for (int i = 0; i 3、结果
六、相邻数对
1、问题描述
给定n个不同的整数,问这些数中有多少对整数,他们的值正好相差1
2、代码实现
/**
* @description:相邻数对:给定n个不同的整数,问这些数中有多少对整数,他们的值正好相差1
* @author: fayoung
* @time: 2022/3/23 14:56
*/
public class AdjacentPairs {
public static void main(String[] args) {
int[] a = {10,2,6,3,7,8};
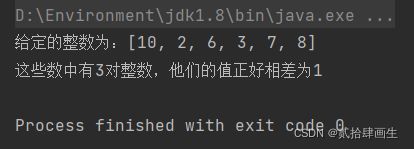
System.out.println("给定的整数为:"+ Arrays.toString(a));
System.out.println("这些数中有"+adjacentPairs(a)+"对整数,他们的值正好相差为1");
}
public static int adjacentPairs(int[] a){
int count =0;
for (int i = 0; i 3、结果
七、报数游戏
1、问题描述
有n个小朋友围成一圈玩游戏,小朋友从1至n编号,2号小朋友坐在1号小朋友的顺时针方向,3号小朋友坐在2号小朋友的顺时针方向,……,1号小朋友坐在n号小朋友的顺时针方向 游戏开始,从1号小朋友开始顺时针报数,接下来每个小朋友的报数是上一个小朋友报的数加1。若一个小朋友报的数为k的倍数或其末位数(即数的个位)为k, 则该小朋友被淘汰出局,不再参加以后的报数。当游戏中只剩下一个小朋友时,该小朋友获胜。
2、代码实现
/**
* @description:报数游戏
* @author: fayoung
* @time: 2022/3/23 16:49
*/
public class CallNumber {
public static void main(String[] args) {
System.out.println(callNumber(5,2)+"小孩获胜");
}
/**
* 利用队列的性质,判断报数成员的编号和k之间的关系,不符合条件的出队,符合条件的重新入队
* @param n 参加游戏的人数
* @param k 特殊的数字
* @return 队列中最后一个成员的编号
*/
public static int callNumber(int n,int k) {
if (n == 1 || k == 1)
return n;
Queue queue = new LinkedList<>();
for (int i = 1; i <= n; i++) {
queue.offer(i); //入队
}
int order = 0; //报数的次序
int current = 0; //当前报数成员的编号
while (queue.size() > 0) {
current = queue.poll();
if (queue.size() == 0) break;
order++;
if (order % k != 0 && order % 10 != k) { //末尾不是k并且不被k整除,重新入队
queue.offer(current);
}
}
return current;
}
}
3、结果
八、简单选择排序
1、问题描述
选择排序(Selection Sort)是一种简单直观的排序算法。 它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。 以此类推,直到全部待排序的数据元素的个数为零。
2、代码实现
/**
* @description:j简单选择排序
* @author: fayoung
* @time: 2022/3/23 13:49
*/
public class SelectSort {
public static void main(String[] args) {
int [] a= { 49,38,65,97,76,13,27,49 };
System.out.println("排序前:"+Arrays.toString(a));
selectSort(a);
System.out.println("排序后:"+Arrays.toString(a));
}
public static void selectSort(int[] a){
for (int i = 0; i 3、结果
九、冒泡排序
1、问题描述
冒泡排序(Bubble Sort)也是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。
2、代码实现
/**
* @description:冒泡排序
* @author: fayoung
* @time: 2022/3/23 14:32
*/
public class BubbleSort {
public static void main(String[] args) {
int [] a= { 49,38,65,97,76,13,27,49 };
System.out.println("排序前:"+ Arrays.toString(a));
bubbleSort(a);
System.out.println("排序后:"+Arrays.toString(a));
}
public static void bubbleSort(int[] a){
for (int i = 0; i < a.length; i++) {
for (int j = 1; j < a.length-i; j++) {
if (a[j-1]>a[j]){//如果前面的数字大于后面的数字就进行交换
int temp;
temp = a[j-1];
a[j-1] = a[j];
a[j] = temp;
}
}
}
}
}3、结果
十、字符串匹配
1、描述
判断字符串是否匹配,并计算出现次数
2、代码实现
/**
* @description:字符串匹配:对于字符串s和t,若t是s子串,返回t在s中的位置(t的首字符在s中对应的下标),否则返回-1。并统计出现词搜
* @author: fayoung
* @time: 2022/3/23 15:06
*/
public class StringMatch {
public static void main(String[] args) {
String a ="aababcde";
String b= "abcd";
System.out.println("判断b是否是a的子串");
System.out.println("a字符串为:"+a);
System.out.println("b字符串为:"+b);
int position = stringMatchByBF(a.toCharArray(),b.toCharArray());
int count = count(a.toCharArray(),b.toCharArray());
if (position!=-1)
System.out.println("b是a的子串,从a字符串的第"+(position+1)+"个位置开始匹配,出现了"+count+"次");
else
System.out.println("b不是a的子串");
}
/**
* 字符串匹配
* @param a 字符数组a
* @param b 字符数组b,判断b是否是a的子串
* @return 如果是字串,返回b在a中的位置
*/
public static int stringMatchByBF(char[] a,char[] b){
int i =0,j=0;//相当于a,b字符数组中的两个指针
while (i3、结果