记录kitti数据集的坐标系转换问题
Calib文件说明
以00000.txt文件为例,详细介绍每行含义
P0: 7.070493000000e+02 0.000000000000e+00 6.040814000000e+02 0.000000000000e+00 0.000000000000e+00 7.070493000000e+02 1.805066000000e+02 0.000000000000e+00 0.000000000000e+00 0.000000000000e+00 1.000000000000e+00 0.000000000000e+00
P1: 7.070493000000e+02 0.000000000000e+00 6.040814000000e+02 -3.797842000000e+02 0.000000000000e+00 7.070493000000e+02 1.805066000000e+02 0.000000000000e+00 0.000000000000e+00 0.000000000000e+00 1.000000000000e+00 0.000000000000e+00
P2: 7.070493000000e+02 0.000000000000e+00 6.040814000000e+02 4.575831000000e+01 0.000000000000e+00 7.070493000000e+02 1.805066000000e+02 -3.454157000000e-01 0.000000000000e+00 0.000000000000e+00 1.000000000000e+00 4.981016000000e-03
P3: 7.070493000000e+02 0.000000000000e+00 6.040814000000e+02 -3.341081000000e+02 0.000000000000e+00 7.070493000000e+02 1.805066000000e+02 2.330660000000e+00 0.000000000000e+00 0.000000000000e+00 1.000000000000e+00 3.201153000000e-03
R0_rect: 9.999128000000e-01 1.009263000000e-02 -8.511932000000e-03 -1.012729000000e-02 9.999406000000e-01 -4.037671000000e-03 8.470675000000e-03 4.123522000000e-03 9.999556000000e-01
Tr_velo_to_cam: 6.927964000000e-03 -9.999722000000e-01 -2.757829000000e-03 -2.457729000000e-02 -1.162982000000e-03 2.749836000000e-03 -9.999955000000e-01 -6.127237000000e-02 9.999753000000e-01 6.931141000000e-03 -1.143899000000e-03 -3.321029000000e-01
Tr_imu_to_velo: 9.999976000000e-01 7.553071000000e-04 -2.035826000000e-03 -8.086759000000e-01 -7.854027000000e-04 9.998898000000e-01 -1.482298000000e-02 3.195559000000e-01 2.024406000000e-03 1.482454000000e-02 9.998881000000e-01 -7.997231000000e-01
P0~P4
P0~P4 可以称作相机投影矩阵 ,是由相机一系列内参组成。0~4表示4个相机编号,其中0、1是灰度相机,3、4是彩色相机(分别对应左右两幅图形)。投影矩阵 P ( i ) r e c t P{(i) \atop rect} Prect(i)的每个数值的含义如下:
P ( i ) r e c t = ( f ( i ) u 0 c i u − f ( i ) u b i x 0 f ( i ) v c i v 0 0 0 0 1 ) P{(i) \atop rect} = \Biggl(\def\arraystretch{1.5} \begin{array}{cc} f{(i) \atop u} & 0 & c{i \atop u} & -f{(i) \atop u}b{i \atop x} \\ 0 & f{(i) \atop v} & c{i \atop v} & 0 \\ 0 &0&0&1 \end{array}\Biggr) Prect(i)=(fu(i)000fv(i)0cuicvi0−fu(i)bxi01)
f ( i ) u , f ( i ) v f{(i) \atop u},f{(i) \atop v} fu(i),fv(i) 是第i幅图像的焦距 (调整镜头前后缩进)
c ( i ) u , c ( i ) v c{(i) \atop u},c{(i) \atop v} cu(i),cv(i) 是第i幅图像的主点偏移 (左右成像平面大小)
b i x b{i \atop x} bxi 是第i号相机到第0号相机的x方向的距离偏移
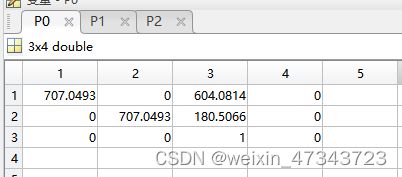
现将P0可视化 :
# matlab
P0 = [7.070493000000e+02 0.000000000000e+00 6.040814000000e+02 0.000000000000e+00 0.000000000000e+00 7.070493000000e+02 1.805066000000e+02 0.000000000000e+00 0.000000000000e+00 0.000000000000e+00 1.000000000000e+00 0.000000000000e+00]
P0 = reshape(P0,4,3)
P0 = P0'
矩阵作用: 用于将3D相机坐标系转为2D图像坐标系(成像物理坐标系),具体公式如下:
Y = P r e c t ( i ) X Y=P_{rect}^{(i)}X Y=Prect(i)X
此外,还需要进行矩阵矫正,因此公式变换为:(此前一直以为是只矫正0号相机,其实不是,所有相机都要乘上这个矩阵)
Y = P r e c t ( 0 ) R r e c t ( 0 ) X Y=P_{rect}^{(0)}R_{rect}^{(0)}X Y=Prect(0)Rrect(0)X
其中, X 4 ∗ 1 X_{4*1} X4∗1是相机坐标系下的坐标,X=(Xc,Yc,Zc,1), R 4 ∗ 4 R_{4*4} R4∗4是0号相机的修正矩阵,可视化结果如下,最后一列一行是增加上去的, P r e c t ( 0 ) ∈ R 3 ∗ 4 P_{rect}^{(0)}\in\reals^{3*4} Prect(0)∈R3∗4,Y=(u,v,1)。
Q: 为什么X维度是4呢?
A:这要从上一步坐标变换说起——从点云坐标系到相机坐标系的转换过后,便获得了上述维度的X,至于怎么变换的,下面会展开来讲。
R0_rect
一个3X3的矩阵,不需要加行或者列,已介绍过,此处不再赘述
Tr_velo_to_cam
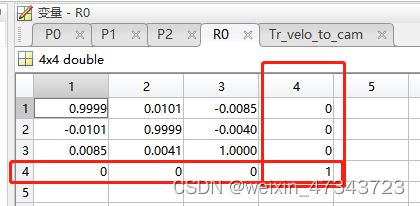
将点云转为3D坐标系需要用到如下矩阵:(可以理解为相机外参?,假如世界坐标系与点云坐标系重合,应该可以这么理解),对其可视化后如图所示,其中最后一行(0,0,0,1)是添加上的。

定义: Tr_velo_to_cam是由旋转矩阵+平移矩阵构成,具体含义如下:
T r _ v e l o _ t o _ c a m = [ R ∣ t ] = [ r 1 , 1 r 1 , 2 r 1 , 3 t 1 r 2 , 1 r 2 , 2 r 2 , 3 t 2 r 3 , 1 r 3 , 2 r 3 , 3 t 3 ] Tr\_velo\_to\_cam=[R|t]=\begin{bmatrix} r_{1,1} & r_{1,2} &r_{1,3}&t_1 \\ r_{2,1} & r_{2,2} &r_{2,3}&t_2 \\ r_{3,1} & r_{3,2} &r_{3,3}&t_3 \\ \end{bmatrix} Tr_velo_to_cam=[R∣t]=⎣ ⎡r1,1r2,1r3,1r1,2r2,2r3,2r1,3r2,3r3,3t1t2t3⎦ ⎤
可以看到 T r _ v e l o _ t o _ c a m ∈ R 3 ∗ 4 Tr\_velo\_to\_cam\in\reals^{3*4} Tr_velo_to_cam∈R3∗4,因此对点云坐标X=[X,Y,Z]补1得到4行1列矩阵X=[X,Y,Z,1]。这么做的原因不仅是要满足矩阵相乘时的维度对齐,还可以保证加上常数项实施平移操作。为方便理解,可以举个例子: 此处参考链接——包含知识点:世界坐标系到相机坐标系的转换、齐次坐标系
情况1:仅旋转
对(x,y,z)进行旋转操作,若为3*3的矩阵,则只能进行旋转操作,而没有平移操作,所以需要加上常数项,即:将三维的笛卡尔坐标添加一个额外坐标,就可以实现坐标平移,而且保持了三维向量与矩阵乘法具有的缩放和旋转操作。这个就称为齐次坐标,而这种变换也称为仿射变换(affine transformation)。详细操作如下:
[ 1 0 0 0 0 2 0 1 0 ] [ x y z ] = [ x 2 z y ] \begin{bmatrix} 1 & 0 &0 \\ 0 & 0 &2 \\ 0 & 1&0 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ \end{bmatrix}=\begin{bmatrix} x \\ 2z \\ y \\ \end{bmatrix} ⎣ ⎡100001020⎦ ⎤⎣ ⎡xyz⎦ ⎤=⎣ ⎡x2zy⎦ ⎤
情况2:旋转+平移
[ 1 0 0 0 0 0 2 0 0 1 0 3 0 0 0 1 ] [ x y z 1 ] = [ x 2 z y + 3 1 ] \begin{bmatrix} 1 & 0 &0 &0 \\ 0 & 0 &2 & 0\\ 0 & 1&0 & 3\\ 0 & 0&0 & 1\\ \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}=\begin{bmatrix} x \\ 2z \\ y +3\\ 1 \end{bmatrix} ⎣ ⎡1000001002000031⎦ ⎤⎣ ⎡xyz1⎦ ⎤=⎣ ⎡x2zy+31⎦ ⎤
因此,对于一个n*3的点云,首先要添加1列。对于点云坐标系到2D图像坐标系的变换公式如下:
Y = P r e c t ( i ) T r _ v e l o _ t o _ c a m 4 ∗ 4 X Y=P_{rect}^{(i)}Tr\_velo\_to\_cam_{4*4} X Y=Prect(i)Tr_velo_to_cam4∗4X
Tr_imu_to_velo
与Tr_velo_to_cam类似,不再赘述。
总结:
| P0~P4 | Tr_velo_to_cam |
|---|---|
| 相机内参 | 相机外参 |
| 3D相机坐标系(x,y,z,1) —>2D图像(u,v,1) | 世界坐标系/点云坐标系(X,Y,Z,1) —>3D相机坐标系(x,y,z,1) |
| 维度不变 3*4 | 添加维度 3*4到4*4 |
Tr_velo_to_cam称为外参矩阵,由旋转+平移矩阵构成,为了保证维度,需要同时对点云和矩阵进行升维。总之,就是一个内参、一个外参,一个不加维度,一个变为4*4,相应的数据也都跟着多了一维。看起来似乎很简单,但我还是看了好几天。
可视化
昨天发现了一个很有意思的可视化代码,通过代码发现自己的理解还是有问题,所以下面详细介绍实现过程,包括:
- 点云投影到2D图像
- 3Dbox在点云上的投影
目前只看了这两部分,其他功能有待发现,在这里先放上 Github链接。
安装
这里先讲一下我的环境:Win10+python 3.8,我没有按照作者给的方式安装,因为会报错。mayavi包总是很难安装,还好之前也写了篇博客,不然又摸索很久。
conda create -n kitti_vis python=3.8
conda activate kitti_vis
pip install opencv-python pillow scipy matplotlib
pip install vtk==9.0.1
pip install mayavi==4.7.3
pip install PyQt5
几分钟应该就可以配置完环境,接下来运行以下代码测试
python kitti_object.py --show_lidar_with_depth --img_fov --const_box --vis
就会出现两个可视化结果,这里展示的是第二个数据:
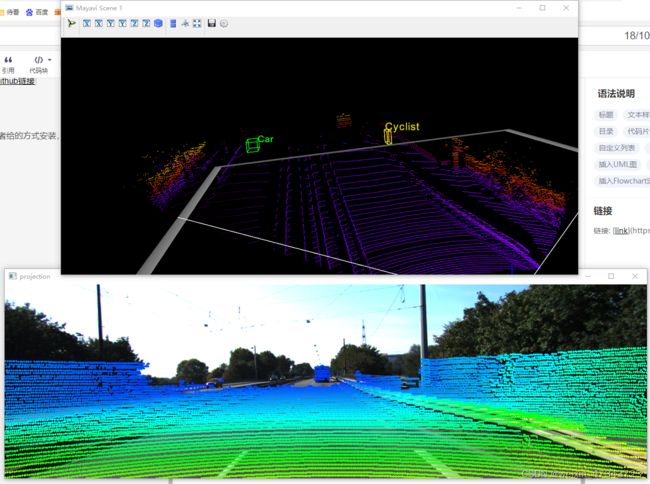
此次再记录一个windows下使用vscode没办法切换配置环境的问题

使用右边框框换新的终端(我也不太懂),参考链接
投影转换代码
先筛选点云范围,对应到图像上时要小于等于图像的长和宽,大于0
思路: 点云 → \rightarrow → 3D Camera 先添1列,乘外参矩阵,乘R0
# 外参
def project_velo_to_ref(self, pts_3d_velo):
pts_3d_velo = self.cart2hom(pts_3d_velo) # nx4
return np.dot(pts_3d_velo, np.transpose(self.V2C)) # 外参 3*4
# R0
def project_ref_to_rect(self, pts_3d_ref):
""" Input and Output are nx3 points """
return np.transpose(np.dot(self.R0, np.transpose(pts_3d_ref)))
def project_velo_to_rect(self, pts_3d_velo):
pts_3d_ref = self.project_velo_to_ref(pts_3d_velo)
return self.project_ref_to_rect(pts_3d_ref)
project_velo_to_rect(lidar) #调用
3D Camera → \rightarrow → 2D image
def project_rect_to_image(self, pts_3d_rect):
""" Input: nx3 points in rect camera coord.
Output: nx2 points in image2 coord.
"""
pts_3d_rect = self.cart2hom(pts_3d_rect)
pts_2d = np.dot(pts_3d_rect, np.transpose(self.P)) # nx3
pts_2d[:, 0] /= pts_2d[:, 2]
pts_2d[:, 1] /= pts_2d[:, 2]
return pts_2d[:, 0:2]