动态规划基础题目-代码随想录-刷题笔记
基础理论
什么是动态规划:Dynamic Programming
动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,
贪心没有状态推导,而是从局部直接选最优的,
记住:动规是由前一个状态推导出来的,而贪心是局部直接选最优
动态规划的解题步骤
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
动态规划应该如何debug
找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!
做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果。
509. 斐波那契数
法一:递归
//时间复杂度:O(2^n)
//空间复杂度:O(n),递归的系统栈所占空间
class Solution {
public:
int fib(int n) {
if(n<=1){
return n;
}
return fib(n-1)+fib(n-2);
}
};
法二:动规
- 确定dp数组(dp table)以及下标的含义
dp[i]:第i个数的斐波那契数值是dp[i]
- 确定递推公式
dp[i]=dp[i-1]+dp[i-2]
- dp数组如何初始化
dp[0]=0,dp[1]=1,dp[2]=1
- 确定遍历顺序
从前往后
- 举例推导dp数组
n: 0 1 2 3 4 5 6
dp[n]:0 1 1 2 3 5 8
//时间复杂度:O(n)
//空间复杂度:O(n)
class Solution {
public:
int fib(int N) {
if (N <= 1) return N;
vector<int> dp(N + 1);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= N; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[N];
}
};
空间优化
只需要维护两个数值就可以了,不需要记录整个序列。
class Solution {
public:
int fib(int N) {
if (N <= 1) return N;
int dp[2];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= N; i++) {
int sum = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = sum;
}
return dp[1];
}
};
70. 爬楼梯
法一,递归超时
class Solution {
public:
int climbStairs(int n) {
if(n<=3){
return n;
}
return climbStairs(n-1)+climbStairs(n-2);
}
};
法二:动态规划
- 确定dp数组(dp table)以及下标的含义
dp[i]:爬山不n阶楼有dp[i]种方法
- 确定递推公式
dp[i]=dp[i-1]+dp[i-2]
- dp数组如何初始化
dp[1]=1,dp[2]=2,dp[3]=3
- 确定遍历顺序
从前往后
-
举例推导dp数组
n:0 1 2 3 4 5 6
dp[i]:1 1 2 3 5 8 13
//时间复杂度:O(n)
//空间复杂度:O(n)
class Solution {
public:
int climbStairs(int n) {
vector<int>dp(n+1,0);
if(n<=2) return n;
dp[1]=1;
dp[2]=2;
for(int i=3;i<n+1;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
};
空间优化
class Solution {
public:
int climbStairs(int n) {
if(n<=2) return n;
int a=1;
int b=2;
for(int i=3;i<n+1;i++){
int sum=a+b;
a=b;
b=sum;
}
return b;
}
};
746. 使用最小花费爬楼梯
- 确定dp数组(dp table)以及下标的含义
dp[i]:爬到第i台阶所花费的最小体力为dp[i]
- 确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
- dp数组如何初始化
说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
- 确定遍历顺序
从前到后
- 举例推导dp数组
cost楼顶: 1 100 1 1 1 100 1 1 100 1
下标: 0 1 2 3 4 5 6 7 8 9 10
dp[i]: 0 0 1 2 2 3 3 4 4 5 6
//时间复杂度:O(n)
//空间复杂度:O(n)
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size() + 1);
dp[0] = 0; // 默认第一步都是不花费体力的
dp[1] = 0;
for (int i = 2; i <= cost.size(); i++) {
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[cost.size()];
}
};
空间优化
/ 版本二
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int dp0 = 0;
int dp1 = 0;
for (int i = 2; i <= cost.size(); i++) {
int dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2]);
dp0 = dp1; // 记录一下前两位
dp1 = dpi;
}
return dp1;
}
};
62. 不同路径
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
dp[i][j]=dp[i-1][j]+dp[i][j-1];
- dp数组如何初始化
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
- 确定遍历顺序
从上到下,从左到右
- 举例推导dp数组,m=3,n=2
0 1
0 1 1
1 1 2
2 1 3
//时间复杂度:O(m × n)
//空间复杂度:O(m × n)
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
空间优化:滚动数组
//时间复杂度:O(m × n)
//空间复杂度:O(n)
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp(n);
for (int i = 0; i < n; i++) dp[i] = 1;
for (int j = 1; j < m; j++) {
for (int i = 1; i < n; i++) {
dp[i] += dp[i - 1];
}
}
return dp[n - 1];
}
};
63. 不同路径 II
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:从(0,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
- dp数组如何初始化
注意代码里for循环的终止条件,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
- 确定遍历顺序
从前到后,从左到右
- 举例推导dp数组,m=3,n=3
0 1 2
0 1 1 1
1 1 0 1
2 1 1 2
//时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
//空间复杂度:O(n × m)
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0
return 0;
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
空间优化
//时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
//空间复杂度:O(m)
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if (obstacleGrid[0][0] == 1)
return 0;
vector<int> dp(obstacleGrid[0].size());
for (int j = 0; j < dp.size(); ++j)
if (obstacleGrid[0][j] == 1)
dp[j] = 0;
else if (j == 0)
dp[j] = 1;
else
dp[j] = dp[j-1];
for (int i = 1; i < obstacleGrid.size(); ++i)
for (int j = 0; j < dp.size(); ++j){
if (obstacleGrid[i][j] == 1)
dp[j] = 0;
else if (j != 0)
dp[j] = dp[j] + dp[j-1];
}
return dp.back();
}
};
343. 整数拆分
贪心
//时间复杂度:O(n)
//空间复杂度:O(1)
class Solution {
public:
int integerBreak(int n) {
if (n == 2) return 1;
if (n == 3) return 2;
if (n == 4) return 4;
int result = 1;
while (n > 4) {
result *= 3;
n -= 3;
}
result *= n;
return result;
}
};
动态规划
- 确定dp数组(dp table)以及下标的含义
dp[i]: 分拆数字i,可以得到的最大乘积是dp[i]
- 确定递推公式
从1遍历j,然后有两种渠道得到dp[i].
一个是j * (i - j) 直接相乘。
一个是j * dp[i - j],相当于是拆分(i - j),对这个拆分不理解的话,可以回想dp数组的定义。
递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
- dp数组如何初始化
dp[0]=0,dp[1]=1,dp[2]=1
- 确定遍历顺序
dp[i] 是依靠 dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。
for (int i = 3; i <= n ; i++) {
for (int j = 1; j < i - 1; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}
- 举例推导dp数组,n=10
i:2 3 4 5 6 7 8 9 10
dp[i]:1 2 4 6 9 12 18 27 36
//时间复杂度:O(n^2)
//空间复杂度:O(n)
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n + 1);
dp[2] = 1;
for (int i = 3; i <= n ; i++) {
for (int j = 1; j <= i / 2; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}
return dp[n];
}
};
96.不同的二叉搜索树
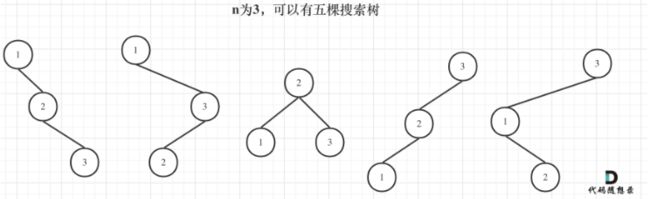
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
- 确定dp数组(dp table)以及下标的含义
dp[i]:1到i为节点组成的二叉搜索树的个数为dp[i]。
- 确定递推公式
dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
- dp数组如何初始化
dp[0]=0
- 确定遍历顺序
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
- 举例推导dp数组
下标i:0 1 2 3
dp[i]:1 1 2 5
//时间复杂度:O(n^2)
//空间复杂度:O(n)
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
};
