算法模板（4）：动态规划（4） 做题积累（2）

动态规划

9. 单调队列优化DP

1. 1088. 旅行问题

John 打算驾驶一辆汽车周游一个环形公路。

公路上总共有 n 个车站，每站都有若干升汽油（有的站可能油量为零），每升油可以让汽车行驶一千米。

John 必须从某个车站出发，一直按顺时针（或逆时针）方向走遍所有的车站，并回到起点。

在一开始的时候，汽车内油量为零，John 每到一个车站就把该站所有的油都带上（起点站亦是如此），行驶过程中不能出现没有油的情况。

任务：判断以每个车站为起点能否按条件成功周游一周。

• 做法：把环形序列扩展一倍成一条链，设距离是 $d_i$，加油站的油量是 $o_i$，打一个 $o_i-d_i$ 的前缀和，从第 $k$ 个点出发可以到达，等价于 $\forall i\in [k,k+n-1],s[i]-s[k-1]\ge 0$，即可以找到长度为 $n$ 的窗口的最小值，然后减去 $s[k-1]$ 看看是否大于等于 0.
• 细节巨多.

#include
using namespace std;
const int N = 2000010;
typedef long long ll;
ll o[N], d[N], s[N];
int q[N], n;
int st[N];

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d%d", &o[i], &d[i]);
    for(int i = 1; i <= n; i++)
    {
        s[i] = s[i + n] = o[i] - d[i];
    }
    for(int i = 1; i <= 2 * n; i++) s[i] += s[i - 1];

    int hh = 0, tt = -1;
    
    //顺时针
    for(int i = 2 * n; i; i--)
    {
        if(q[hh] >= n + i) hh++;
        while(hh <= tt && s[q[hh]] >= s[i]) tt--;
        q[++tt] = i;
        if(i <= n)
        {
            if(s[q[hh]] - s[i - 1] >= 0) st[i] = true;
        }
    }
    
    //逆时针，整个前缀和序列会发生变化
    
    hh = 0, tt = -1;
    d[0] = d[n];
    for(int i = 1; i <= n; i++) s[i] = s[i + n]= o[i] - d[i - 1];
    for(int i = 2 * n; i; i--) s[i] += s[i + 1];
    
    for(int i = 1; i <= 2 * n; i++)
    {
        if(q[hh] <= i - n) hh++;
        while(hh <= tt && s[q[hh]] >= s[i]) tt--;
        q[++tt] = i;
        if(i > n)
        {
            //注意这里是 st[i - n] 
            if(s[q[hh]] - s[i + 1] >= 0) st[i - n] = true;
        }
    }
    
    for(int i = 1; i <= n; i++)
    {
        printf("%s\n", st[i] ? "TAK" : "NIE");
    }
    return 0;
}

2. 1090. 绿色通道

• 高二数学《绿色通道》总共有 $n$ 道题目要抄，编号 $1,2,\dots ,n$，抄第 $i$ 题要花 $a_i$ 分钟。小 Y 决定只用不超过 $t$ 分钟抄这个，因此必然有空着的题。连续空着的题目（称为空题段）越多，老师越生气。小 Y 想让最长的空题段长度尽可能地小，请输出这个最小值.
• 二分一下，就和 烽火传递 思路一样了.

#include
using namespace std;
const int N = 50010;
int q[N], w[N], f[N];
int n, t;

bool check(int m)
{
    int hh = 0, tt = -1;
    q[++tt] = 0;
    for(int i = 1; i <= n; i++)
    {
        if(q[hh] < i - m - 1) hh++;
        f[i] = f[q[hh]] + w[i];
        while(hh <= tt && f[q[tt]] >= f[i]) tt--;
        q[++tt] = i;
    }
    
    for(int i = n - m; i <= n; i++)
    {
        if(f[i] <= t) return true;
    }
    return false;
}

int main()
{
    scanf("%d%d", &n, &t);
    for(int i = 1; i <= n; i++) scanf("%d", &w[i]);
    int l = 0, r = n;
    while(l < r)
    {
        int mid = (l + r) / 2;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    printf("%d\n", l);
    return 0;
}

3. 1087. 修剪草坪

FJ 有 $N$ 只排成一排的奶牛，编号为 $1$ 到 $N$。每只奶牛的效率是不同的，奶牛 $i$ 的效率为 $E_i$。编号相邻的奶牛们很熟悉，如果 FJ 安排超过 $K$ 只编号连续的奶牛，那么这些奶牛就会罢工去开派对。因此，现在 FJ 需要你的帮助，找到最合理的安排方案并计算 FJ 可以得到的最大效率。注意，方案需满足不能包含超过 $K$ 只编号连续的奶牛。

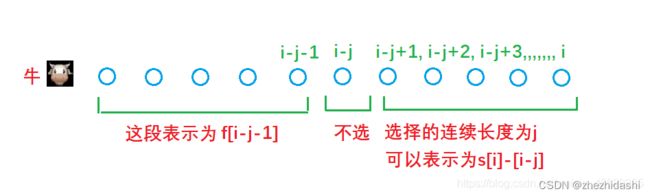
这个题有一个很简单的做法，就是类似于 烽火传递 那个题，不过我们这次是选出来不选的牛，让这些牛的效率之和最小。可以转化为在长度为 $K+1$ 的连续子序列中至少选择一个数字问最小值 $res$，所有权值之和是 $sum$，答案就是 $sum-res.$

$f(i)$：在前 $i$ 头牛里面选，方案最大值。那么不选第 $i$ 头牛的话就是 $f(i)=f(i-1)$，当然也可以选择从$i-j+1\sim i$ 头牛，且不选第 $i-j$ 头牛。就是 $f(i-j-1)+s[i]-s[i-j]$，记 $f(i-j-1)-s[i-j]=g(i-j)$，即 $g(i)=f(i-1)-s[i]$. 因此 $f(i)=\max \{f(i-1),g(i-j)+s[i]\}$. 因此我们需要找到 $\max$

#include
using namespace std;
const int N = 100010;
typedef long long ll;
ll f[N], g[N], q[N], s[N];
int n, k;
int main()
{
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; i++)
    {
        scanf("%lld", &s[i]);
        s[i] += s[i - 1];
    }

    int hh = 0, tt = -1;
    q[++tt] = 0;
    for(int i = 1; i <= n; i++)
    {
        if(q[hh] < i - k) hh++;
        f[i] = max(f[i - 1], g[q[hh]] + s[i]);
        g[i] = f[i - 1] - s[i];
        while(hh <= tt && g[q[tt]] <= g[i]) tt--;
        q[++tt] = i;
    }

    printf("%lld\n", f[n]);
    return 0;
}

4. 1091. 理想的正方形

• 题意：有一个 $a\times b$ 的整数组成的矩阵，现请你从中找出一个 $n\times n$ 的正方形区域，使得该区域所有数中的最大值和最小值的差最小。
• 二维单调队列，求方框内的最大值和最小值.

保存一个二维单调队列 $deque<int>col[M]$，记录第 $j$ 列的滑动窗口最大值；以及当前行的单调队列 $deque<int>row$，记录方框内 $col[j-k+1:j].front()$ 的最大值。每次先用 $w[i,j]$ 更新第 $j$ 列的状态（即 $col[j].back()$），再用 $col[j].front()$ 更新 $row$ 的状态.

这道题卡时间了，然后我把 O1 O2 O3 优化全开了，然后就过了.

#include
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#define x first
#define y second

using namespace std;
const int N = 1010;
typedef pair<int, int> P;
deque<int> col_max[N], col_min[N];
deque<P> row_max, row_min;
int n, m, k;
int w[N][N];
int ans = 0x3f3f3f3f;
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            scanf("%d", &w[i][j]);
        }
    }
    for(int i = 1; i <= n; i++)
    {
        row_max.clear(), row_min.clear();
        for(int j = 1; j <= m; j++)
        {
            if(col_max[j].size() && col_max[j].front() < i - k + 1) col_max[j].pop_front();
            if(col_min[j].size() && col_min[j].front() < i - k + 1) col_min[j].pop_front();
            if(row_max.size() && row_max.front().y < j - k + 1) row_max.pop_front();
            if(row_min.size() && row_min.front().y < j - k + 1) row_min.pop_front();

            while(col_max[j].size() && w[col_max[j].back()][j] <= w[i][j]) col_max[j].pop_back();
            col_max[j].push_back(i);
            while(col_min[j].size() && w[col_min[j].back()][j] >= w[i][j]) col_min[j].pop_back();
            col_min[j].push_back(i);

            while(row_max.size() && row_max.back().x <= w[col_max[j].front()][j]) row_max.pop_back();
            row_max.push_back({w[col_max[j].front()][j], j});
            while(row_min.size() && row_min.back().x >= w[col_min[j].front()][j]) row_min.pop_back();
            row_min.push_back({w[col_min[j].front()][j], j});

            if(i >= k && j >= k)
            {
                ans = min(ans, row_max.front().x - row_min.front().x);
            }
        }
    }
    printf("%d\n", ans);
}

10. 斜率优化DP（凸包优化）

1.1 301. 任务安排2

1.2 302. 任务安排3

有 $N$ 个任务排成一个序列在一台机器上等待执行，它们的顺序不得改变。机器会把这 $N$ 个任务分成若干批，每一批包含连续的若干个任务。从时刻 $0$ 开始，任务被分批加工，执行第 $i$ 个任务所需的时间是 $T_i$。另外，在每批任务开始前，机器需要 $S$ 的启动时间，故执行一批任务所需的时间是启动时间 $S$ 加上每个任务所需时间之和。一个任务执行后，将在机器中稍作等待，直至该批任务全部执行完毕。也就是说，同一批任务将在同一时刻完成。每个任务的费用是它的完成时刻乘以一个费用系数 $C_i$。请为机器规划一个分组方案，使得总费用最小。

情况一：

• $1\le n\le 5000,0\le S\le 50,1\le T_i,C_i\le 100$. 用 $O(n^2)$ 来写

设 $f(i)$ 为分配任务 $1\sim i$ 的最小花费。假设上一批最后一个任务编号是 $j$. 那么，新分配一个任务的对答案多出来的启动时间的花费是 $S\ast (sum{C}_n-sum{C}_j)$ ，任务本身的花费是 $sum{T}_i\ast (sum{C}_i-sum{C}_j)$. 即 $f(i)=\underset{0\le j<i}{\min }\{f(j)+sum{T}_i\ast (sum{C}_i-sum{C}_j)+S\ast (sum{C}_n-sum{C}_j)\}$.

#include
using namespace std;
const int N = 5010;
int f[N], sumC[N], sumT[N];
int n, S;
int main()
{
    scanf("%d%d", &n, &S);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d", &sumT[i], &sumC[i]);
        sumT[i] += sumT[i - 1], sumC[i] += sumC[i - 1];
    }
    
    memset(f, 0x3f, sizeof f);
    f[0] = 0;
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 0; j < i; j++)
        {
            f[i] = min(f[i], f[j] + sumT[i] * (sumC[i] - sumC[j]) + S * (sumC[n] - sumC[j])); 
        }
    }
    printf("%d\n", f[n]);
    return 0;
}

情况二

• $1\le n\le 3\ast 10^5,1\le T_i,C_i\le 512,0\le S\le 512$.
• 由于和 $i$ 相关的可以看作定值，和 $j$ 相关的可以看作变量。因此原等式可以这样做变化：$f(j)=(sum{T}_i+S)\ast sum{C}_j+f(i)-sum{T}_i\ast sum{C}_i-S\ast sum{C}_n$.

可以看作直线 $y=kx+b$，$y$ 是 $f(j)$，斜率是 $sum{T}_i+S$，$x$ 为 $sum{C}_j$，截距 $b$ 可以看作 $f(i)-sum{T}_i\ast sum{C}_i-S\ast sum{C}_n$ . 而 $f(j)$ 和 $sum{C}_j$ 是之前就计算出来的，目标是让 $f(i)$ 最小，就是让截距最小. 我们发现，如果把 $(sum{C}_j,f(j))$ 画在坐标系中，那么可以和答案有关的点一定是在凸包的边界上。这道题的斜率都是正数.

此题特点是斜率单调递增，横坐标也单调递增

在查询的时候，可以将队头小于当前斜率的点全部删掉；在插入的时候，将队尾所有不在凸包上的点全部删掉. 当然对于这个题横坐标 $sum{C}_i$ 本身就是单调递增的.

因此查询的点一定是一直往右走，因此查询的时候遇到斜率小与 $sum{C}_i$ 的就可以删掉了（但是要注意与上一个点的相对斜率不一定会比上一个相对斜率大）.

#include
using namespace std;
const int N = 300010;
typedef long long ll;

ll f[N], C[N], T[N], q[N], s;
int n;
int main()
{
    scanf("%d%lld", &n, &s);

    for(int i = 1; i <= n; i++)
    {
        scanf("%lld%lld", &T[i], &C[i]);
        T[i] += T[i - 1], C[i] += C[i - 1];
    }

    int hh = 0, tt = -1;
    q[++tt] = 0;

    for(int i = 1; i <= n; i++)
    {
        while(hh < tt && f[q[hh + 1]] - f[q[hh]] <= (T[i] + s) * (C[q[hh + 1]] - C[q[hh]])) hh++;
        int j = q[hh];
        f[i] = f[j] + T[i] * C[i] + s * C[n] - (T[i] + s) * C[j];
        while(hh < tt && (f[q[tt]] - f[q[tt - 1]]) * (C[i] - C[q[tt]]) >= (f[i] - f[q[tt]]) * (C[q[tt]] - C[q[tt - 1]])) tt--;
        q[++tt] = i;
    }
    printf("%lld\n", f[n]);

    return 0;
}

情况三

• $1\le n\le 3\ast 10^5,0\le S,C_i\le 512,-512\le T_i\le 512.$

• 此题特点是斜率可能不单调，但横坐标 $sum{C}_i$ 仍然是单调递增的.

• 处理方法是：在查询的时候，只能二分来找；在插入的时候，把不在凸包上的点全部删掉.

补充一句，如果横坐标不单调递增，那么需要有增添操作，那么需要用平衡树维护.

#include
using namespace std;
const int N = 300010;
typedef long long ll;
ll s, C[N], T[N], f[N];
int n, q[N];
int main()
{
    scanf("%d%lld", &n, &s);
    for(int i = 1; i <= n; i++)
    {
        scanf("%lld%lld", &T[i], &C[i]);
        T[i] += T[i - 1], C[i] += C[i - 1];
    }

    int hh = 0, tt = -1;
    q[++tt] = 0;
    for(int i = 1; i <= n; i++)
    {
        int l = hh, r = tt;
        //考虑清楚二分的边界.
        while(l < r)
        {
            int mid = (l + r) / 2;
            if((f[q[mid + 1]] - f[q[mid]]) > (__int128)(T[i] + s) * (C[q[mid + 1]] - C[q[mid]])) r = mid;
            else l = mid + 1;
        }

        int j = q[l];
        f[i] = f[j] + (__int128)T[i] * C[i] + (__int128)s * C[n] - (__int128)(T[i] + s) * C[j];
        while(hh < tt && (__int128)(f[q[tt]] - f[q[tt - 1]]) * (C[i] - C[q[tt]]) >= (__int128)(f[i] - f[q[tt]]) * (C[q[tt]] - C[q[tt - 1]])) tt--;
        q[++tt] = i;
    }
    printf("%lld\n", f[n]);
    return 0;
}

303. 运输小猫

• 小 $S$ 是农场主，他养了 $M$ 只猫，雇了 $P$ 位饲养员。农场中有一条笔直的路，路边有 $N$ 座山，从 $1$ 到 $N$ 编号。第 $i$ 座山与第 $i-1$ 座山之间的距离为 $D_i$。饲养员都住在 $1$ 号山。第 $i$ 只猫去 $H_i$ 号山玩，玩到时刻 $T_i$ 停止，然后在原地等饲养员来接。饲养员在路上行走需要时间，速度为 1 米/单位时间。你的任务是规划每个饲养员从 1 号山出发的时间，使得所有猫等待时间的总和尽量小。饲养员出发的时间可以为负。

• 设 $d$ 是前缀和，$t$ 是结束时间，那么，对于第 $i$ 只猫，只有饲养员在 $t_i-d_i$ 之后出发才能接到这只猫。因此我们设 $a_i=t_i-d_i$，那么按照 $a$ 排序，一位饲养员接一段连续子序列的小猫，那么相当于把这个子序列分为不超过 $P$ 份，每位饲养员恰好接到当前子序列的最后一只小猫. 假设饲养员是 $s_i$ 出发的，恰好接到小猫 $i$，那么小猫等待时间就是 $s_i-a_i.$

• 设 $f(j,i)$ 为第 $j$ 只饲养员接的最后一只小猫是 $i$. 上一个饲养员接的小猫是 $k$，那么 $f(j,i)=\min \{f(j-1,k)+a_i\ast (i-k)-(s_i-s_k)\}$.

$f(j-1,k)+s_k=a_i\ast k+f(j,i)-a_i\ast i+s_i$.

#include 
#include 
#include 

using namespace std;

typedef long long LL;

const int N = 100010, M = 100010, P = 110;

int n, m, p;
LL d[N], t[N], a[N], s[N];
LL f[P][M];
int q[M];

LL get_y(int k, int j)
{
    return f[j - 1][k] + s[k];
}

int main()
{
    scanf("%d%d%d", &n, &m, &p);

    for (int i = 2; i <= n; i ++ )
    {
        scanf("%lld", &d[i]);
        d[i] += d[i - 1];
    }

    for (int i = 1; i <= m; i ++ )
    {
        int h;
        scanf("%d%lld", &h, &t[i]);
        a[i] = t[i] - d[h];
    }

    sort(a + 1, a + m + 1);

    for (int i = 1; i <= m; i ++ ) s[i] = s[i - 1] + a[i];

    memset(f, 0x3f, sizeof f);
    for (int i = 0; i <= p; i ++ ) f[i][0] = 0;

    for (int j = 1; j <= p; j ++ )
    {
        int hh = 0, tt = 0;
        q[0] = 0;

        for (int i = 1; i <= m; i ++ )
        {
            while (hh < tt && (get_y(q[hh + 1], j) - get_y(q[hh], j)) <= a[i] * (q[hh + 1] - q[hh])) hh ++ ;
            int k = q[hh];
            f[j][i] = f[j - 1][k] - a[i] * k + s[k] + a[i] * i - s[i];
            while (hh < tt && (get_y(q[tt], j) - get_y(q[tt - 1], j)) * (i - q[tt]) >=
                (get_y(i, j) - get_y(q[tt], j)) * (q[tt] - q[tt - 1])) tt -- ;
            q[ ++ tt] = i;
        }
    }

    printf("%lld\n", f[p][m]);

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/128992/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

11. 基环树DP

359. 创世纪

12. 四边形不等式DP

13. 插头DP

14. 环形与后效性处理

15. 倍增优化 DP

16. 数据结构优化 DP