莫顿曲线映射 二维到一维的变换 MD（莫顿）码 正向变换 线性四叉树

线性四叉树

（Linear Quadtree）是一种基于莫顿码（Morton Code）的数据结构，用于存储和处理二维空间中的信息。

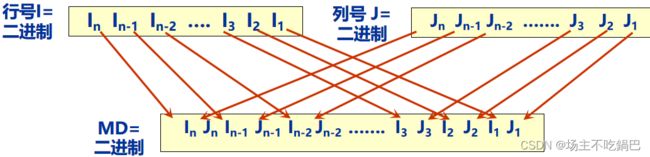
莫顿码是一种将二维坐标映射为一维编码的方法，它将一个二维点的坐标表示为一个整数，使得相邻的二维点在一维空间中的编码也相邻。莫顿码通常用于空间索引和空间分区等应用中。

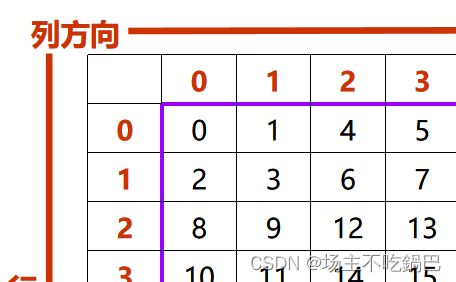
线性四叉树是基于莫顿码的一种四叉树实现方式，它将二维空间划分为一系列正方形区域，并将每个区域标记为叶子节点。每个叶子节点对应着一个莫顿码，通过莫顿码的前缀匹配可以快速定位到对应的叶子节点。线性四叉树的节点可以压缩为一个连续的数组，因此可以实现高效的存储和访问。

线性四叉树常用于地理信息系统（GIS）和计算机图形学等领域中，用于表示地图、图像和空间数据等信息。它具有高效的空间索引和查询能力，可以快速地进行空间范围查询、最近邻查询和空间聚类等操作。

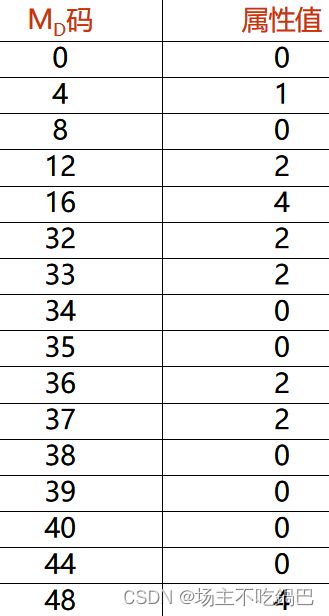
线性四叉树则只存贮最后叶结点的信息，包括叶结点的位置编码/地址码、属性或灰度值

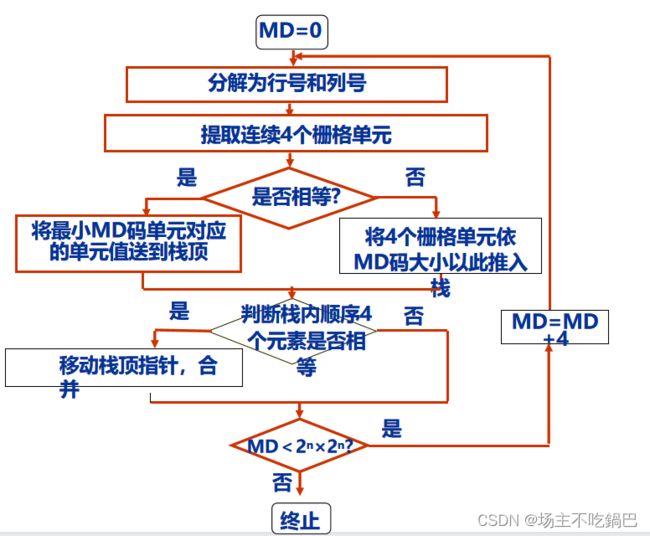
 线性四叉树 二维到一维 的变换的具体算法：

 

函数和结构体的定义 :

#include 
#include 

#define N 8
#define MAXSIZE 100

typedef struct          //栈的存储结构
{
    int data[MAXSIZE];
    int MD[MAXSIZE];
    int top;
}stack1;

void stackinitiate(stack1 *s);    //初始化栈
int getlines(int md);			//由MD码二进制计算行
int getrow(int md);		    	//由MD码二进制计算列
int getbinary(int md);          //获得MD码的二进制
void push (stack1 *q,int e,int n);     //入栈
void pri(stack1 q);                   //打印栈
void pop(stack1 *q,int i);          //出栈

函数的具体实现:

int getline(int md)                  //由二进制MD码，获得对应行
{
	int res=0;
	int i=0;
	while(md){
		md/=10;
		res+=md%10*pow(2,i++);
		md/=10;
	}
	return res;
}

int getrow(int md)                   //由二进制MD码，获得对应列
{
	int res=0;
	int i=0;
	while(md){
		res+=md%10*pow(2,i++);
		md/=100;
	}
	return res;
}

int getbinary(int md)            //由十进制MD码，获得二进制MD码
{
	double res=0;
	int i=0;
	while(md){
		int temp=md%2;
		res+=temp*pow(10,i++);
		md=md/2;
	}
	return res;
}


void push (stack1 *s,int e,int n)   //入栈
{
	
	s->data[s->top]=n;
	s->MD[s->top]=e;
	s->top++;
}

void pri(stack1 q)                     //从栈底打印整个栈
{
	for(int i=0;i!=q.top;i++){
		printf("%d,%d\n",q.MD[i],q.data[i]);
	}
}

void stackinitiate(stack1 *s)            //初始化栈
{
	s->top=0;
}

void pop(stack1 *q,int i){                 //出栈i个元素
	q->top-=i;
}

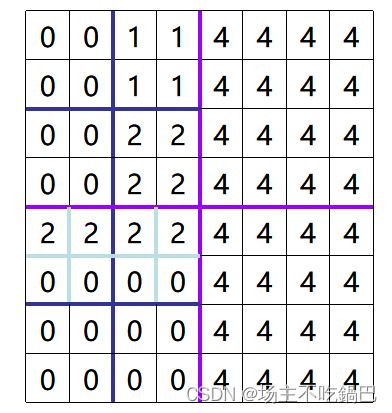
将二维的网格导填入到二维数组中，并初始化栈

int s[N][N]={                     //将PPT内的数据填入二维数组中
		{0,0,1,1,4,4,4,4},
		{0,0,1,1,4,4,4,4},
		{0,0,2,2,4,4,4,4},
		{0,0,2,2,4,4,4,4},
		{2,2,2,2,4,4,4,4},
		{0,0,0,0,4,4,4,4},
		{0,0,0,0,4,4,4,4},
		{0,0,0,0,4,4,4,4},
	};

	stack1 a;                              //创建栈  
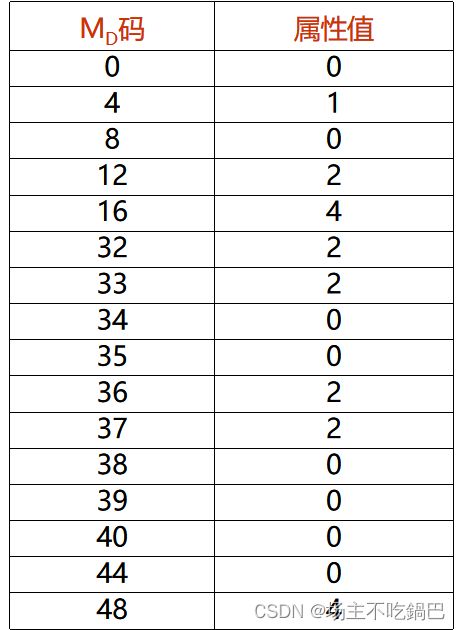
	stackinitiate(&a);                     //初始化

按算法结果应该为这样：

核心算法：

int md=0;
	while(md3){                              //判断栈顶四个元素是否相等
			int h=a.top-1;
			if(a.data[h]==a.data[h-1]&&a.data[h]==a.data[h-2]&&a.data[h]==a.data[h-3]){		
			   pop(&a,3);          //最上面三个元素出栈
		    }
		}
		md+=4;
	}
	pri(a);                //打印
	return 0;
}

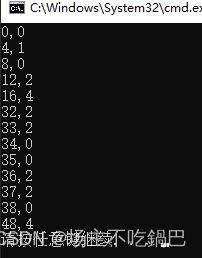
 打印结果:

结果一致，证明没有问题

 关于中间的函数实现，我采用了比较愚蠢的方法，下面我搜集了各类资料，展示使用位运算的实现

十进制MD码 转化为 二进制MD码

uint32_t decimal_to_binary(uint32_t md) {
    uint32_t binary = 0;
    uint32_t bit = 1;
    while (md > 0) {
        if (md & 1) {
            binary += bit;
        }
        bit <<= 1;  // 左移一位，相当于乘以2
        md >>= 1;   // 右移一位，相当于除以2
    }
    return binary;
}

• 首先判断 md 的最后一位是否为1，如果是，就在二进制数的对应位上加上当前位的权值 bit。
• 然后将 bit 左移一位，相当于将当前位的权值乘以2。
• 接着将 md 右移一位，相当于将当前位去掉，准备处理下一位。

二进制MD码转 行列号（这里的行为偶数，奇数为列）

#include 

void getRowColumn(int md, int level) {
    int row = 0;
    int col = 0;

    for (int i = 1; i <= level/2 +1; i++) {
        row |= (md & (1 << (2 * i -1))) >> i;
        col |= (md & (1 << (2 * i -2))) >> i-1;
    }

    printf("Row: %d, Column: %d\n", row, col);
}

int main() {
    int md = 0b100;  // 二进制的MD码
    int level = 3;   // 二进制码的长度

    getRowColumn(md, level);
	
    return 0;
}