集成学习方法：bagging、boosting和stacking

「团结就是力量」。这句老话很好地表达了机器学习领域中强大「集成方法」的基本思想。总的来说，许多机器学习竞赛（包括 Kaggle）中最优秀的解决方案所采用的集成方法都建立在一个这样的假设上：将多个模型组合在一起通常可以产生更强大的模型。

  本文将讨论一些众所周知的概念，如自助法、装袋（bagging）、随机森林、提升法（boosting）、堆叠法（stacking）以及许多其它的基础集成学习模型。

  为了使所有这些方法之间的联系尽可能清晰，我们将尝试在一个更广阔和逻辑性更强的框架中呈现它们，希望这样会便于读者理解和记忆。

何为集成方法？

  集成学习是一种机器学习范式。在集成学习中，我们会训练多个模型（通常称为「弱学习器」）解决相同的问题，并将它们结合起来以获得更好的结果。最重要的假设是：当弱模型被正确组合时，我们可以得到更精确和/或更鲁棒的模型。

单一弱学习器

  在机器学习中，无论是面临分类问题还是回归问题，模型的选择对于获得好的结果都是非常重要的。这种选择取决于问题的许多变量: 数据的数量、空间的维数、分布假设…

  低偏差和低方差，尽管它们经常在相反的方向上变化，是模型最基本的两个特征。实际上，为了能够“解决”一个问题，我们希望我们的模型有足够的自由度来解决我们正在处理的数据的基本复杂性，但我们也希望它没有太多的自由度，以避免高变化，使模型保持健壮。这是众所周知的偏差-方差折衷。

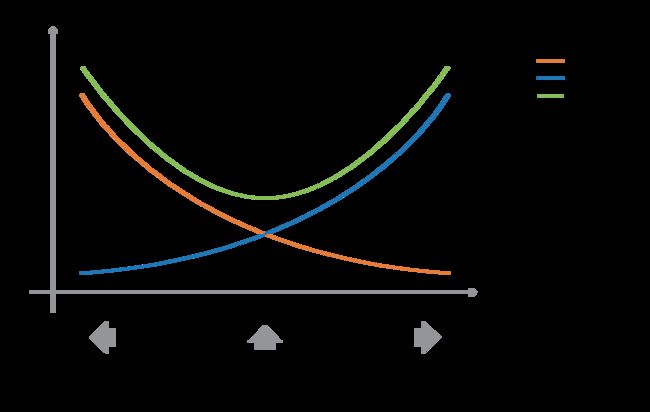
  在集成学习理论中，我们称弱学习器(或基础模型)为模型，这些模型可以用作构建模块，通过组合几个模型来设计更复杂的模型。大多数情况下，这些基本模型本身的表现并不好，要么是因为它们有很高的偏差(例如，低自由度模型) ，要么是因为它们有太多的“变化”，以至于不够健壮(例如，高自由度模型)。然后，集成方法的思想是尝试通过将这些弱学习者中的若干个学习者结合在一起来减少这些弱学习者的偏差和/或方差，从而创建一个强学习器(或集成模型) ，以获得更好的表现。

组合弱学习器

  为了建立一个集成学习方法，我们首先要选择待聚合的基础模型。在大多数情况下（包括在众所周知的 bagging 和 boosting 方法中），我们会使用单一的基础学习算法，这样一来我们就有了以不同方式训练的同质弱学习器。这样得到的集成模型被称为「同质的」。然而，也有一些方法使用不同种类的基础学习算法：将一些异质的弱学习器组合成「异质集成模型」。

  很重要的一点是：我们对弱学习器的选择应该和我们聚合这些模型的方式相一致。如果我们选择具有低偏置高方差的基础模型，我们应该使用一种倾向于减小方差的聚合方法；而如果我们选择具有低方差高偏置的基础模型，我们应该使用一种倾向于减小偏置的聚合方法。

  这就引出了如何组合这些模型的问题。我们可以用三种主要的旨在组合弱学习器的「元算法」：

• bagging，该方法通常考虑的是同质弱学习器，相互独立地并行学习这些弱学习器，并按照某种确定性的平均过程将它们组合起来。
• boosting，该方法通常考虑的也是同质弱学习器。它以一种高度自适应的方法顺序地学习这些弱学习器（每个基础模型都依赖于前面的基础模型），并按照某种确定性的策略将它们组合起来。
• stacking，该方法通常考虑的是异质弱学习器，并行地学习它们，并通过训练一个「元模型」将它们组合起来，根据不同弱模型的预测结果输出一个最终的预测结果。

  非常粗略地说，我们可以说 bagging 的重点在于获得一个方差比其组成部分更小的集成模型，而 boosting 和 stacking 则将主要生成偏差比其组成部分更低的集成模型（即使方差也可以被减小）。

  在接下来的章节中，我们将具体介绍 bagging 和 boosting 方法（它们比 stacking 方法使用更广泛，并且让我们可以讨论一些集成学习的关键概念），然后简要概述 stacking 方法。

  我们可以将弱学习器结合起来以得到性能更好的模型。组合基础模型的方法应该与这些模型的类型相适应。

关于装袋（Bagging）

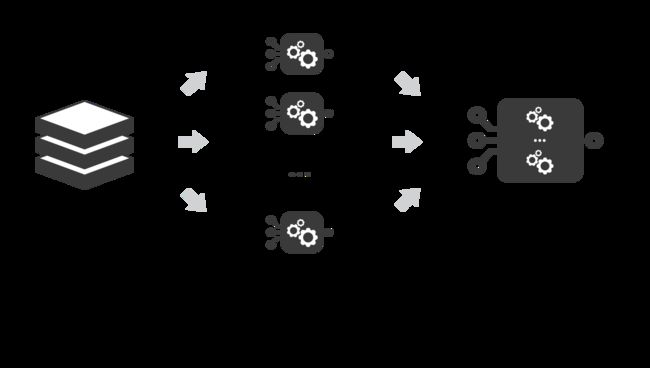
  在「并行化的方法」中，我们单独拟合不同的学习器，因此可以同时训练它们。最著名的方法是装袋（Bagging），它的目标是生成比单个模型更鲁棒（方差小）的集成模型。

自助法（Bootstrapping）

  这种统计技术先随机抽取出作为替代的 B 个观测值，然后根据一个规模为 N 的初始数据集生成大小为 B 的样本（称为自助样本）。

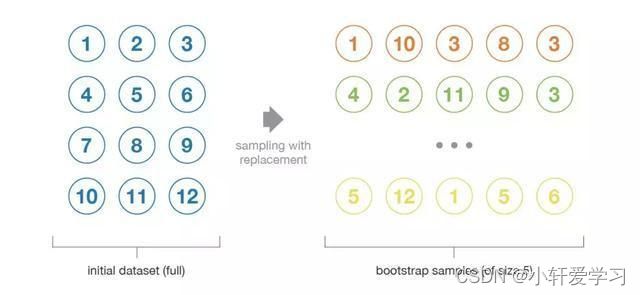
  在某些假设条件下，这些样本具有非常好的统计特性：在一级近似中，它们可以被视为是直接从真实的底层（并且往往是未知的）数据分布中抽取出来的，并且彼此之间相互独立。因此，它们被认为是真实数据分布的代表性和独立样本（几乎是独立同分布的样本）。

  为了使这种近似成立，必须验证两个方面的假设。

  首先初始数据集的大小 N 应该足够大，以捕获底层分布的大部分复杂性。这样，从数据集中抽样就是从真实分布中抽样的良好近似（代表性）。

  其次，与自助样本的大小 B 相比，数据集的规模 N 应该足够大，这样样本之间就不会有太大的相关性（独立性）。注意，接下来我们可能还会提到自助样本的这些特性（代表性和独立性），但读者应该始终牢记：「这只是一种近似」。

  举例而言，自助样本通常用于评估统计估计量的方差或置信区间。根据定义，统计估计量是某些观测值的函数。因此，随机变量的方差是根据这些观测值计算得到的。

  为了评估这种估计量的方差，我们需要对从感兴趣分布中抽取出来的几个独立样本进行估计。在大多数情况下，相较于实际可用的数据量来说，考虑真正独立的样本所需要的数据量可能太大了。

  然而，我们可以使用自助法生成一些自助样本，它们可被视为「最具代表性」以及「最具独立性」（几乎是独立同分布的样本）的样本。这些自助样本使我们可以通过估计每个样本的值，近似得到估计量的方差。

自助法经常被用于评估某些统计估计量的方差或置信区间。

装袋（Bagging）

  当训练一个模型时，无论是处理分类问题还是回归问题，我们都会得到一个接受输入，返回输出的函数，这个函数是针对训练数据集定义的。由于训练数据集的理论方差（我们提醒数据集是一个来自真实的未知潜在分布的观测样本），拟合模型也受到变异性的影响: 如果另一个数据集被观测到，我们会得到一个不同的模型。

  装袋的想法很简单: 我们要拟合几个独立的模型，并“平均”他们的预测，以获得一个有较低方差的模型。然而在实践中，我们不能拟合完全独立的模型，因为这需要太多的数据。因此，我们依赖于自助法中的“近似性质”(代表性和独立性)来拟合几乎独立的模型。

  首先，我们通过自助法创建多个样本，使每个样本作为一个(几乎)独立的数据集（来自真正的分布）。然后，我们可以使用多个弱学习器来拟合这些样本，并最终聚合他们。这样我们就可以“平均”他们的输出。这样就可以得到一个比基础模型有更小方差的集成模型。粗略地说，由于样本是近似的独立同分布(i.i.d.) ，因此基础模型也是近似的。然后，“平均”弱学习器输出不改变期望，但减小其方差(就像平均 i.i.d. 随机变量保持期望值，但减小方差)。

  因此，假设我们有 L个大小为B 的样本(L个独立数据集)

  我们可以拟合 L个几乎独立的弱学习者(每个数据集一个)

  然后将它们聚合成某种平均过程，得到方差较小的集成模型。例如，我们可以定义我们的强模型

  有几种可能的方法来聚合多个模型。对于回归问题，单个模型的输出可以按字面意义取平均值以获得集合模型的输出。对于分类问题，每个模型输出的类可视为一个表决，得到多数表决票的类由集合模型返回(称为硬表决)。对于分类问题，我们还可以考虑所有模型返回的每个类的概率，对这些概率进行平均，并返回最高的平均概率类(这称为软投票)。如果可以使用任何相关的权重，平均数或投票数可以是简单的或加权的（如果存在，可以给单个模型的输出加权重）。

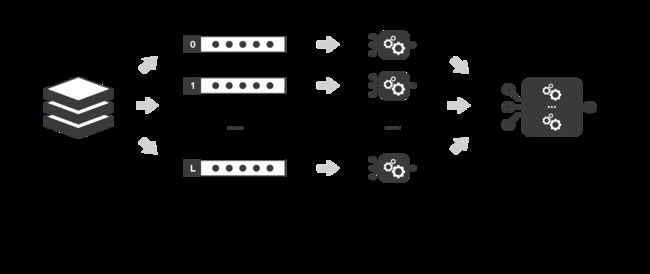
  最后，我们可以提到 bagging 最大的优点之一是它可以被并行化。由于不同的模型是相互独立的，因此可以根据需要使用密集的并行处理技术。

随机森林（Random forests）

  学习树是集成学习方法中非常流行的基本模型。由多棵树组成的强大的学习器可以称为“森林”。组成森林的树木可以选择浅(深度)或深(深度)树。浅树方差较小，但偏差较大，因此对于我们将在后面描述的序列化的方法来说，它将是更好的选择。另一方面，深层树种偏差小，但方差大，因此，对于以减少方差为主的装袋（Bagging）方法是较好的选择。

  随机森林方法是一种装袋方法，其中深树通过拟合自助法产生的样本，然后结合起来产生一个低方差的输出。然而，随机森林还使用了另一个技巧来使多个拟合树之间的相关性降低一点: 当生长每一棵树时，我们不再仅仅在数据集中的观察值上进行抽样来生成一个样本，我们也对特征进行抽样，并且只保留其中的一个随机特征子集来构建树。

  对特征进行抽样确实会产生这样的效果，即所有的树都不会查看完全相同的信息来做出决策，因此，它降低了不同树的返回输出之间的相关性。除了特征抽样，另一个优点是它使决策过程对缺失数据更加健壮: 有缺失数据的观测(不管是否来自训练数据集)仍然可以根据树进行回归或分类，这些树只考虑没有缺失数据的特征。因此，随机森林算法结合了装袋和随机特征子空间选择的概念，以创建更健壮的模型。

关于提升（Boosting）

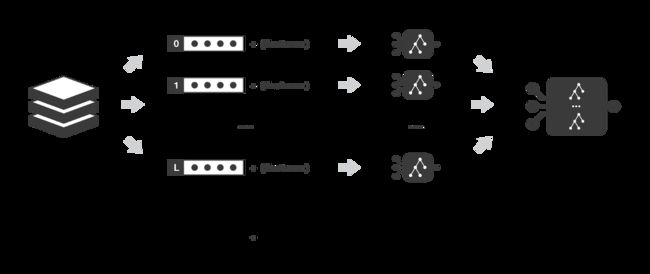
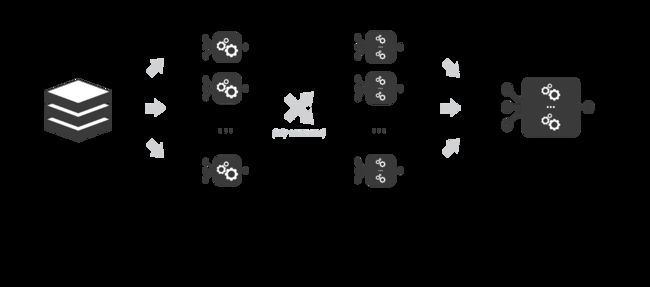
  在序列方法中，不同的组合弱模型不再相互独立地进行拟合。其思想是迭代拟合模型，使模型在给定步骤的训练中取决于在前面步骤中拟合的模型。“ Boosting”是这些方法中最著名的一种，它产生的集成模型通常比组成该模型的弱学习器有更小的偏差。

  Boosting 方法和Bagging 方法的工作思路是一样的：我们构建一系列模型，将它们聚合起来得到一个性能更好的强学习器。然而，与重点在于减小方差的 bagging 不同，boosting 着眼于以一种适应性很强的方式顺序拟合多个弱学习器：序列中每个模型在拟合的过程中，会更加重视那些序列中之前的模型处理地很糟糕的观测数据。

  直观地说，每个模型都把注意力集中在目前最难拟合的观测数据上。这样一来，在这个过程的最后，我们就获得了一个具有较低偏置的强学习器（我们会注意到，Boosting 也有减小方差的效果）。和Bagging 一样，Boosting 也可以用于回归和分类问题。

  由于其重点在于减小偏差，用于 Boosting 的基础模型通常是那些低方差高偏差的模型。例如，如果想要使用树作为基础模型，我们将主要选择只有少许几层的较浅决策树。而选择低方差高偏差模型作为 Boosting 弱学习器的另一个重要原因是：这些模型拟合的计算开销较低（参数化时自由度较低）。

  实际上，由于拟合不同模型的计算无法并行处理（与 Bagging 不同），顺序地拟合若干复杂模型会导致计算开销变得非常高。一旦选定了弱学习器，我们仍需要定义它们的拟合方式（在拟合当前模型时，要考虑之前模型的哪些信息？）和聚合方式（如何将当前的模型聚合到之前的模型中？）在接下来的两小节中，我们将讨论这些问题，尤其是介绍两个重要的 Boosting 算法：自适应提升（adaboost ）和梯度提升（gradient boosting）。

  简而言之，这两种元算法在顺序化的过程中创建和聚合弱学习器的方式存在差异。自适应增强算法会更新附加给每个训练数据集中观测数据的权重，而梯度提升算法则会更新这些观测数据的值。这里产生差异的主要原因是：两种算法解决优化问题（寻找最佳模型——弱学习器的加权和）的方式不同。

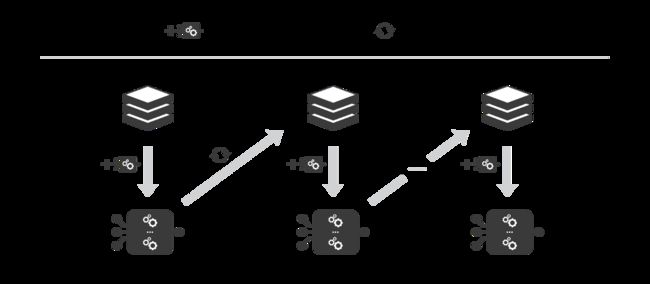
自适应 （boosting）

  在自适应 boosting（通常被称为「adaboost」）中，我们将集成模型定义为 L 个弱学习器的加权和。

  寻找这种最佳集成模型是一个「困难的优化问题」。因此，我们并没打算一次性地解决该问题（找到给出最佳整体加法模型的所有系数和弱学习器），而是使用了一种更易于处理的「迭代优化过程」（即使它有可能导致我们得到次优解）。另外，我们将弱学习器逐个添加到当前的集成模型中，在每次迭代中寻找可能的最佳组合（系数、弱学习器）。换句话说，我们循环地将 s_l 定义如下：

  其中，c_l 和 w_l 被挑选出来，使得 s_l 是最适合训练数据的模型，因此这是对 s_(l-1) 的最佳可能改进。我们可以进一步将其表示为：

  其中，E(.) 是给定模型的拟合误差，e(.,.)是损失/误差函数。因此，我们并没有在求和过程中对所有 L 个模型进行「全局优化」，而是通过「局部」优化来近似最优解并将弱学习器逐个添加到强模型中。

  更特别的是，在考虑二分类问题时，我们可以将 adaboost 算法重新写入以下过程：首先，它将更新数据集中观测数据的权重，训练一个新的弱学习器，该学习器重点关注当前集成模型误分类的观测数据。其次，它会根据一个表示该弱模型性能的更新系数，将弱学习器添加到加权和中：弱学习器的性能越好，它对强学习器的贡献就越大。

  因此，假设我们面对的是一个二分类问题：数据集中有 N 个观测数据，我们想在给定一组弱模型的情况下使用 adaboost 算法。在算法的起始阶段（序列中的第一个模型），所有的观测数据都拥有相同的权重「1/N」。然后，我们将下面的步骤重复 L 次（作用于序列中的 L 个学习器）：

• 用当前观测数据的权重拟合可能的最佳弱模型
• 计算更新系数的值，更新系数是弱学习器的某种标量化评估指标，它表示相对集成模型来说，该弱学习器的分量如何
• 通过添加新的弱学习器与其更新系数的乘积来更新强学习器
• 计算新观测数据的权重，该权重表示我们想在下一轮迭代中关注哪些观测数据（聚和模型预测错误的观测数据的权重增加，而正确预测的观测数据的权重减小）

  重复这些步骤，我们顺序地构建出 L 个模型，并将它们聚合成一个简单的线性组合，然后由表示每个学习器性能的系数加权。注意，初始 adaboost 算法有一些变体，比如 LogitBoost（分类）或 L2Boost（回归），它们的差异主要取决于损失函数的选择。

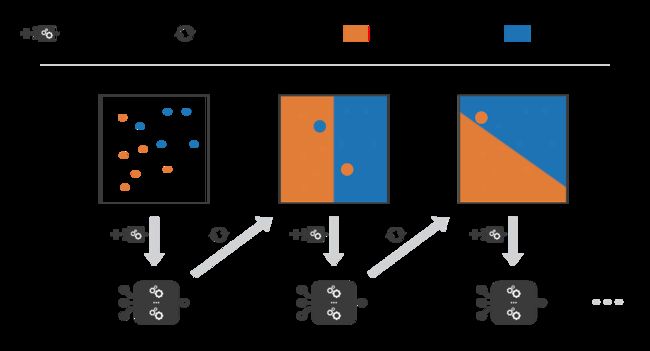
  Adaboost 在每次迭代中更新观测数据的权重。正确分类的观测数据的权重相对于错误分类的观测数据的权重有所下降。在最终的集成模型中，性能更好的模型具有更高的权重。

Gradient boosting

  在梯度提升算法中，我们尝试建立的集合模型也是弱学习器的加权和。

  正如我们在 adaboost 中提到的，在这种形式下找到最优模型太困难了，需要迭代方法。与适应性增强的主要区别在于顺序优化过程的定义。事实上，梯度提升（Gradient boosting）把这个问题归结为一个梯度下降法的问题: 在每次迭代中，我们用一个弱学习器去拟合当前集合模型中拟合误差梯度的负值。让我们来澄清最后一点。首先，可以写出梯度下降法模型上的理论过程：

其中 E (.)是给定模型的拟合误差，c_l 是对应于步长的系数

是 总体模型的l-1步的拟合误差梯度的相反数。

  这个(相当抽象的)与梯度相反的函数，在实践中，只能对训练数据集中的观测值进行评估(我们知道这些观测值的输入和输出) : 这些评估值被称为附加到每个观测值的伪残差。此外，即使我们知道这些伪残差的值，我们也不想在集成模型中添加任何类型的函数: 我们只想添加一个新的弱模型实例。因此，自然而然的事情就是将一个弱学习器与为每个观察计算的伪残差相匹配。最后，通过一维优化过程计算系数 c_l(线性搜索以获得最佳步长)。

  因此，假设我们想要对给定的一系列弱模型使用梯度提升技术。在算法的最初(序列的第一个模型) ，伪残差被设置为等于观测值。然后，我们重复 L 次(对于序列的L模型)以下步骤:

• 拟合一个弱学习器到伪残差(朝当前强学习器的近似相反的梯度方向)

• 计算最佳步长的值，该值通过我们在新的弱学习器的方向上更新集成模型的多少来定义

• 通过添加新的弱学习器乘以步长来更新集成模型(按梯度下降法的步长)

• 计算新的伪残差，这表明，对于每个观测，我们下一步要更新的集合模型预测的方向

  重复这些步骤，然后我们按顺序构建L模型，并按照梯度下降法方法将它们聚合起来。请注意，当Adaboost试图在每次迭代中精确地解决“本地”优化问题(找到最好的弱学习器及其系数添加到强模型中)时，Gradient boosting使用的是梯度下降法方法，可以更容易地适应大量的损失函数。因此，梯度提升可以被认为是 adaboost 到任意可微损失函数的推广。

关于Stacking

  Stacking 与 bagging 和 boosting 主要存在两方面的差异。首先，Stacking 通常考虑的是异质弱学习器（不同的学习算法被组合在一起），而bagging 和 boosting 主要考虑的是同质弱学习器。其次，stacking 学习用元模型组合基础模型，而bagging 和 boosting 则根据确定性算法组合弱学习器。

堆叠法（Stacking）

  正如上文已经提到的，stacking 的概念是学习几个不同的弱学习器，并通过训练一个元模型来组合它们，然后基于这些弱模型返回的多个预测结果输出最终的预测结果。因此，为了构建 stacking 模型，我们需要定义两个东西：想要拟合的 L 个学习器以及组合它们的元模型。
  例如，对于分类问题来说，我们可以选择 KNN 分类器、logistic 回归和SVM 作为弱学习器，并决定学习神经网络作为元模型。然后，神经网络将会把三个弱学习器的输出作为输入，并返回基于该输入的最终预测。
  所以，假设我们想要拟合由 L 个弱学习器组成的 stacking 集成模型。我们必须遵循以下步骤：

• 将训练数据分为两组
• 选择 L 个弱学习器，用它们拟合第一组数据
• 使 L 个学习器中的每个学习器对第二组数据中的观测数据进行预测
• 在第二组数据上拟合元模型，使用弱学习器做出的预测作为输入

  在前面的步骤中，我们将数据集一分为二，因为对用于训练弱学习器的数据的预测与元模型的训练不相关。因此，将数据集分成两部分的一个明显缺点是，我们只有一半的数据用于训练基础模型，另一半数据用于训练元模型。

  为了克服这种限制，我们可以使用某种「k-折交叉训练」方法（类似于 k-折交叉验证中的做法）。这样所有的观测数据都可以用来训练元模型：对于任意的观测数据，弱学习器的预测都是通过在 k-1 折数据（不包含已考虑的观测数据）上训练这些弱学习器的实例来完成的。

  换句话说，它会在 k-1 折数据上进行训练，从而对剩下的一折数据进行预测。迭代地重复这个过程，就可以得到对任何一折观测数据的预测结果。这样一来，我们就可以为数据集中的每个观测数据生成相关的预测，然后使用所有这些预测结果训练元模型。

多层堆叠法（Multi-levels Stacking）
  堆叠的一个可能的延伸是多层堆叠。作为一个例子，让我们考虑一个三层叠加。在第一个层次(第一层) ，我们拟合的 L个弱学习器。然后，在第二个层次上，我们拟合M个这样的元模型，而不是用单一的元模型对弱模型的预测(正如它在前面的小节中所描述的)。最后，在第三个层次，我们拟合最后一个元模型，它将前一个层次中的M个元模型的返回作为输入进行预测。
  从实用的角度来看，需要注意对于一个多层次堆叠集成模型的不同层次中的元模型来说，我们几乎可以选择任意的我们想要的学习算法(甚至算法已经在较低层次上使用)。我们还可以增加层次，当然这可能会造成很大的数据开销(如果不使用类似 k-folds 的技术，那么就需要更多的数据) ，或者造成时间开销(如果使用类似 k-folds 的技术，那么就需要更多模型)。

  最后，我们想通过提醒来结束本文，集成学习是关于组合一些基本模型，以获得一个具有更好的性能/属性的集成模型。因此，即使装袋、增强和堆叠是最常用的集成方法，变体也是可能的，可以设计成更好地适应某些具体问题。这主要需要两件事: 充分理解我们所面临的问题… … 并且要有创造力！