Python时间序列分析详细实例（附代码）

目录

一、时间序列模型简介

二、案例分析

三、模型构建 

四、结果分析

---

一、时间序列模型简介

    正常的数据类型分为三种：横截面数据、时间序列数据和面板数据三类。其中，时间序列是按照一定的时间间隔排列的一组数据，其时间间隔可以是任意的时间单位，如小时、日、周月等。在本例中为每天某产品的需求量，这些数据形成了以一定时间间隔的数据。

时间序列数据包含时间要素和数值要素，通过对这些时间序列的分析，从中发现和揭示现象发展变化的规律，并将这些知识和信息用于预测。比如需求量是上升还是下降，是否与季节有关，是否可以通过现有的数据预测未来的需求量是多少等。其变化规律有：长期趋势、季节趋势、循环变动和不规则变动四种。

采用时间序列分析进行预测时需要一系列的模型，这种模型称为时间序列模型。

#导入库
import numpy as np
import pandas as pd 
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.keras import layers,Input,optimizers
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_absolute_percentage_error
from statsmodels.graphics.tsaplots import plot_acf
from sklearn.model_selection import train_test_split
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.tsa.stattools import adfuller
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.graphics.api import qqplot

二、案例分析

判断该时间序列的特征可以帮助我们理解数据并且选择合适的模型
在做时间序列分析时，我们需要对时间序列进行平稳性检验。我们这里讨论的主要是序列的弱平稳性，因为在实际应用中我们很难获得随机序列的分布函数，所有严平稳的使用较少。弱平稳即时间序列的均值为常数且其方差是只和时间间隔有关的一元函数。其意义在于其分析遵循数理统计学的基本原理，都是利用样本信息来推测总体信息。而由弱平稳性的特点可以加大减少了随机变量的个数，并且增加了待估参数的样本量，从而降低了时序分析的难度。
平稳性检验的方法主要有：时序图检验、自相关图检验和构造统计量检验
结果分析：我们主要聚焦acf图的分析。平稳序列通常具有短期相关性，即随着延迟期数k的增加，平稳序列的自相关系数会很快地衰减为零。acf法是直接通过假设检验的方法来验证平稳性。adf是一种单位根检验方法。
                                                H0：具有单位根，属于非平稳序列
                                                H1：没有单位根，属于平稳序列

##从文件中读取数据
data_total=pd.read_excel('物料需求量表 按周求和(1)(1）.xlsx')

##刻画数据的几项主要特征
print(data_total.head())
print(data_total.info())
print(data_total.describe())
(data_total[data_total.isnull()]==True).count()

##接下来我们将以物料编码为6004020656的需求量为例展开分析
data_0656=data_total[data_total['物料编码']==6004020656]
X_0656=data_0656['日期']
Y_0656=data_0656['需求量']
data["diff1"]=Y_0656.diff(1).dropna()
data["diff2"]=Y_0656.diff(2).dropna()
data1=data.append(Y_0656)
data1.plot(subplots=True,figsize=(18,12),title='0656的差分图')
X_0656.head()
plt.scatter(X_0656,Y_0656)
plt.xlabel("data")
plt.ylabel("demand_0656")
Y=Y_0656-Y_0656.mean()
plot_acf(Y_0656)

demand_result = adfuller(Y_0656)
print("The ADF Statistic of demand yield:%f"%demand_result[0])
print("The p value of demand yield:%f"%demand_result[1])

结果分析：在该例中，需求量的adf值为-7.906830，理论上adf值越负说明越能拒绝原假设，同时p值为0.0000说明拒绝原假设，该序列是一个平稳序列。从自相关函数图中可以观察到比较明显的拖尾性

三、模型构建 

接下来我们主要利用Python中的StandardScaler库对数据进行训练集和测试集的划分
并且可视化

dataset=Y_0656.values
st=StandardScaler()
dataset_st=st.fit_transform(dataset.reshape(-1,1))
print("standarize",dataset_st)
plt.figure(figsize=(12,8))
plt.scatter(X_0656,Y_0656)
plt.xlabel("data")
plt.ylabel("demand_0656")
train_size=int(len(dataset_st)*0.7)
test_size=len(dataset_st)-train_size
train,test=dataset_st[0:train_size],dataset_st[train_size:len(dataset_st)]
print(len(train))
print(len(test))

由于时间序列主要具有短期相关性，所以我们可以设置回测的天数为2，即用昨天和前天的数据来预测明天的需求量

def data_set(dataset,lookback):
    dataX,dataY=[],[]
    for i in range (len(dataset)-lookback-1):
        a=dataset[i:(i+lookback)]
        dataX.append(a)
        dataY.append(dataset[i+lookback])
    return np.array(dataX),np.array(dataY)

lookback=2
trainX,trainY=data_set(train,lookback)
testX,testY=data_set(test,lookback)
print('trainX:',trainX.shape,trainY.shape)
print(trainX)

接下来我们设计神经网络结构

input_shape=Input(shape=(trainX.shape[1],trainX.shape[2]))
lstm1=layers.LSTM(32,return_sequences=1)(input_shape)
print("lstm1:",lstm1.shape)
lstm2=layers.LSTM(64,return_sequences=0)(lstm1)
print("lstm2:",lstm2.shape)
dense1=layers.Dense(64,activation="relu")(lstm2)
print("dense:",dense1.shape)
dropout=layers.Dropout(rate=0.2)(dense1)
print("dropout:",dropout.shape)
output_shape=layers.Dense(1,activation="relu")(dropout)
lstm_model=tf.keras.Model(input_shape,output_shape)
lstm_model.compile(loss="mean_squared_error",optimizer="Adam",metrics=["mse"])
history=lstm_model.fit(trainX,trainY,batch_size=16,epochs=10,validation_split=0.1,verbose=1)

>>结果
lstm_model.summary()

 Layer (type)                Output Shape              Param #   
=================================================================
 input_2 (InputLayer)        [(None, 2, 1)]            0         
                                                                 
 lstm_2 (LSTM)               (None, 2, 32)             4352      
                                                                 
 lstm_3 (LSTM)               (None, 64)                24832     
                                                                 
 dense_2 (Dense)             (None, 64)                4160      
                                                                 
 dropout_1 (Dropout)         (None, 64)                0         
                                                                 
 dense_3 (Dense)             (None, 1)                 65        
                                                                 
=================================================================
Total params: 33,409
Trainable params: 33,409
Non-trainable params: 0
_________________________________________________________________

模型预测

predict_trainY=lstm_model.predict(trainX)
predict_testY=lstm_model.predict(testX)
testY_real=st.inverse_transform(testY)
testY_predict=st.inverse_transform(predict_testY)
print("Y for test:",testY_predict,testY_predict.shape)
print("Y for real:",testY_real,testY_real.shape)
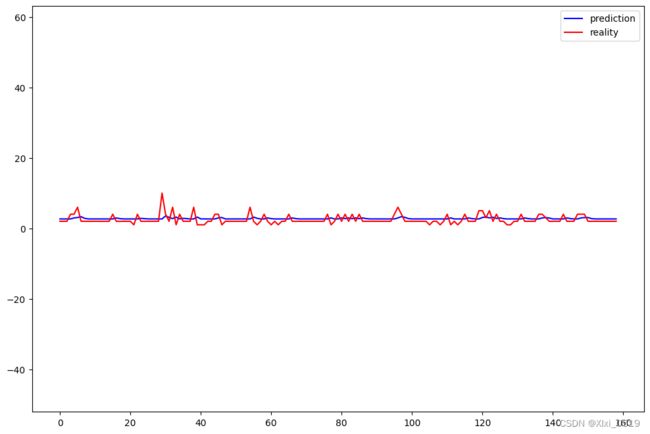
plt.figure(figsize=(12,8))
plt.plot(testY_predict,"b",label="prediction")
plt.plot(testY_real,"r",label="reality")
plt.legend()
plt.axis('equal')
plt.show()
print('回归模型平均绝对百分比误差：',mean_absolute_percentage_error(testY_real,testY_predict))

四、结果分析

从图像上来说预测值和真实值的差别不大，同时我们利用平均绝对误差来衡量模型的好坏，

平均绝对误差是所有单个观测值和算术平均值的偏差的绝对值的平均。平均绝对误差可以避免误差相互抵消的问题，因而可以准确反映实际预测误差的大小

在我们拟合的回归模型中平均绝对百分比误差为0.507左右，这个结果还算理想

该例为笔者个人学习所得，若有不妥还望温和指正。