python细胞自动机及微分计算
python细胞自动机及微分计算
细胞自动机
上图是使用pygame平台来实现细胞自动机的结果展示。细胞按照生命游戏的规则进行繁衍和变化,具体规则如下:
1、如果一个细胞周围有3个细胞为活,则将细胞转换为活
2、如果一个细胞周围有2个细胞为活,则状态保持不变
3、在其他情况下,细胞都会转为死细胞
#增殖判断
def change_boxs(boxs):
# 进行一次细胞变换
# 如果一个细胞周围有3个细胞为生,则将细胞转换为生
# 如果一个细胞周围有2个细胞为生,则状态保持不变
# 在其他情况下,细胞都会转为死
x_len = len(boxs)
for x, v1 in enumerate(boxs):
y_len = len(v1)
for y, v2 in enumerate(v1):
count = 0
# 超过上限
if x == x_len-1 and y == y_len-1:
if boxs[x-1][y-1]['value'] == 1:
count += 1
if boxs[x-1][y]['value'] == 1:
count += 1
if boxs[x][y-1]['value'] == 1:
count += 1
if boxs[0][y]['value'] == 1:
count += 1
if boxs[0][y]['value'] == 1:
count += 1
if boxs[0][0]['value'] == 1:
count += 1
if boxs[x][0]['value'] == 1:
count += 1
if boxs[x-1][0]['value'] == 1:
count += 1
elif x == x_len-1:
if boxs[x-1][y-1]['value'] == 1:
count += 1
if boxs[x-1][y]['value'] == 1:
count += 1
if boxs[x-1][y+1]['value'] == 1:
count += 1
if boxs[x][y-1]['value'] == 1:
count += 1
if boxs[x][y+1]['value'] == 1:
count += 1
if boxs[0][y-1]['value'] == 1:
count += 1
if boxs[0][y]['value'] == 1:
count += 1
if boxs[0][y+1]['value'] == 1:
count += 1
pass
elif y == y_len-1:
if boxs[x-1][y-1]['value'] == 1:
count += 1
if boxs[x][y-1]['value'] == 1:
count += 1
if boxs[x+1][y-1]['value'] == 1:
count += 1
if boxs[x-1][y]['value'] == 1:
count += 1
if boxs[x+1][y]['value'] == 1:
count += 1
if boxs[x-1][0]['value'] == 1:
count += 1
if boxs[x][0]['value'] == 1:
count += 1
if boxs[x+1][0]['value'] == 1:
count += 1
else:
if boxs[x-1][y-1]['value'] == 1:
count += 1
if boxs[x-1][y]['value'] == 1:
count += 1
if boxs[x-1][y+1]['value'] == 1:
count += 1
if boxs[x][y-1]['value'] == 1:
count += 1
if boxs[x][y+1]['value'] == 1:
count += 1
if boxs[x+1][y-1]['value'] == 1:
count += 1
if boxs[x+1][y]['value'] == 1:
count += 1
if boxs[x+1][y+1]['value'] == 1:
count += 1
if count == 3:
boxs[x][y]['value'] = 1
elif count == 2:
pass
else:
boxs[x][y]['value'] = 0
微分方程1
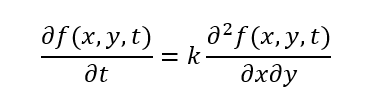
差分推导过程如下(dx = dy = dt = 1)

下述展示结果中,k取1,dt取1,dx和dy自动适应初始条件为t = 0时,f(x,y,0) = sin(x)+cos(y)。x,y取值范围分别为[-10,10],[-5,5]。
import numpy as np
import matplotlib.pyplot as plt
class UpwindMethod1:
def __init__(self, N):
self.N = N # number of nodes
self.tmax = 1
self.xmin = -10
self.xmax = 10
self.ymin = -5
self.ymax = 5
self.dt = 1 # timestep
self.initializeDomain()
self.initializeU()
self.initializeParams()
self.k = 1
def initializeDomain(self):
self.dx = (self.xmax - self.xmin) / self.N
self.x = np.arange(self.xmin - self.dx, self.xmax + (2 * self.dx), self.dx)
self.dy = (self.ymax - self.ymin)/self.N
self.y = np.arange(self.ymin - self.dy, self.ymax + (2*self.dy),self.dy)
self.x, self.y = np.meshgrid(self.x, self.y)
def initializeU(self):
u0 = np.sin(self.x) + np.cos(self.y)
self.ux = u0
self.uy = u0
self.u = self.ux.copy()
self.ut = self.uy.copy()
def initializeParams(self):
self.nsteps = round(self.tmax / self.dt)
def solve_and_plot(self):
tc = 0
fig = plt.figure()
ax = fig.add_subplot(111,projection ='3d' )
for i in range(self.N + 2):
for j in range(self.N + 2):
self.ut[i][j] = self.u[i][j] + (self.k*self.dt / (self.dx * self.dy)) * (self.ux[i][j] - self.ux[i][j - 1]) * \
(self.uy[i][j] - self.uy[i - 1][j])
self.u = self.ut.copy()
ax.plot_surface(self.x,self.y,self.ut,rstride = 1,cstride= 1, cmap = 'rainbow')
plt.grid(True)
plt.xlabel("x")
plt.ylabel("y")
plt.show()
def main():
sim = UpwindMethod1(50)
sim.solve_and_plot()
if __name__ == "__main__":
main()
微分方程2
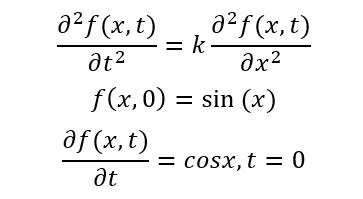
然后将上述一式展开,可得到f(x,t+dt) = 2f(x,t) -f(x,t-dt) + kdt(f(x+dx,t) - 2f(x,t) + f(x - dx,t))/dx。
三式可得(f(x,t)-f(x,t-dt))/dt = cosx,化简得到f(x,t) = f(x,t-dt) + dtcosx
结合二式,在t = 0 的初始条件下代入到一式化简式中,其后运算与方程1相同。

import numpy as np
import matplotlib.pyplot as plt
class UpwindMethod1:
def __init__(self, N):
self.N = N # number of nodes
self.tmax = 1
self.xmin = -100
self.xmax = 100
self.dt = 1 # timestep
self.initializeDomain()
self.initializeU()
self.initializeParams()
self.k = 1
def initializeDomain(self):
self.dx = (self.xmax - self.xmin) / self.N
self.x = np.arange(self.xmin - self.dx, self.xmax + (2 * self.dx), self.dx)
def initializeU(self):
u0 = np.sin(self.x)
self.ux = u0
self.u = self.ux.copy()
self.ut = self.ux.copy()
def initializeParams(self):
self.nsteps = round(self.tmax / self.dt)
def solve_and_plot(self):
tc = 0
fig = plt.figure()
# ax = fig.add_subplot(111,projection ='3d' )
for i in range(1,self.N + 1):
self.ut[i+1] = 2*self.u[i] - self.u[i-1] + (self.k*self.dt / (self.dx)) * (self.ux[i+1]-2*self.ux[i] + self.ux[i-1])
self.u = self.ut.copy()
# ax.plot_surface(self.x,self.ut,rstride = 1,cstride= 1, cmap = 'rainbow')
plt.plot(self.x[2:],self.ut[2:])
plt.grid(True)
plt.xlabel("x")
plt.ylabel("t")
plt.show()
def main():
sim = UpwindMethod1(50)
sim.solve_and_plot()
if __name__ == "__main__":
main()
反应扩散方程
通过流体方程来模拟流体运动
之前写的p5程序,根据流体运动和扩散方程来劲流体的模拟,包括受力扩散、力的传递与消失。实际上,通过速度和加速的方式来求得二阶路程时间关系可以得到流体受力和扩散方程。根据运动中的离散速度和加速度,原来的微分就变成了差分。
var N = 128;
var size;
var u = [];
var v = [];
var u_prev = [];
var v_prev = [];
var dens = [];
var dens_prev = [];
var Im = [];
var source = 10;
var diff = 0.0;
var visc = 0.0;
var dt = 0.01;
var dx = 1.0;
var vc = 5.0;
function setup() {
createCanvas(500, 500);
background(0);
stroke(0, 0, 200);
blendMode(ADD);
initSim();
}
function draw() {
background(0);
dens_prev = dens.slice();
u_prev = u.slice();
v_prev = v.slice();
add_density();
add_velocity();
vel_step();
dens_step();
vort_step();
drawDensity();
}
function initSim() {
size = (N + 2) * (N + 2);
for (var i = 0; i < size; i++) {
u[i] = 0.0;
v[i] = 0.0;
dens[i] = 0.0;
Im[i] = 0.0;
}
}
function ImageX(i, j) {
return i + (N + 2) * j;
}
function PixelX(x, y) {
return (x + width * y) * 4;
}
function normalize(x, y) {
var lenxgth = sqrt(x * x + y * y) + 1e-5;
x = x / length;
y = y / length;
}
function add_density() {
if (mouseIsPressed) {
dens[ImageX(int((N / width) * mouseX), int((N / height) * mouseY))] += source;
dens[ImageX(int((N / width) * mouseX - 1), int((N / height) * mouseY))] += source / 2;
dens[ImageX(int((N / width) * mouseX + 1), int((N / height) * mouseY))] += source / 2;
dens[ImageX(int((N / width) * mouseX), int((N / height) * mouseY - 1))] += source / 2;
dens[ImageX(int((N / width) * mouseX), int((N / height) * mouseY + 1))] += source / 2;
}
}
function add_velocity() {
var i;
if (mouseIsPressed) {
i = ImageX(int((N / width) * mouseX), int((N / height) * mouseY));
var xv = (N / width) * (mouseX - pmouseX);
var yv = (N / height) * (mouseY - pmouseY);
u[i] += xv * (2 / (abs(xv) + 1)) * 15;
v[i] += yv * (2 / (abs(yv) + 1)) * 15;
}
}
function calc_vorticity(Im0, u0, v0) {
for (var i = 1 ; i <= N ; i++) {
for (var j = 1 ; j <= N ; j++) {
Im0[ImageX(i, j)] = (u0[ImageX(i, j + 1)] - u0[ImageX(i, j - 1)]) / dx - (v0[ImageX(i + 1, j)] - v0[ImageX(i - 1, j)]) / dx;
}
}
}
function confine_vorticity(Im0, u0, v0) {
var Imgrad_x, Imgrad_y;
for (var i = 1 ; i <= N ; i++) {
for (var j = 1 ; j <= N ; j++) {
Imgrad_x = abs(Im0[ImageX(i - 1, j)]) - abs(Im0[ImageX(i + 1, j)]);
Imgrad_y = abs(Im0[ImageX(i, j - 1)]) - abs(Im0[ImageX(i, j + 1)]);
normalize(Imgrad_x, Imgrad_y);
u0[ImageX(i, j)] += Imgrad_y * Im0[ImageX(i, j)] * vc * dt;
v0[ImageX(i, j)] += -Imgrad_x * Im0[ImageX(i, j)] * vc * dt;
}
}
}
function diffuse(b, x, x0, diff0) {
var a = dt * diff0 * N * N;
for (var k = 0 ; k < 20 ; k++) {
for (var i = 1 ; i <= N ; i++) {
for (var j = 1 ; j <= N ; j++) {
x[ImageX(i, j)] = (x0[ImageX(i, j)] + a * (x[ImageX(i - 1, j)] + x[ImageX(i + 1, j)] + x[ImageX(i, j - 1)] + x[ImageX(i, j + 1)])) / (1 + 4 * a);
}
}
set_bnd(b, x);
}
}
function advect(b, d, d0, u0, v0) {
var i0, j0, i1, j1;
var x, y, s0, t0, s1, t1, dt0;
dt0 = dt * N;
for (var i = 1 ; i <= N ; i++) {
for (var j = 1 ; j <= N ; j++) {
x = i - dt0 * u0[ImageX(i, j)];
y = j - dt0 * v0[ImageX(i, j)];
if (x < 0.5)
x = 0.5;
if (x > N + 0.5)
x = N + 0.5;
i0 = int(x);
i1 = i0 + 1;
if (y < 0.5)
y = 0.5;
if (y > N + 0.5)
y = N + 0.5;
j0 = int(y);
j1 = j0 + 1;
s1 = x - i0;
s0 = 1 - s1;
t1 = y - j0;
t0 = 1 - t1;
d[ImageX(i, j)] = s0 * (t0 * d0[ImageX(i0, j0)] + t1 * d0[ImageX(i0, j1)]) + s1 * (t0 * d0[ImageX(i1, j0)] + t1 * d0[ImageX(i1, j1)]);
}
}
set_bnd(b, d);
}
function dens_step() {
diffuse(0, dens_prev, dens, diff);
advect(0, dens, dens_prev, u, v);
}
function vel_step() {
diffuse(1, u_prev, u, visc);
diffuse(2, v_prev, v, visc);
project(u_prev, v_prev, u, v);
advect(1, u, u_prev, u_prev, v_prev);
advect(2, v, v_prev, u_prev, v_prev);
project(u, v, u_prev, v_prev);
}
function vort_step() {
calc_vorticity(Im, u, v);
confine_vorticity(Im, u, v);
}
function project(u0, v0, p, div) {
var h = 1.0 / N;
for (var i = 1 ; i <= N ; i++) {
for (var j = 1 ; j <= N ; j++) {
div[ImageX(i, j)] = 0.5 * h * (u0[ImageX(i + 1, j)] - u0[ImageX(i - 1, j)] + v0[ImageX(i, j + 1)] - v0[ImageX(i, j - 1)]);
p[ImageX(i, j)] = 0;
}
}
set_bnd(0, div);
set_bnd(0, p);
var residual;
for (var k = 0 ; k < 100 ; k++) {
for (i = 1 ; i <= N ; i++) {
for (j = 1 ; j <= N ; j++) {
residual = -4 * p[ImageX(i, j)] + p[ImageX(i - 1, j)] + p[ImageX(i + 1, j)] + p[ImageX(i, j - 1)] + p[ImageX(i, j + 1)] - div[ImageX(i, j)];
p[ImageX(i, j)] += residual * (1.7 / 4);
}
}
set_bnd(0, p);
}
for (i = 1 ; i <= N ; i++) {
for (j = 1 ; j <= N ; j++) {
u0[ImageX(i, j)] -= 0.5 * (p[ImageX(i + 1, j)] - p[ImageX(i - 1, j)]) / h;
v0[ImageX(i, j)] -= 0.5 * (p[ImageX(i, j + 1)] - p[ImageX(i, j - 1)]) / h;
}
}
set_bnd(1, u0);
set_bnd(2, v0);
}
function set_bnd(b, x) {
for (var i = 1 ; i <= N ; i++) {
x[ImageX(0, i)] = b == 1 ? -x[ImageX(1, i)] : x[ImageX(1, i)];
x[ImageX(N + 1, i)] = b == 1 ? -x[ImageX(N, i)] : x[ImageX(N, i)];
x[ImageX(i, 0)] = b == 2 ? -x[ImageX(i, 1)] : x[ImageX(i, 1)];
x[ImageX(i, N + 1)] = b == 2 ? -x[ImageX(i, N)] : x[ImageX(i, N)];
}
x[ImageX(0, 0)] = 0.5 * (x[ImageX(1, 0)] + x[ImageX(0, 1)]);
x[ImageX(0, N + 1)] = 0.5 * (x[ImageX(1, N + 1)] + x[ImageX(0, N)]);
x[ImageX(N + 1, 0)] = 0.5 * (x[ImageX(N, 0)] + x[ImageX(N + 1, 1)]);
x[ImageX(N + 1, N + 1)] = 0.5 * (x[ImageX(N, N + 1)] + x[ImageX(N + 1, N)]);
}
function drawDensity() {
var dx, dy, ddx, ddy;
var df, di;
loadPixels();
for (var x = 0; x < width; x++) {
for (var y = 0; y < height; y++) {
dx = (N / width) * x;
ddx = dx - int(dx);
dy = (N / height) * y;
ddy = dy - int(dy);
df = (dens[ImageX(floor(dx), floor(dy))] * (1.0 - ddx) + dens[ImageX(ceil(dx), floor(dy))] * ddx) * (1.0 - ddy) + (dens[ImageX(floor(dx), ceil(dy))] * (1.0 - ddx) + dens[ImageX(ceil(dx), ceil(dy))] * ddx) * ddy;
di = int(df * 255);
if (di < 0)
di = 0;
if (di > 255)
di = 255;
pixels[PixelX(x, y)] = pixels[PixelX(x, y)] * (1 - df) + di * df;
pixels[PixelX(x, y) + 1] = 0;
pixels[PixelX(x, y) + 2] = 0;
pixels[PixelX(x, y) + 3] = 255;
}
}
updatePixels();
}