全链接神经网络python简单实现

什么是全链接神经网络(full connected, FC)？

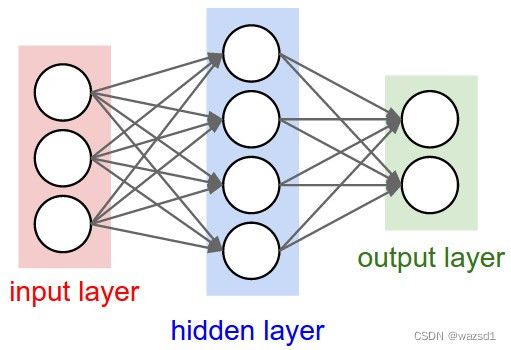
借用此图来直观的表示一下。

规则如下：

• 神经元按照层来布局。最左边的层叫做输入层，负责接收输入数据；最右边的层叫输出层，我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层，因为它们对于外部来说是不可见的。
• 同一层的神经元之间没有连接。
• 第N层的每个神经元和第N-1层的所有神经元相连(这就是full connected的含义)，第N-1层神经元的输出就是第N层神经元的输入。
• 每个连接都有一个权值。

 全链接神经网络是神经网络的基础结构，很多其它结构的神经网络，比如卷积神经网络(CNN)、循环神经网络(RNN)，他们都是以全链接神经网络为基础形成的不同的连接规则网络。

对于全链接神经网络很多人都抽象的说就是左边输入，中间计算，右边输出的结构，如：

 简单的来说的化，好像确实是这么回事。

前向计算、反向传播应该是对训练全链接神经网络最合适的说辞，前向计算指的是计算出隐藏层和输出层各节点的值，反向传播说的是误差项的传播。反向传播算法是目前用来训练人工神经网络（Artificial Neural Network，ANN）的最常用且最有效的算法，对于全链接神经网络的契合度很高。

全链接神经网络中神经元节点的激活函数往往选择为sigmoid函数或tanh函数。这里我们选择sigmoid函数：

其导数为：

 接下来我们介绍下前向计算和反向传播的具体过程：

 前向计算：

以单个神经元为单位下：

 

 矩阵形式的表示：

 反向传播算法(Back Propagation)：误差项的传播

其中 就是节点 i 的误差项。下面给出公式描述过程骨架：

 详细的解释可以参考：零基础入门深度学习(3) - 神经网络和反向传播算法 - 作业部落 Cmd Markdown 编辑阅读器

 下面是代码的实现：

import numpy as np

# question: 数据的归一化处理可不可以添加进入， 初始数据的样例, 初始权值的选取
# 本身程序的错误:解决-->类中使用的都是实例方法，规定必须含有一个位置参数self

class Begin:
    def __init__(self, x, wa, wb, y, b1, b2, n): # 前向计算所需要的属性有:x最初输入，wa、wb最初权重  后向传播所需要的属性有:y
        self.x = x
        self.wa = wa
        self.wb = wb
        self.y = y
        self.n = n
        self.b1 = b1
        self.b2 = b2

    # 前向计算部分
    def hide_output(self, x, wa, b1):  # 隐藏层输出值函数
        return sigmoid(np.dot(x, wa) + b1) # 返回的是隐藏层的ai矩阵

    def out_output(self, a2, wb, b2):  # 这里的x对应着隐藏层的输出矩阵
        return sigmoid(np.dot(a2, wb) + b2) # 返回的是隐藏层的ai矩阵
    
    def count_front(self):  # 计算出预测值和隐藏层节点的值
        # 得到各神经元的结果， 前向计算完成
        self.wa = np.transpose(self.wa)
        a1 = self.hide_output(self.x, self.wa, self.b1) # 得到1x4
        self.wa = np.transpose(self.wa)

        self.wb = np.transpose(self.wb)
        t = self.out_output(a1, self.wb, self.b2)  # 得到的预测输出值   -->  矩阵相乘对形势有要求: 如果存在偏置，那么应该a1还要加上偏执对应的1
        self.wb = np.transpose(self.wb)
        # print('a1的矩阵形式:', a1.shape, '\nt的矩阵形式:', t.shape)
        return a1, t


    def hide_deviation(self, a1, det, wb):  # 隐藏层误差函数
        return a1 * (1 - a1) * np.dot(det, wb)

    def out_deviation(self, y, t):  # 输出层误差函数
        return t * (1 - t) * (y - t)
    
    def count_back(self, t, a1):
        # 后向传输：先做一次迭代

        # 输出层节点误差
                    # 问题是矩阵的运算出现知识短缺：dot得到的都是数字，而不是理想的矩阵!!!  问题解决
                # # 模拟一下矩阵对公式的适用性
                # y = np.array([[1, 2, 3, 4]])
                # t = np.array([[4, 3, 2, 1]])
                # #      问题：矩阵无法满足我们想的对应元素乘法好像
                # # 问题解决：当*表示的是两个np.array相乘时，表示矩阵对应元素的相乘;   当*表示的是两个np.matrix表示的是普通的矩阵乘法
                # # print(y * t)
                # det = y * (1 - y) * (t - y)
                # print(det)
        det = self.out_deviation(self.y, t)
        # print('输出层节点误差:\n', det, '\ndet的形式:', det.shape)

        # 隐藏层节点误差
            # 问题：偏置权重有没有？公式的计算有没有影响，例如矩阵的计算时用到那个a的矩阵？
            # 误差值与偏置没有关系，公式中并没有偏置的影响,偏置影响到的是输出值的求解和迭代

        det1 = self.hide_deviation(a1, det, wb) # 偏置对的是节点吗:是的，每个节点都一个偏置,就算是输出层节点也有偏置
        # print('隐藏层节点误差:\n', det1, '\ndet1的形式:', det1.shape)
        return det1, det

    def mount(self):
        a1, t = self.count_front()
        det1, det = self.count_back(t, a1)
        return det1, det, a1

# 训练函数
def train(det1, det, a1, n, wb, wa, x, b1, b2):
    det1 = np.transpose(det1)
    wa = wa + n * np.dot(det1, x)
    print('wa的迭代变化矩阵:\n', np.dot(det1, x))
    print('迭代后的wa为:\n', wa)
    det1 = np.transpose(det1)

    det = np.transpose(det)
    wb = wb + n * np.dot(det, a1)
    print('wb的迭代变化矩阵:\n', np.dot(det, a1))
    print('迭代后的wb为:\n', wb)
    det = np.transpose(det)

    b1 = b1 + n * det1
    b2 = b2 + n * det

    return wa, wb, b1, b2


# 迭代函数
def iterate(wa, wb, b1, b2, n, e):

    # j = 0
    while True:

        boolx = True
        # 从文件导入数据, 这个前提是基于知道数据存储的样式
        datafile = r'./BP/train_data.txt'
        with open(datafile, encoding='utf-8') as lines:
            for line in lines:
                line = line[:-1]  # 去除换行符
                x1, x2, x3, y1, y2 = line.split(' ')  # 注意最后一行数据必须有换行符
                x1 = float(x1)
                x2 = float(x2)
                x3 = float(x3)
                y1 = float(y1)
                y2 = float(y2)
                x = np.array([[x1, x2, x3]])
                y = np.array([[y1, y2]])
                print('x矩阵为:', x, '\ny矩阵为:', y)
                
                # 每次都要前向计算和后向传播
                one = Begin(x, wa, wb, y, b1, b2, n)
                det1, det, a1 = one.mount()

                # j += 1
                # print(j)

                if det[0][1] < e and det[0][0] < e: # 输出层误差几乎等于0，则退出迭代循环
                    boolx = False
                    break

                # 训练更新权值
                wa, wb, b1, b2 = train(det1, det, a1, n, wb, wa, x, b1, b2)

                # 检测
                print('det为:\n', det)

        if boolx == False:
            print('最终Det为:\n', det)
            print('隐藏层节点的权重wa:', wa, '\n隐藏层节点的权重b1:\n', b1, '\n输出层节点的权重wb:\n', wb, '\n输出层节点的权重b2:\n', b2)
            break

        # if j >=1000:
        #     print('隐藏层节点的权重wa:', wa, '\n隐藏层节点的权重b1:\n', b1, '\n输出层节点的权重wb:\n', wb, '\n输出层节点的权重b2:\n', b2)
        #     break

# 神经网络激活函数为sigmoid函数, 采用numpy方法
def sigmoid(x):
    z = np.exp(-x)
    sig = 1 / (1 + z)

    return sig

# 初始节点权重定义
# w4, w5, w6, w7, w8, w9都不是矩阵， wa, wb才是矩阵，这和矩阵在python中的定义有关
w4 = np.array([0.4, 0.4, 0.2])  # 隐藏层a4对输入层的权值，无偏置
w5 = np.array([0.3, 0.2, 0.5])  # 隐藏层a5对输入层的权值，无偏置
w6 = np.array([0.6, 0.3, 0.1])  # 隐藏层a6对输入层的权值，无偏置
w7 = np.array([0.3, 0.4, 0.3])  # 隐藏层a7对输入层的权值，无偏置

w8 = np.array([0.2, 0.3, 0.4, 0.1]) # 输出层y1对隐藏层的权值，无偏置
w9 = np.array([0.5, 0.1, 0.3, 0.1]) # 输出层y2对隐藏层的权值，无偏置

wa = np.array([w4, w5, w6, w7]) # 输入隐藏层间的的权重  
wb = np.array([w8, w9]) # 输出隐藏层间的权重
print('wa的矩阵形式:', wa.shape, '\nwb的矩阵形式:', wb.shape)

b1 = np.array([[0, 0.2, 0.5, 0.3]]) # a4--a7的偏置
b2 = np.array([[1, 0]])  # a8-a9的偏置

e = 0.001
n = 0.5

# 迭代
iterate(wa, wb, b1, b2, n, e)

 代码写的很简略，对导入数据的归一化并未加入，而且初始数据其实是随便写的，文件如下图：

 最后的结果也并没有向线性回归时那样规整，因为初始数据少而且粗略，所以代码中学习率这种要求细致的参数也没加入什么操作。

 参考：零基础入门深度学习(3) - 神经网络和反向传播算法 - 作业部落 Cmd Markdown 编辑阅读器